12個の椅子の1つにダイヤモンドが縫い付けられる確率は0.9です。 椅子が順番に開かれ、現在の椅子にダイヤモンドが存在しない場合にのみ次の移動が行われるという仮定の下で、ダイヤモンドが列椅子の12番目にある確率を見つけます。
近い将来、正確な数値を無視して、ダイヤモンドがpに等しくなる確率と、椅子の数-nを入れてみましょう。
この問題の正しい解決策を知りたいですか? 猫へようこそ!
それでは、遠くから始めましょう。 まず、ダイヤモンドが最初の椅子にいる確率を見つけます。 合計確率の式を使用します。 見つける
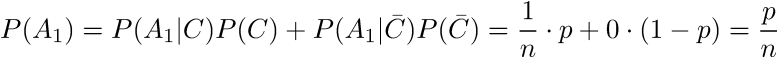
椅子を同時にチェックするのではなく、順番にチェックするため、最初の椅子に何もない場合にのみ2番目の椅子を開きます。
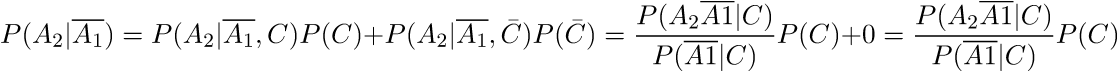
確率の積の規則に従って、結果の分数の分子を開示したい誘惑がありますが、これはできません。 椅子を順番にチェックします。つまり、イベントは独立していません。 ダイヤモンドは、配置された場合、12の椅子のいずれかに等しくなる可能性があるため、イベントの確率は次のようになります。
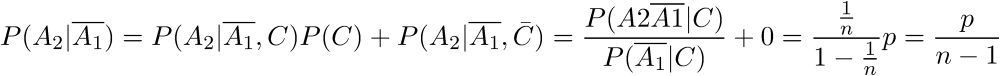
新しい反復を作成すると、次のようになります。
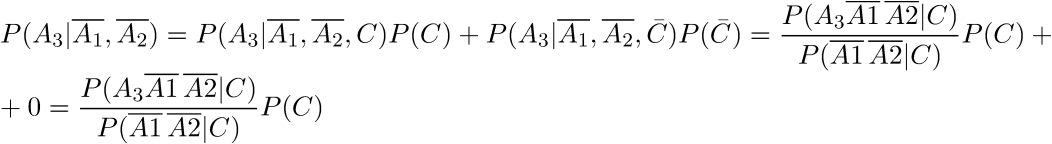
繰り返しますが、分母のイベントは独立ではなく、確率積の式を適用する権利はありませんが、確率の加算式を使用できます。
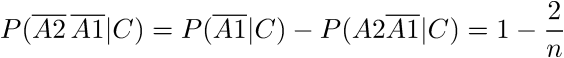
その結果、次の式が得られます。

これで、k番目の椅子にダイヤモンドが縫い付けられる確率の最終式は次の形式になることがわかります。
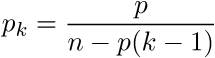
初期値を代入します:p = 0.9およびn = 12。 その結果、0。(428571)または42.85%の答えが得られます。
計算の誤りに気づいたユーザーmayorovpに感謝します。 私は心から、最も明るい人々だけが彼の方法で会うことを望みます。 よろしく、ProPupil。