この投稿では、地理空間インデックス、つまり、 R *ツリーなどのデータ構造と、最初のプロジェクトの実装方法について説明します。
それでは始めましょう。 卒業後すぐに、私は車のGPS監視サービスを提供するオフィスを持っている教師から申し出を受けましたが、それを受け入れました。 ここにある! 最後に、本当に興味深いプロジェクト! 私の喜びと熱意には限界がありませんでした。 私に与えられた最初のタスクには、次の文言がありました。
マイレージ、車の使用済み燃料などに関するレポートに加えて、ベクトルマップが表示され、これらの同じ車の位置がリアルタイムで表示され、車の動きの履歴やあらゆる種類のグッズが表示されるデスクトップアプリケーションがあります。 現在、これらはすべて正しくなく、非効率的に機能しています。 誰もそれを正しく実装する方法を知りません。 書き換える必要がある...
私の手には、160,000行分のアプリケーションのソースコードが渡されました。 ドキュメントなし、何もない。 情報の唯一の情報源は、これらのまさに教師であり、「Vasyaの要請でn * xを削除しました」という計画のソースコード内のまれなコメントでした。 このプロジェクトは10年以上前に行われ、オフィスは非常に忠実で柔軟で、文書化されていないあらゆる種類のウィッシュリストとホイッスルをほぼすぐに顧客の要求に迅速に対応します。 ものすごい過失! しかし、そのようなプロジェクトは、他人のコードを解析するスキルを高めるのに役立ちます。
まあ、タスクが設定された、仕事のための材料がありました。 コードをざっと調べ、質問をして、当時の現状を少し明らかにしました。
- マップは、これらのポイントへのリンクを持つポイントとオブジェクトの配列です
- 画面領域にヒットするオブジェクトは、徹底的な検索によって決定されます。
- オブジェクトを表示するかどうかは、画面上のオブジェクトのサイズを計算することにより「オンザフライ」で決定されました(1ピクセルサイズの家の表示にシステムリソースを費やすことは意味がありません)
小さいサイズの地図(都市、地区)の描画は許容範囲でした。 合計数百万のポイントで構成される数十万のベクトルオブジェクトを含む地域\国のサイズのマップを読み込むときに何が起こったのか、想像できます。 グーグルでこのトピックに関する多くの資料を読んで、すべてを「正しく実行する」ための2つのオプションを自分で特定しました。
- マップの領域全体を固定サイズの正方形に分割し、ジョイントに当たるオブジェクトを分割し、各オブジェクトに正方形のインデックスを割り当て、データを並べ替えて、必要なオブジェクトを外出先で計算します。
- Rツリーを使用します。
少し考えてから、最初のオプションを捨てました 特定の数のスケールレベルに取り付けて、それぞれのグリッドを構築する必要があります。 2番目のオプションには、無制限のスケーリングという利点があり、一般的にはより普遍的であると思われました。 車輪を再発明しないために、Delphiで既存のライブラリを検索することにしました。 プロジェクトはそれに書かれていました。 ライブラリが見つからなかったため、自分でインデックス作成を実装することにしました。
Rツリーとは何ですか? この構造は、空間データにインデックスを付けるためにアントニングットマンによって提案されたもので、バランスの取れたツリーであり、経験的観察に基づいて開発されました。 ツリーは、スペースを多くのネストされた長方形に分割します。 各ツリーノードには、最小( minCount )および最大( maxCount )のオブジェクト数があります。 ツリー構築アルゴリズムを正しく動作させるには、 2 <= minCount <= maxCount / 2であることが必要です。 各オブジェクトには、独自の境界矩形-MBR (最小境界矩形)があります。 MBRノードは、子ノード\オブジェクトの長方形を記述する長方形です。
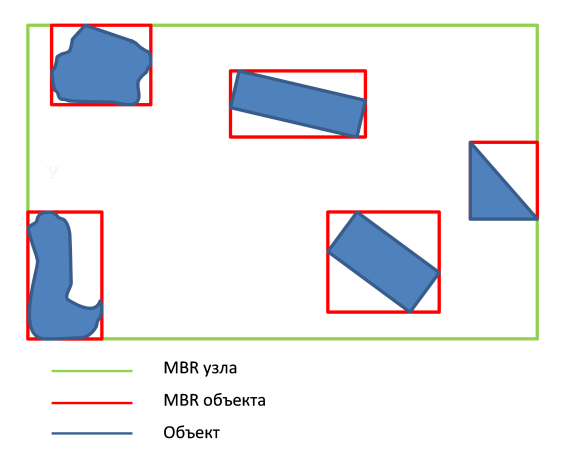
ツリーは、オブジェクトを交互に挿入することで構築されます。 ノードがオーバーフローすると、ノードが分割され、必要に応じてすべての親ノードが分割されます。 特定のデータ構造に対する検索クエリの有効性は、いくつかの基準に依存します。
- MBRノードの領域を最小化する(オブジェクト間の空きスペースを最小化する);
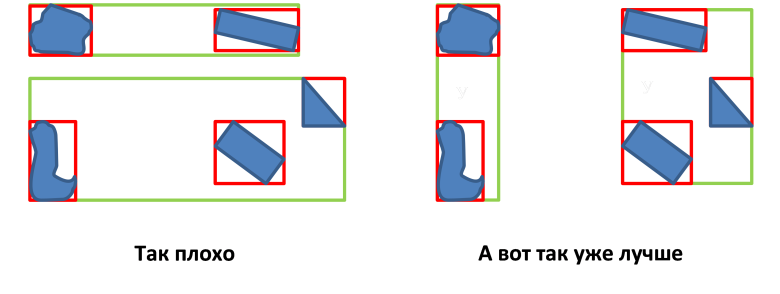
- MBRノードの重複領域の面積の最小化。
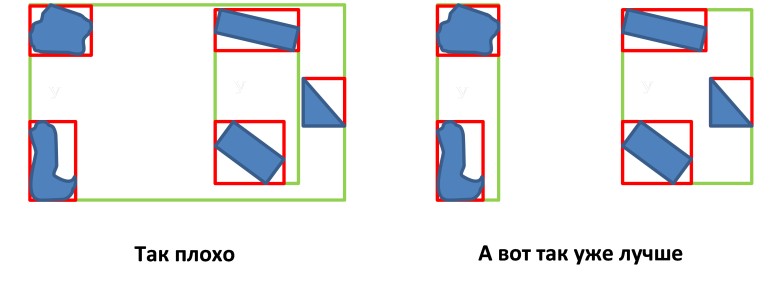
- MBRノードの境界線を最小化します。
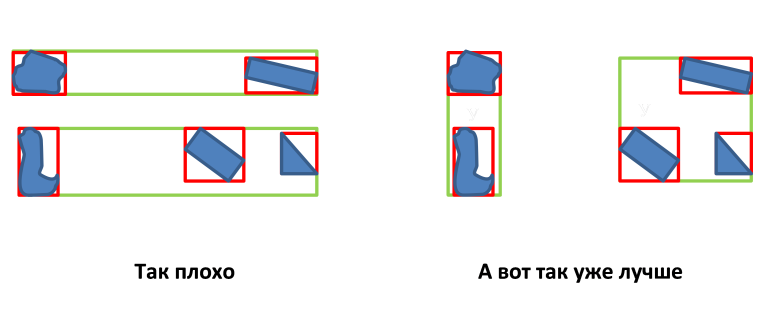
Rツリーにはさまざまなタイプがあり、最終ノードの選択と混雑したノードの分割のみが異なります。
なぜR * -treeを選択したのですか? Antonin Gutmann(R-trees)が私の主観的な評価で提案した古典的なアプローチは、実際のプロジェクトでの使用にはまったく不適切です。 例として、ドイツの郵便局用に構築されたWikipediaの資料、すなわちRツリーを引用します。
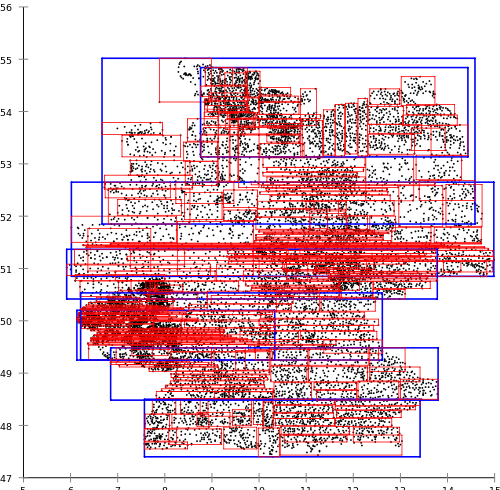
同時に、Norbert Beckmann、Hans-Peter Kriegel、Ralph Schneider、およびBernhard Seegerによって提案されたR *ツリーアルゴリズムは、次の結果をもたらします。
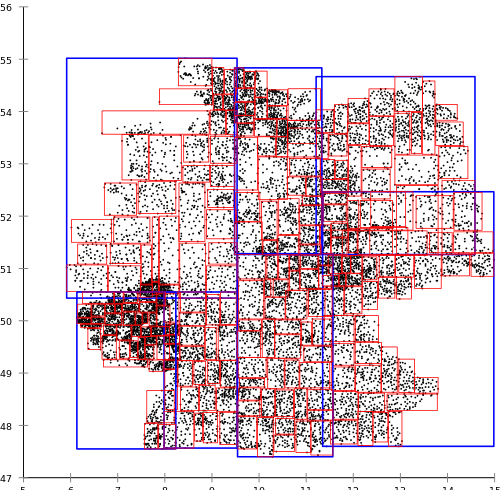
R * -treeは、作成するのにより多くのリソースを消費しますが、通常のR-treeよりも検索クエリの結果が優れています。
挿入がどのように発生するかを検討してください。ブランチ(サブツリー)/ノードを選択するアルゴリズムと、ノードがいっぱいになったときにノードを分割するアルゴリズムが含まれています。
サブツリー選択アルゴリズム(chooseSubtree)
1.ルートノードとしてNを設定します 2. Nがエンドノードの場合、Nを返します 3.その他 4. Nの子ノードが最終ノード(リーフ)である場合、 5. MBRが挿入時のオーバーラップの最小増加を必要とする子ノードNを選択します オブジェクトからノード 6.オーバーラップの増加が最小のノードが複数ある場合は、それらからノードを選択します 面積の最小の増加が必要です 7.面積の増加が最小のノードが複数ある場合は、それらからノードを選択します 最小面積で 8.それ以外の場合 9. MBRで面積の増加が最小である子ノードNを選択します 10.面積の増加が最小のノードが複数ある場合は、面積が最小のノードを選択します 11. Nを選択したノードに設定します。 12.手順2から繰り返します。
ノード分割アルゴリズム(splitNode)
分割オプションを見つけるために、R *-ツリーは次の方法を使用します。ノードは、左右の境界に沿った各座標軸に沿ってソートされます。 ソートされたバージョンごとに、ノードは2つのグループに分割されるため、 k = [1 ...(maxCount-2 * minCount + 2)]の場合、最初のグループには(minCount-1)+ k番目のノードが残ります。 そのような分布ごとに、次の指標が計算されます。
- エリア:エリア=エリア(最初のグループのMBR)+エリア(2番目のグループのMBR)
- 境界:マージン=マージン(最初のグループのMBR)+マージン(2番目のグループのMBR)
- オーバーラップ:オーバーラップ=エリア(最初のグループのMBR second 2番目のグループのMBR)
最適な分布は、次のアルゴリズムによって決定されます。
1. chooseSplitAxisを呼び出して、分布が発生する軸を決定します。 2. chooseSplitIndexを呼び出して、選択した軸上の最適な分布を決定します 3.オブジェクトを2つのノードに割り当てます
chooseSplitAxis
1.各軸について 2.ノードを左、次にMBRの右境界線で並べ替えます。 上記のようにノードを配布し、S-各配布のすべての境界の合計を計算します。 3. Sが最小の軸を選択します。
chooseSplitIndex
1.選択した軸に沿って、最小オーバーラップパラメーターを持つ分布を選択します 2.最小オーバーラップパラメーターを持つ分布が複数ある場合は、分布を選択します 最小面積で。
実際には挿入自体(insertObject)
1. chooseSubStreeを呼び出し、ルートノードを引数として渡してNノードを決定し、 オブジェクトEの挿入が発生する場所 2. Nのオブジェクトの数がmaxCountより小さい場合、 3. EをNに挿入します 4. Nおよびそのすべての親ノードのMBRを更新します 5.それ以外の場合、NおよびEに対してsplitNodeを呼び出します。
記事の R *ツリーの著者は、この構造の最高のパフォーマンスはminCount = maxCount * 40%で達成されると主張しています。
以上です。 私たちのツリーは構築されており、特定のエリアで適切なオブジェクトを見つけることは難しくありません。
特定のエリアでオブジェクトを見つけるためのアルゴリズム(findObjectsInArea)
1.現在のノードNが有限の場合、 2.ノードNの各子オブジェクトEについて、決定します 3. Eが検索領域と交差する場合、検索結果RにEを追加します。 4.それ以外の場合 5.ノードNの各子ノードnについて、決定します 6. nが検索領域と交差する場合、nに対してfindObjectsInAreaを呼び出します
次に、単に
findObjectsInArea
を呼び出して、ルートノードと検索領域を渡します。
基本的なアルゴリズムの動作をより明確に示すために、コードを見てみましょう。
ソルスキ
// R*-tree unit RStar_tree; interface uses Windows, SysUtils, Math; const MAX_M = 16; // MIN_M = Round(MAX_M * 0.4); // type TObjArr = array of Integer; // TAxis = (X, Y); // chooseSplitAxis - TBound = (Left, Right); // (\) TGpsPoint = record // GPS (X = lon\Y = lat) X, Y: Double; end; TMBR = record // \\ MBR = Minimum Bounding Rectangle Left, Right: TGpsPoint; // left - right - end; TRObject = record // R-. mbr: TMBR; // idx: Integer; // , end; TRNode = class // private fmbr: TMBR; // FParent: Integer; // , - FChildren: array of Integer; // FObjects: array of TRObject; // . ( () (, , ) FisLeaf: Boolean; // () FLevel: Integer; // (0=) protected function getIsLeaf: Boolean; // FisLeaf function getChild(Index: Integer): Integer; // function getObject(Index: Integer): TRObject; // procedure setChild(Index: Integer; node_id: Integer); // procedure setObject(Index: Integer; obj: TRObject); // procedure setParent(parent_id: Integer); // - Procedure copy(node: TRNode); // Procedure clearObjects(); // Procedure clearChildren(); // public constructor Create; overload; constructor Create(node: TRNode); overload; destructor Destroy; override; property mbr: TMBR read fmbr write fmbr; // property isLeaf: Boolean read FisLeaf; // property Children[Index: Integer]: Integer read getChild write setChild; // property Objects[Index: Integer]: TRObject read getObject write setObject; // property Parent: Integer read FParent write setParent; // property Level: Integer read FLevel write FLevel; // function isIntersected(mbr1, mbr2: TMBR): Boolean; overload; // mbr1, mbr2 function isIntersected(mbr: TMBR): Boolean; overload; // MBR mbr function Overlap(mbr_ovrl: TMBR): Double; // MBR function Area: Double; overload; // MBR function Area(mbr: TMBR): Double; overload; // MBR function margin: Double; // MBR end; TRtree = class // private FNodeArr: array of TRNode; // FRoot: Integer; // FHeight: Integer; // Procedure QuickSort(var List: array of TRObject; iLo, iHi: Integer; axe: TAxis; bound: TBound); overload; // MBR. axe - , bound - (/) procedure QuickSort(var List: array of Integer; iLo, iHi: Integer; axe: TAxis; bound: TBound); overload; // MBR. axe - , bound - (/) Procedure splitNodeRStar(node_id: Integer; obj: TRObject); overload; // 2 R*-tree (page 325:: The R*-tree: An Efficient and Robust Access Method for Points and Rectangles+) node_id = obj = Procedure splitNodeRStar(splited_Node_Id, inserted_Node_Id: Integer); overload; // 2 R*-tree (page 325:: The R*-tree: An Efficient and Robust Access Method for Points and Rectangles+) splited_Node_Id = , inserted_Node_Id = Procedure updateMBR(node_id: Integer); overload; // MBR Procedure updateMBR(node: TRNode); overload; // MBR Procedure chooseSubtree(obj: TRObject; var node_id: Integer); // node_id obj. function chooseSplitAxis(obj: TRObject; node_id: Integer): TAxis; overload; // ( R*-tree) function chooseSplitAxis(nodeFather, nodeChild: Integer): TAxis; overload; // ( R*-tree) Procedure findObjectsInArea(mbr: TMBR; node_id: Integer; var obj: TObjArr); overload; // mbr function isRoot(node_id: Integer): Boolean; // node_id function newNode(): Integer; // . protected public constructor Create; destructor Destroy; override; Procedure insertObject(obj: TRObject); // Procedure findObjectsInArea(mbr: TMBR; var obj: TObjArr); overload; // mbr. (. .. , ) property Height: Integer read FHeight; // end; function toRObject(lx, ly, rx, ry: Double; idx: Integer): TRObject; overload; function toRObject(mbr: TMBR; idx: Integer): TRObject; overload; implementation function toRObject(lx, ly, rx, ry: Double; idx: Integer): TRObject; begin Result.mbr.Left.X := Min(lx, rx); Result.mbr.Left.Y := Min(ly, ry); Result.mbr.Right.X := Max(lx, rx); Result.mbr.Right.Y := Max(ly, ry); Result.idx := idx; end; function toRObject(mbr: TMBR; idx: Integer): TRObject; begin Result.mbr := mbr; Result.idx := idx; end; { TRNode } function TRNode.Area: Double; begin Result := (fmbr.Right.X - fmbr.Left.X) * (fmbr.Right.Y - fmbr.Left.Y); end; function TRNode.Area(mbr: TMBR): Double; begin Result := (mbr.Right.X - mbr.Left.X) * (mbr.Right.Y - mbr.Left.Y); end; procedure TRNode.clearChildren; begin SetLength(FChildren, 0); end; procedure TRNode.clearObjects; begin FisLeaf := False; SetLength(FObjects, 0); end; procedure TRNode.copy(node: TRNode); var i: Integer; begin SetLength(FObjects, Length(node.FObjects)); SetLength(FChildren, Length(node.FChildren)); if Length(FObjects) > 0 then begin for i := 0 to High(node.FObjects) do begin FObjects[i].idx := node.FObjects[i].idx; FObjects[i].mbr.Left.X := node.FObjects[i].mbr.Left.X; FObjects[i].mbr.Left.Y := node.FObjects[i].mbr.Left.Y; FObjects[i].mbr.Right.X := node.FObjects[i].mbr.Right.X; FObjects[i].mbr.Right.Y := node.FObjects[i].mbr.Right.Y; end; FisLeaf := True; end else begin for i := 0 to High(node.FChildren) do begin Children[i] := node.Children[i]; end; FisLeaf := False; end; fmbr.Left.X := node.fmbr.Left.X; fmbr.Left.Y := node.fmbr.Left.Y; fmbr.Right.X := node.fmbr.Right.X; fmbr.Right.Y := node.fmbr.Right.Y; FParent := node.Parent; FLevel := node.Level; end; constructor TRNode.Create(node: TRNode); begin Create; FParent := -10; copy(node); end; constructor TRNode.Create; begin inherited; FParent := -10; end; destructor TRNode.Destroy; begin SetLength(FObjects, 0); SetLength(FChildren, 0); inherited; end; function TRNode.getChild(Index: Integer): Integer; begin if High(FChildren) >= Index then begin Result := FChildren[Index]; end; end; function TRNode.getIsLeaf: Boolean; begin if Length(FObjects) > 0 then Result := True else Result := False; end; function TRNode.getObject(Index: Integer): TRObject; begin if High(FObjects) >= Index then begin Result := FObjects[Index]; end; end; function TRNode.isIntersected(mbr: TMBR): Boolean; begin Result := False; if (fmbr.Left.X <= mbr.Right.X) and (fmbr.Left.Y <= mbr.Right.Y) then begin if (fmbr.Right.X >= mbr.Left.X) and (fmbr.Right.Y >= mbr.Left.Y) then begin Result := True; end; end; end; function TRNode.margin: Double; begin Result := ((fmbr.Right.X - fmbr.Left.X) + (fmbr.Right.Y - fmbr.Left.Y)) * 2; end; function TRNode.Overlap(mbr_ovrl: TMBR): Double; var X, Y: Double; begin X := Min(mbr_ovrl.Right.X, fmbr.Right.X) - Max(mbr_ovrl.Left.X, fmbr.Left.X); if X <= 0 then begin Result := 0; Exit; end; Y := Min(mbr_ovrl.Right.Y, fmbr.Right.Y) - Max(mbr_ovrl.Left.Y, fmbr.Left.Y); if Y <= 0 then begin Result := 0; Exit; end; Result := X * Y; end; function TRNode.isIntersected(mbr1, mbr2: TMBR): Boolean; begin Result := False; if (mbr1.Left.X <= mbr2.Right.X) and (mbr1.Left.Y <= mbr2.Right.Y) then begin if (mbr1.Right.X >= mbr2.Left.X) and (mbr1.Right.Y >= mbr2.Left.Y) then begin Result := True; end; end; end; procedure TRNode.setChild(Index, node_id: Integer); begin if High(FChildren) >= Index then begin FChildren[Index] := node_id; FisLeaf := False; end else begin if ((Index) <= (MAX_M - 1)) and (Index >= 0) then begin SetLength(FChildren, Index + 1); FChildren[Index] := node_id; FisLeaf := False; end; end; end; procedure TRNode.setObject(Index: Integer; obj: TRObject); begin if High(FObjects) >= Index then begin FObjects[Index] := obj; FisLeaf := True; end else begin if ((Index) <= (MAX_M - 1)) and (Index >= 0) then begin SetLength(FObjects, Index + 1); FObjects[Index] := obj; FisLeaf := True; end; end; end; procedure TRNode.setParent(parent_id: Integer); begin if parent_id >= 0 then FParent := parent_id; end; { TRtree } function TRtree.chooseSplitAxis(obj: TRObject; node_id: Integer): TAxis; var arr_obj: array of TRObject; i, j, k, idx: Integer; node_1, node_2: TRNode; perimeter_min, perimeter: Double; begin SetLength(arr_obj, MAX_M + 1); if not FNodeArr[node_id].isLeaf then Exit; for i := 0 to High(FNodeArr[node_id].FObjects) do begin arr_obj[i] := FNodeArr[node_id].FObjects[i]; end; arr_obj[ High(arr_obj)] := obj; node_1 := TRNode.Create; node_2 := TRNode.Create; perimeter_min := 999999; for i := 0 to 1 do // begin perimeter := 0; for j := 0 to 1 do // () begin node_1.clearObjects; node_2.clearObjects; QuickSort(arr_obj, 0, High(arr_obj), TAxis(i), TBound(j)); for k := 1 to MAX_M - MIN_M * 2 + 2 do // begin idx := 0; while idx < ((MIN_M - 1) + k) do // (MIN_M - 1) + k begin node_1.Objects[idx] := arr_obj[idx]; idx := idx + 1; end; for idx := idx to High(arr_obj) do // begin node_2.Objects[idx - ((MIN_M - 1) + k)] := arr_obj[idx]; end; updateMBR(node_1); updateMBR(node_2); perimeter := perimeter + ((node_1.mbr.Right.X - node_1.mbr.Left.X) * 2 + (node_2.mbr.Right.Y - node_2.mbr.Left.Y) * 2); end; end; if perimeter <= perimeter_min then begin Result := TAxis(i); perimeter_min := perimeter; end; perimeter := 0; end; SetLength(arr_obj, 0); FreeAndNil(node_1); FreeAndNil(node_2); end; function TRtree.chooseSplitAxis(nodeFather, nodeChild: Integer): TAxis; var arr_node: array of Integer; i, j, k, idx: Integer; node_1, node_2: TRNode; perimeter_min, perimeter: Double; begin SetLength(arr_node, MAX_M + 1); for i := 0 to High(FNodeArr[nodeFather].FChildren) do begin arr_node[i] := FNodeArr[nodeFather].FChildren[i]; end; arr_node[ High(arr_node)] := nodeChild; perimeter_min := 999999; node_1 := TRNode.Create; node_2 := TRNode.Create; for i := 0 to 1 do // begin perimeter := 0; for j := 0 to 1 do // () begin node_1.clearChildren; node_2.clearChildren; QuickSort(arr_node, 0, High(arr_node), TAxis(i), TBound(j)); for k := 1 to MAX_M - MIN_M * 2 + 2 do // begin idx := 0; while idx < ((MIN_M - 1) + k) do // (MIN_M - 1) + k begin node_1.Children[idx] := arr_node[idx]; idx := idx + 1; end; for idx := idx to High(arr_node) do // begin node_2.Children[idx - ((MIN_M - 1) + k)] := arr_node[idx]; end; updateMBR(node_1); updateMBR(node_2); perimeter := perimeter + node_1.margin + node_2.margin; end; end; if perimeter <= perimeter_min then begin Result := TAxis(i); perimeter_min := perimeter; end; perimeter := 0; end; FreeAndNil(node_1); FreeAndNil(node_2); SetLength(arr_node, 0); end; procedure TRtree.chooseSubtree(obj: TRObject; var node_id: Integer); var i, id_child: Integer; min_overlap_enlargement: Double; // Overlap_enlargement: Double; area_enlargement: Double; idChild_overlap: array of Integer; { . , , MBR } idChild_area: array of Integer; { . , MBR , MBR } id_zero: Integer; { MBR ( MBR) } enlargement_mbr: TMBR; // MBR dx, dy, dspace: Double; // MBR x, y has_no_enlargement: Boolean; // begin if FNodeArr[node_id].isLeaf then // , begin Exit; end; SetLength(idChild_overlap, 1); SetLength(idChild_area, 1); dx := 0; dy := 0; dspace := 9999999; id_zero := 0; has_no_enlargement := False; min_overlap_enlargement := 999999; if FNodeArr[FNodeArr[node_id].Children[0]].isLeaf then // () begin { } for i := 0 to High(FNodeArr[node_id].FChildren) do begin id_child := FNodeArr[node_id].FChildren[i]; Overlap_enlargement := FNodeArr[id_child].Area(obj.mbr) - FNodeArr[id_child].Overlap(obj.mbr); if Overlap_enlargement <= min_overlap_enlargement then begin if Overlap_enlargement = min_overlap_enlargement then // begin SetLength(idChild_overlap, Length(idChild_overlap) + 1); idChild_overlap[ High(idChild_overlap)] := i; end else // begin min_overlap_enlargement := Overlap_enlargement; if Length(idChild_overlap) = 1 then // idChild_overlap[0] := i else begin SetLength(idChild_overlap, 1); // , 1 idChild_overlap[0] := i end; end; end; end; if Length(idChild_overlap) = 1 then // 1 begin node_id := FNodeArr[node_id].Children[idChild_overlap[0]]; chooseSubtree(obj, node_id); // Exit; end; end else // begin SetLength(idChild_overlap, Length(FNodeArr[node_id].FChildren)); for i := 0 to High(FNodeArr[node_id].FChildren) do // idChild_overlap, ( , idChild_overlap ) idChild_overlap[i] := i; end; { } for i := 0 to High(idChild_overlap) do begin id_child := FNodeArr[node_id].FChildren[idChild_overlap[i]]; enlargement_mbr.Left.X := Min(obj.mbr.Left.X, FNodeArr[id_child].mbr.Left.X); enlargement_mbr.Left.Y := Min(obj.mbr.Left.Y, FNodeArr[id_child].mbr.Left.Y); enlargement_mbr.Right.X := Max(obj.mbr.Right.X, FNodeArr[id_child].mbr.Right.X); enlargement_mbr.Right.Y := Max(obj.mbr.Right.Y, FNodeArr[id_child].mbr.Right.Y); area_enlargement := FNodeArr[id_child].Area(enlargement_mbr) - FNodeArr[id_child].Area; if area_enlargement <= dspace then begin if area_enlargement = dspace then // begin SetLength(idChild_area, Length(idChild_area) + 1); idChild_area[ High(idChild_area)] := i; end else // begin dspace := area_enlargement; if Length(idChild_area) = 1 then // idChild_area[0] := i else begin SetLength(idChild_area, 1); // , 1 idChild_area[0] := i end; end; end; end; if Length(idChild_area) = 1 then // , MBR begin node_id := FNodeArr[node_id].Children[idChild_area[0]]; chooseSubtree(obj, node_id); // end else // ( MBR ) MBR begin dspace := 999999; for i := 0 to High(idChild_area) do begin id_child := FNodeArr[node_id].Children[idChild_area[i]]; if FNodeArr[id_child].Area < dspace then begin id_zero := idChild_area[i]; dspace := FNodeArr[id_child].Area; end; end; node_id := FNodeArr[node_id].Children[id_zero]; chooseSubtree(obj, node_id); end; end; constructor TRtree.Create; begin inherited; SetLength(FNodeArr, 1); FNodeArr[0] := TRNode.Create; FRoot := 0; FNodeArr[FRoot].FisLeaf := True; end; destructor TRtree.Destroy; var i: Integer; begin for i := 0 to High(FNodeArr) do FreeAndNil(FNodeArr[i]); SetLength(FNodeArr, 0); inherited; end; procedure TRtree.findObjectsInArea(mbr: TMBR; node_id: Integer; var obj: TObjArr); var i: Integer; begin if isRoot(node_id) then SetLength(obj, 0); if not FNodeArr[node_id].isLeaf then begin for i := 0 to High(FNodeArr[node_id].FChildren) do begin if FNodeArr[FNodeArr[node_id].Children[i]].isIntersected(mbr) then findObjectsInArea(mbr, FNodeArr[node_id].Children[i], obj); end; end else begin for i := 0 to High(FNodeArr[node_id].FObjects) do begin if FNodeArr[node_id].isIntersected(mbr, FNodeArr[node_id].Objects[i].mbr) then begin SetLength(obj, Length(obj) + 1); obj[ High(obj)] := FNodeArr[node_id].Objects[i].idx; end; end; end; end; procedure TRtree.findObjectsInArea(mbr: TMBR; var obj: TObjArr); begin findObjectsInArea(mbr, FRoot, obj); end; procedure TRtree.insertObject(obj: TRObject); var node_id: Integer; begin node_id := FRoot; chooseSubtree(obj, node_id); if Length(FNodeArr[node_id].FObjects) < MAX_M then // begin FNodeArr[node_id].Objects[ High(FNodeArr[node_id].FObjects) + 1] := obj; updateMBR(node_id); end else // begin splitNodeRStar(node_id, obj); // end; end; function TRtree.isRoot(node_id: Integer): Boolean; begin if node_id = FRoot then Result := True else Result := False; end; function TRtree.newNode: Integer; begin SetLength(FNodeArr, Length(FNodeArr) + 1); FNodeArr[ High(FNodeArr)] := TRNode.Create; Result := High(FNodeArr); end; procedure TRtree.QuickSort(var List: array of TRObject; iLo, iHi: Integer; axe: TAxis; bound: TBound); var Lo: Integer; Hi: Integer; T: TRObject; Mid: Double; begin Lo := iLo; Hi := iHi; case bound of Left: case axe of X: Mid := List[(Lo + Hi) div 2].mbr.Left.X; Y: Mid := List[(Lo + Hi) div 2].mbr.Left.Y; end; Right: case axe of X: Mid := List[(Lo + Hi) div 2].mbr.Right.X; Y: Mid := List[(Lo + Hi) div 2].mbr.Right.Y; end; end; repeat case bound of Left: case axe of X: begin while List[Lo].mbr.Left.X < Mid do Inc(Lo); while List[Hi].mbr.Left.X > Mid do Dec(Hi); end; Y: begin while List[Lo].mbr.Left.Y < Mid do Inc(Lo); while List[Hi].mbr.Left.Y > Mid do Dec(Hi); end; end; Right: case axe of X: begin while List[Lo].mbr.Right.X < Mid do Inc(Lo); while List[Hi].mbr.Right.X > Mid do Dec(Hi); end; Y: begin while List[Lo].mbr.Right.Y < Mid do Inc(Lo); while List[Hi].mbr.Right.Y > Mid do Dec(Hi); end; end; end; if Lo <= Hi then begin T := List[Lo]; List[Lo] := List[Hi]; List[Hi] := T; Inc(Lo); Dec(Hi); end; until Lo > Hi; if Hi > iLo then QuickSort(List, iLo, Hi, axe, bound); if Lo < iHi then QuickSort(List, Lo, iHi, axe, bound); end; procedure TRtree.QuickSort(var List: array of Integer; iLo, iHi: Integer; axe: TAxis; bound: TBound); var Lo: Integer; Hi: Integer; T: Integer; Mid: Double; begin Lo := iLo; Hi := iHi; case bound of Left: case axe of X: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Left.X; Y: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Left.Y; end; Right: case axe of X: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Right.X; Y: Mid := FNodeArr[List[(Lo + Hi) div 2]].mbr.Right.Y; end; end; repeat case bound of Left: case axe of X: begin while FNodeArr[List[Lo]].mbr.Left.X < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Left.X > Mid do Dec(Hi); end; Y: begin while FNodeArr[List[Lo]].mbr.Left.Y < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Left.Y > Mid do Dec(Hi); end; end; Right: case axe of X: begin while FNodeArr[List[Lo]].mbr.Right.X < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Right.X > Mid do Dec(Hi); end; Y: begin while FNodeArr[List[Lo]].mbr.Right.Y < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Right.Y > Mid do Dec(Hi); end; end; end; if Lo <= Hi then begin T := List[Lo]; List[Lo] := List[Hi]; List[Hi] := T; Inc(Lo); Dec(Hi); end; until Lo > Hi; if Hi > iLo then QuickSort(List, iLo, Hi, axe, bound); if Lo < iHi then QuickSort(List, Lo, iHi, axe, bound); end; procedure TRtree.splitNodeRStar(splited_Node_Id, inserted_Node_Id: Integer); var axe: TAxis; parent_id, new_child_id: Integer; node_1, node_2, node_1_min, node_2_min: TRNode; i, j, k: Integer; arr_node: array of Integer; area_overlap_min, area_overlap, // area_min, Area: Double; // begin if FNodeArr[splited_Node_Id].isLeaf then Exit; if isRoot(splited_Node_Id) then begin parent_id := newNode; // id FNodeArr[FRoot].Parent := parent_id; // id , FNodeArr[parent_id].Children[0] := FRoot; // id FNodeArr[parent_id].Level := FNodeArr[FNodeArr[parent_id].Children[0]].Level + 1; // 1 FRoot := parent_id; // id id FHeight := FHeight + 1; // end else begin parent_id := FNodeArr[splited_Node_Id].Parent; end; SetLength(arr_node, MAX_M + 1); for i := 0 to High(arr_node) - 1 do arr_node[i] := FNodeArr[splited_Node_Id].Children[i]; arr_node[ High(arr_node)] := inserted_Node_Id; node_1_min := TRNode.Create; node_2_min := TRNode.Create; node_1 := TRNode.Create; node_2 := TRNode.Create; axe := chooseSplitAxis(splited_Node_Id, inserted_Node_Id); area_overlap_min := 9999999; area_min := 9999999; for i := 0 to 1 do begin QuickSort(arr_node, 0, High(arr_node), axe, TBound(i)); for k := MIN_M - 1 to MAX_M - MIN_M do begin node_1.clearChildren; node_2.clearChildren; j := 0; while j <= k do begin node_1.Children[j] := arr_node[j]; j := j + 1; end; for j := k to High(arr_node) - 1 do begin node_2.Children[j - k] := arr_node[j + 1]; end; updateMBR(node_1); updateMBR(node_2); area_overlap := node_1.Overlap(node_2.mbr); if area_overlap < area_overlap_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_overlap_min := area_overlap; end else begin if area_overlap = area_overlap_min then // begin Area := node_1.Area + node_2.Area; // if Area < area_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_min := Area; end; end; end; end; end; node_1_min.Level := FNodeArr[splited_Node_Id].Level; node_2_min.Level := FNodeArr[splited_Node_Id].Level; FNodeArr[splited_Node_Id].copy(node_1_min); // () FNodeArr[splited_Node_Id].Parent := parent_id; new_child_id := newNode; // FNodeArr[new_child_id].copy(node_2_min); // FNodeArr[new_child_id].Parent := parent_id; // id parent FreeAndNil(node_1); FreeAndNil(node_2); FreeAndNil(node_1_min); FreeAndNil(node_2_min); for i := 0 to High(FNodeArr[new_child_id].FChildren) do // Parent id begin FNodeArr[FNodeArr[new_child_id].Children[i]].Parent := new_child_id end; if Length(FNodeArr[parent_id].FChildren) < MAX_M then // begin FNodeArr[parent_id].Children[ High(FNodeArr[parent_id].FChildren) + 1] := new_child_id; // id updateMBR(parent_id); end else // begin splitNodeRStar(parent_id, new_child_id); // end; end; procedure TRtree.splitNodeRStar(node_id: Integer; obj: TRObject); var axe: TAxis; parent_id, new_child_id: Integer; node_1, node_2, node_1_min, node_2_min: TRNode; i, j, k: Integer; arr_obj: array of TRObject; area_overlap_min, area_overlap, // area_min, Area: Double; // begin if not FNodeArr[node_id].isLeaf then Exit; if isRoot(node_id) then begin parent_id := newNode; // id FNodeArr[FRoot].Parent := parent_id; // id , FNodeArr[parent_id].Children[0] := FRoot; // id FNodeArr[parent_id].Level := FNodeArr[FNodeArr[parent_id].Children[0]].Level + 1; // 1 FRoot := parent_id; // id id FHeight := FHeight + 1; // end else begin parent_id := FNodeArr[node_id].Parent; end; SetLength(arr_obj, MAX_M + 1); for i := 0 to High(arr_obj) - 1 do arr_obj[i] := FNodeArr[node_id].Objects[i]; arr_obj[ High(arr_obj)] := obj; node_1_min := TRNode.Create; node_2_min := TRNode.Create; node_1 := TRNode.Create; node_2 := TRNode.Create; axe := chooseSplitAxis(obj, node_id); area_overlap_min := 9999999; area_min := 9999999; for i := 0 to 1 do begin QuickSort(arr_obj, 0, High(arr_obj), axe, TBound(i)); for k := MIN_M - 1 to MAX_M - MIN_M do begin node_1.clearObjects; node_2.clearObjects; j := 0; while j <= k do begin node_1.Objects[j] := arr_obj[j]; j := j + 1; end; for j := k to High(arr_obj) - 1 do begin node_2.Objects[j - k] := arr_obj[j + 1]; end; updateMBR(node_1); updateMBR(node_2); area_overlap := node_1.Overlap(node_2.mbr); if area_overlap < area_overlap_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_overlap_min := area_overlap; end else begin if area_overlap = area_overlap_min then // begin Area := node_1.Area + node_2.Area; // if Area < area_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_min := Area; end; end; end; end; end; node_1_min.Level := 0; node_2_min.Level := 0; FNodeArr[node_id].copy(node_1_min); // () FNodeArr[node_id].Parent := parent_id; updateMBR(node_id); new_child_id := newNode; // FNodeArr[new_child_id].copy(node_2_min); // FNodeArr[new_child_id].Parent := parent_id; // id parent updateMBR(new_child_id); FreeAndNil(node_1); FreeAndNil(node_2); FreeAndNil(node_1_min); FreeAndNil(node_2_min); if Length(FNodeArr[parent_id].FChildren) < MAX_M then // begin FNodeArr[parent_id].Children[ High(FNodeArr[parent_id].FChildren) + 1] := new_child_id; // id updateMBR(parent_id); end else // begin splitNodeRStar(parent_id, new_child_id); // end; end; procedure TRtree.updateMBR(node: TRNode); var i, idx: Integer; changed: Boolean; begin changed := False; node.fmbr.Left.X := 9999; node.fmbr.Left.Y := 9999; node.fmbr.Right.X := 0; node.fmbr.Right.Y := 0; if node.isLeaf then begin for i := 0 to High(node.FObjects) do begin if node.FObjects[i].mbr.Left.X < node.mbr.Left.X then begin node.fmbr.Left.X := node.FObjects[i].mbr.Left.X; changed := True; end; if node.FObjects[i].mbr.Left.Y < node.mbr.Left.Y then begin node.fmbr.Left.Y := node.FObjects[i].mbr.Left.Y; changed := True; end; if node.FObjects[i].mbr.Right.X > node.mbr.Right.X then begin node.fmbr.Right.X := node.FObjects[i].mbr.Right.X; changed := True; end; if node.FObjects[i].mbr.Right.Y > node.mbr.Right.Y then begin node.fmbr.Right.Y := node.FObjects[i].mbr.Right.Y; changed := True; end; end; end else begin for i := 0 to High(node.FChildren) do begin idx := node.FChildren[i]; if FNodeArr[idx].mbr.Left.X < node.mbr.Left.X then begin node.fmbr.Left.X := FNodeArr[idx].mbr.Left.X; changed := True; end; if FNodeArr[idx].mbr.Left.Y < node.mbr.Left.Y then begin node.fmbr.Left.Y := FNodeArr[idx].mbr.Left.Y; changed := True; end; if FNodeArr[idx].mbr.Right.X > node.mbr.Right.X then begin node.fmbr.Right.X := FNodeArr[idx].mbr.Right.X; changed := True; end; if FNodeArr[idx].mbr.Right.Y > node.mbr.Right.Y then begin node.fmbr.Right.Y := FNodeArr[idx].mbr.Right.Y; changed := True; end; end; end; if changed then begin if node.Parent >= 0 then updateMBR(node.Parent); end; end; procedure TRtree.updateMBR(node_id: Integer); var i, idx: Integer; changed: Boolean; begin changed := False; FNodeArr[node_id].fmbr.Left.X := 9999; FNodeArr[node_id].fmbr.Left.Y := 9999; FNodeArr[node_id].fmbr.Right.X := 0; FNodeArr[node_id].fmbr.Right.Y := 0; if FNodeArr[node_id].isLeaf then begin for i := 0 to High(FNodeArr[node_id].FObjects) do begin if FNodeArr[node_id].FObjects[i].mbr.Left.X < FNodeArr[node_id].mbr.Left.X then begin FNodeArr[node_id].fmbr.Left.X := FNodeArr[node_id].FObjects[i].mbr.Left.X; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Left.Y < FNodeArr[node_id].mbr.Left.Y then begin FNodeArr[node_id].fmbr.Left.Y := FNodeArr[node_id].FObjects[i].mbr.Left.Y; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Right.X > FNodeArr[node_id].mbr.Right.X then begin FNodeArr[node_id].fmbr.Right.X := FNodeArr[node_id].FObjects[i].mbr.Right.X; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Right.Y > FNodeArr[node_id].mbr.Right.Y then begin FNodeArr[node_id].fmbr.Right.Y := FNodeArr[node_id].FObjects[i].mbr.Right.Y; changed := True; end; end; end else begin for i := 0 to High(FNodeArr[node_id].FChildren) do begin idx := FNodeArr[node_id].FChildren[i]; if FNodeArr[idx].mbr.Left.X < FNodeArr[node_id].mbr.Left.X then begin FNodeArr[node_id].fmbr.Left.X := FNodeArr[idx].mbr.Left.X; changed := True; end; if FNodeArr[idx].mbr.Left.Y < FNodeArr[node_id].mbr.Left.Y then begin FNodeArr[node_id].fmbr.Left.Y := FNodeArr[idx].mbr.Left.Y; changed := True; end; if FNodeArr[idx].mbr.Right.X > FNodeArr[node_id].mbr.Right.X then begin FNodeArr[node_id].fmbr.Right.X := FNodeArr[idx].mbr.Right.X; changed := True; end; if FNodeArr[idx].mbr.Right.Y > FNodeArr[node_id].mbr.Right.Y then begin FNodeArr[node_id].fmbr.Right.Y := FNodeArr[idx].mbr.Right.Y; changed := True; end; end; end; if changed then begin if FNodeArr[node_id].Parent >= 0 then updateMBR(FNodeArr[node_id].Parent); end; end; end.
実装後は、ベクターマップオブジェクトをレイヤーに分割し、これらのレイヤーを表示される最大スケールに設定し、各レイヤーのR *ツリーを構築するだけでした。
結果はビデオで見ることができます: