コードを含むWolfram Mathematicaファイルを含むアーカイブは、 こちらからダウンロードできます 。
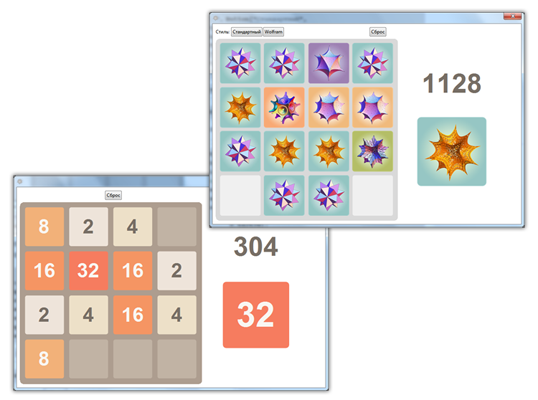
過去数週間でオンラインになった場合、ガブリエル・チルリが開発した2048というゲームに出会うことはほとんどなかったでしょう。 同様のゲームに基づいて、 1024! Veewo Studioから、Asher WollmerからTHREESまで、このゲームには長い間あなたを引きずる単純なメカニズムがあります-2で書かれた度数を持つフィールド上のチップを動かし、さらに高い度を得るためにそれらをペアで接続します。 このゲームの主な目標は2048チップを手に入れることですが、このゲームがどれほど面白くてエキサイティングなのかを説明するのは難しいので、自分でプレイすることをお勧めします。
この単純なゲーム(およびすべての数学ゲーム!)を評価するために、 Wolfram言語のフルパワーを実証し、それを使用して2048の独自バージョンを開発することにしました。始めましょう!
競技場の基本構造は、空の要素(長さゼロの行)で満たされた4x4マトリックスです。
[1]で:=
アウト[2] =
新しいゲームを開始した後、値2または4の2つのチップをフィールドにランダムに配置します。チップ2を優先するため、より頻繁にフィールドに表示されます。
[3]で:=

[4]で:=

アウト[4] =
競技場をもう少し美しくする時が来ました。 CSSスタイル(CSS-Cascading Style Sheets、Cascading Style Sheets)をインポートすることで、元のゲームのスタイルを完全に繰り返すことができます。 ご覧のとおり、CSSでは、すべてのチップの背景とテキストの色を見つけることができました。
[5]で:=

アウト[8] =

これで、各チップ番号とそれに対応する色を含むリストができました! 次に、色を見つけてHEX(CSSで使用される色の16進表記)からRGB(赤、緑、青の組み合わせに基づくカラーモデル)に変換する関数を作成することで処理できます。 また、競技場の残りの部分と、念のためにデフォルトでいくつかの色の色を定義します。
[9]で:=

[10]で:=

[13]で:=

次に、色情報を使用して、チップを描画する関数を記述します。 数字の桁数が増えると、フォントサイズが小さくなるように注意する必要があります。
[15]で:=

[16]で:=

[17]で:=
後で簡単に変更できるようにdrawTile関数を定義しました...
[18]で:=
アウト[18] =
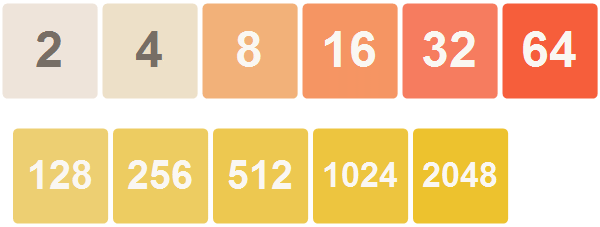
このスタイルを元の競技場に適用するには、マトリックス内の競技場の各要素を見て、対応するチップを正しい場所に配置するだけです。
[19]で:=

[20]で:=

アウト[20] =

きれいに見えます! 次に、ゲームを制御する方法を学ぶ必要があります。
キーの1つを押すと、すべてのチップがボードに沿って指示された方向に可能な限り移動し、同じチップが結合されます。 NotebookEventActionsオプションを使用してキーストロークを記録し、適切に応答できます。 コントロールが無駄なキーで実行されることを確認します。他のものを選択できます:
[21]で:=
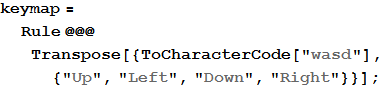
[22]で:=

次に、チップが左に移動したとき、たとえば何が起こるかを考えてみましょう。 まず、同じチップの結合を実装する必要があります。 水平方向の一致は垂直方向の一致を結合しないため、各行を個別に考慮する必要があります。 空のセルが間にある可能性のある2つの同じ数のシーケンスを見つけて、合計に置き換えたいと思います。 Wolfram言語の力がここで助けになります。そして、これを簡単に達成するために、指定されたワイルドカード表現とのマッチングを使用できます。
[23]で:=
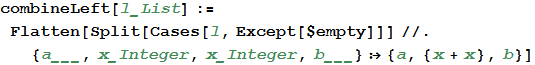
同じチップを追加した後、行を埋めるために空の要素を右側にいくつか追加するだけです。 この手順は、競技場のすべての行に対して繰り返されます。
[24]で:=
右側へのシフトも同じ方法で実行されますが、わずかな変更が1つあります。右側の同じチップの組み合わせを左側の組み合わせに結合したいのです。 例として、文字列{$ empty、2、2、2}を考えてください。 composeLeft関数を使用して左矢印を押すと、文字列{$ empty、$ empty、4、2}を取得しますが、実際には2つの正しいペアを最初に結合する必要があります。 ラインフリップ、左セルシフト、およびリバースフリップは、問題を簡単に解決します。
[25]で:=
[26]で:=
これら2つの関数が用意できたので、上下シフトを実装するのは非常に簡単です! 上へのシフトは、移調された競技場での左シフトと同じで、その後に逆の移調が続きます。 左右へのシフトも同じ関係で関連付けられます。
[27]で:=

キーが押された場合、フィールドの状態が変更された場合、つまり一部のチップが移動またはマージされた場合にのみ、フィールドに新しいチップを追加する必要があります。 これを行うには、競技場の以前の状態を監視する必要があります。
次に、ゲーム中にポイントをカウントする方法を学びます。 2つのチップが結合されるたびに、 Sow関数で合計を収集し、可能なすべての組み合わせが完了したら、すべての合計でReap関数を使用します。 また、現在受け取っている最大のチップの値も表示します。
[29]で:=

最後に、勝ち負けテストを追加しましょう。 フィールド上の最大のチップの値が2048以上の場合、ゲームに勝ったと見なされます。 ボードがいっぱいになり、移動が不可能になった場合、負けとなりました。 この場合も、テンプレート式の言語を使用して、チップの組み合わせがボード上に残っているかどうかを判断できます。
[30]で:=

[31]で:=
ダイナミック機能を使用すると、行われた変更に応じて、表示されるプレイフィールドを完全に維持できます。 さらに、これらすべてをDynamicModule関数で囲み、 初期化を使用してキーストロークの処理とプレイフィールドをカスタマイズできます。 DynamicDialogをCreateDialog内に配置することにより、別のウィンドウでゲームを開くことができます。
最後に、ゲームは完全に準備ができています。
[32]で:=


今ではすべてがとてもきれいに見えますが、Wolfram Researchではもっと何かが大好きです... Spikeyなど-さまざまなバージョンのMathematicaおよびWolfram | Alphaシステムのロゴ。 チップの色と形状を少し変えてみましょう。
[33]で:=
[34]で:=
アウト[34] =

[35]で:=

[36]で:=
[37]で:=
[39]で:=
これで、ボタンを使用して2つのスタイルを切り替えることができます。
[40]で:=

アウト[40] =
[41]で:=

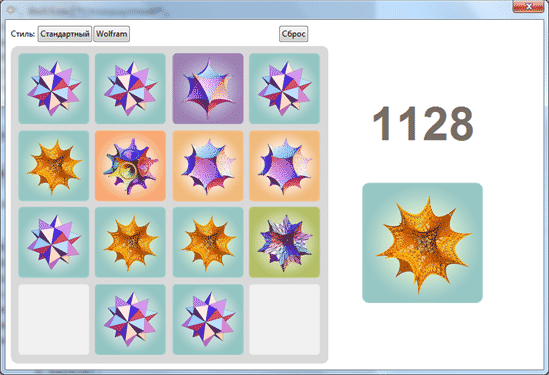
あなたのゲームで頑張ってください!