学校からは、平面上の点電荷の存在下で、無限導電面上の電荷の分布の問題の解決策を覚えています。 点電荷が空間のどこかにある場合に、導電性球体上の電荷分布の問題がどのように解析的に解決されるかを覚えているのは一部の人だけです。 しかし、私は、誰もクラインのボトルの電荷の分布の同様の問題を解決することができないと確信しています。 このようなシステムに外部静電界と他の導体を追加すると、分析ソリューションを夢見ることさえ愚かでしょう。
静電気の一般的な問題を次のように定式化します。
与えられた：
-導体の空間内の形状と位置
-導体の充電
-外部電界（導体の位置に関係なく、導体がない場合の電界）
導体の表面全体の電荷分布と空間全体の電界のスカラーポテンシャルを見つける必要があります 。
3つのデカルト座標の関数としてのポテンシャルは、空間全体でポアソン方程式を満たさなければなりません。
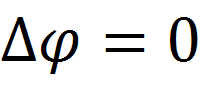
一意性定理から、この方程式と境界条件を満足する関数を見つけた場合、つまり ソリューション、このソリューションが唯一のものになります。
不要な複雑さを回避するために、導電性表面の位置と電荷に依存しない外部場の存在下で、導電性表面上の電荷の分布の問題の解決策を検討します。
有限要素法により数値的に問題の解決策を模索します。
私はすぐに、私の方法の収束の問題を理論的には考えないことを警告しますが、実際のいくつかの事実に自分自身を制限し、この方法の収束の仮説を支持して証言します。
表面をパラメトリックに定義します。
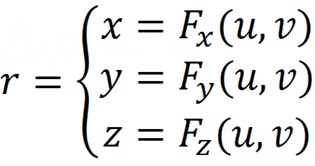
uとv-パーティションの数を選択し、表面をuとvのネットワークでカバーします-ライン。 結果のグリッドのノードに電荷を配置します。その値を見つける必要があります。
また、ノードのすぐ近くにあるNu * Nvポイントを選択します。 これらの点での電界の電位が同じであるという条件に基づいた解決策を探します。 ポテンシャル自体は、ポイントチャージによって作成されたポテンシャルの重ね合わせとして計算されます。
行列を作成します。
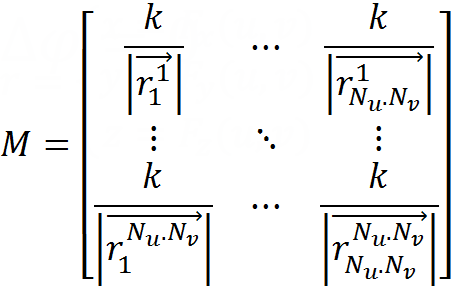-解決する線形システムの行列のスケッチ。 下のインデックスは電荷の位置を示し、上のインデックスは電位の考慮点を示します。 これらの距離は、表面のパラメーター化から求められます。
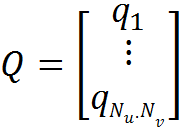-未知数の列行列-料金の値。
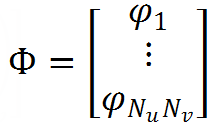- ポテンシャルの考慮点での外部場のポテンシャルの列行列。
次に、システムΦ+ MQ = Aを取得します。ここで、 Aは、未知の表面電位で構成される一定の列行列です。
このポテンシャルをシステムから除外するには、まず行列Φを等式の右側に転送し、次にシステムの最初の方程式をNu * Nv-1から減算し、最後の方程式を正規化条件に置き換えます（表面上のすべての電荷の合計は総電荷に等しくなります）。
次に、システム行列を使用して最終的な線形システムを取得します。
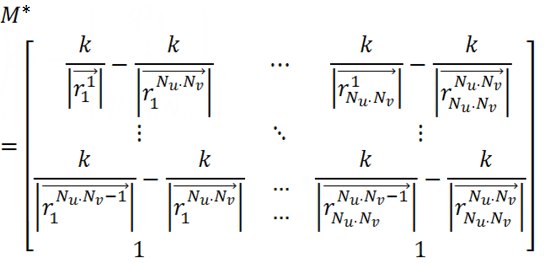
そして無料メンバーの列：
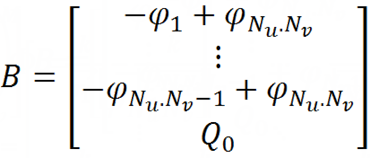
これらの写真を過度に大きなフォントで終了するには、すべての作業の結果を定義する最後の式を与えます-表面上の電荷の表面の区分的定数関数（同じインデックスを持つ近似領域に属するuとvの場合、関数は左側の値を取ります式）：
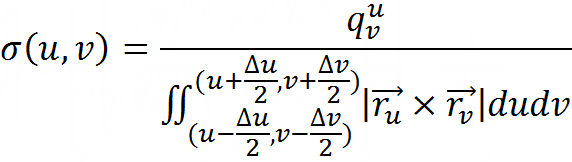
システムを解決し、Mathematicaシステムで結果を処理します。
静電気の一般的な問題に対する特定の解決策nb
次にメソッドを見てみましょう。 簡単な方法でパラメーター化された正方形のプレートから始めます。 次に、パラメーターuおよびvはプレート点のデカルト座標であり、面積要素は上記の積分の下にあり、1に等しくなります。
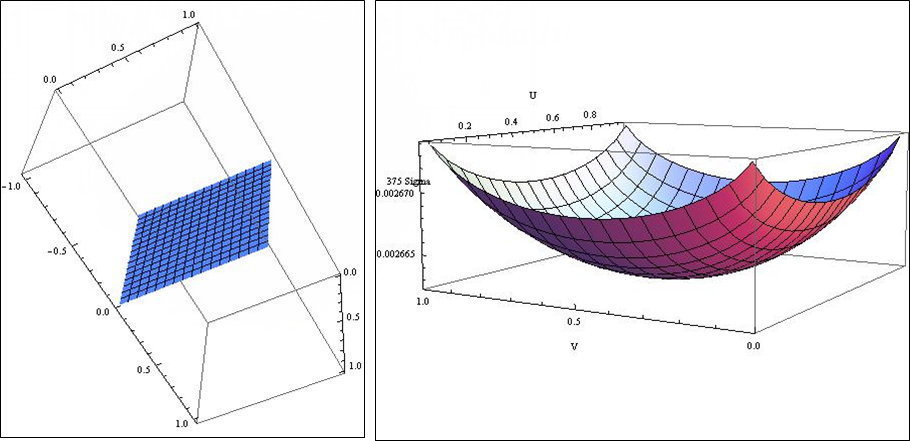
論理的で期待されるソリューションを得ました。
球の解決策は平面でなければなりませんが、完全に悪いことがあります。
しかし、すべてがそれほど悪いわけではありません。 ノードの数が増えると、この図は縮小します（ただし、自動生成された数学グラフでは、これは表示されません）。
解を求める表面は閉じている必要があります。閉じていないと、エッジに特異性が生じる可能性があります。精度が上がると、エッジの電荷密度は無限になります。
また、メソッドの動作をテストするために、2つの方法で半円（「ビーズ」）の電荷分布の問題を解決することにしました。
方法1.同じ電荷をビーズに加えます。 無慣性料金。 それらを手放します。 小さなステップで、彼らは安定した位置を取ります。 電荷の角度座標に関するZeidelタイプの視覚的方法：
方法2。上記のシステムは、3次元空間の半円柱に対応し、この方法で問題を解決します。
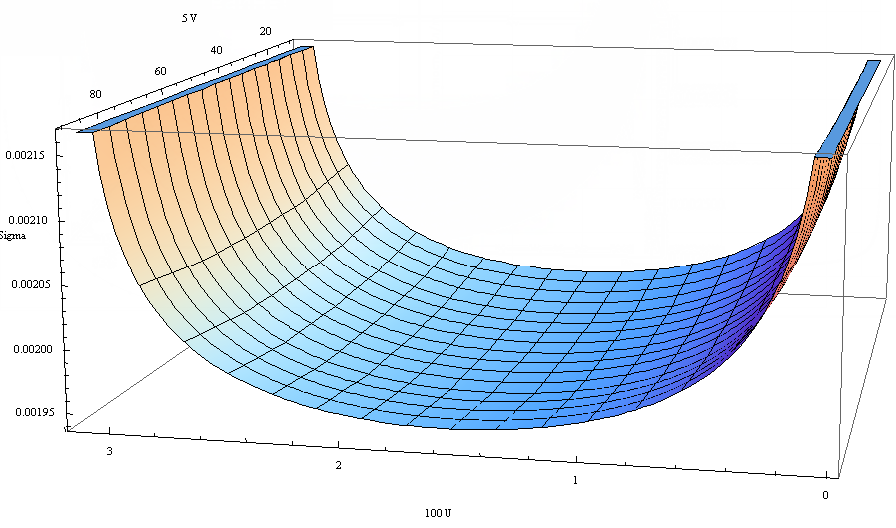
外側では、ソリューションは非常に似ています。
静電気の一般的な問題を解決する上記の方法についてのあなたの意見を聞くのは興味深いです。