ちなみに、ShADに行くには早すぎるが、約束を示す知人や子供がいる場合は、Yandexの参加で今年経済高等学校で開かれるコンピューターサイエンス学部について教えてください。 多くの点で、データ分析学部から成長しますが、私たちは学生と卒業生を受け入れます。 したがって、応募者の方は、4月27日にこの学部のプレゼンテーションに出席してください。ヤロスラフ・クズミノフ経済学部長とヤンデックスの共同設立者であるアルカディ・ヴォロシュが彼に関する詳細を説明します。 みんなを招待します。
ストーリー：1つはGooglerについて、もう1つはYandexの従業員について
ShADの作成以来、コンピューターサイエンスの分野の260人の専門家がこれを完了しました。 学校の2人の卒業生に、その研修で得られたものについて話し、それを行うことを決めた人にアドバイスをするように依頼しました。
Googleのミュンヘンオフィスの開発者であるAndrey Petrov。
私が学生だったとき、プログラミングの方法をすでに知っているという幻想があり、コンピューターサイエンスは簡単です。 確かに、私は動的なコンテンツでウェブサイトを作成し、ゲームを書いて、オリンピックで賞を受け取り、問題なく大学で試験に合格したためです。 しかし、それは趣味であり、私はアマチュアでした。 プロの道を歩むために、私はヤンデックスの学校に行きました。
そこですぐに、開発はコードを書くのではなく、スタイルに従って、プラクティスを使用し、ドキュメントをサポートし、ソフトウェアをテストすることを学びました。 そこで、初めて、機械学習の非常に関連性の高い科学を知ることができました。厳密な数学的基礎について学ぶ方法と、実際のデータで多くの実験を行い、同僚と品質の割合を競う方法の両方です。 そこで私は視野を広げ、一度に対処できないという事実だけを後悔している業界に精通しました。画像認識、コンピューター言語、インターネット検索、現代のグラフアルゴリズムです。 最後に、そこで素晴らしい人々に出会い、その多くは後に同僚や友人になりました。
あなたが行動するかどうかを検討していて、私と同じ幻想を抱いているなら、今あなたは何をすべきか知っています。 幻想がなくても、それは非常に有用で興味深いものです。 データ分析の科学とIT業界の両方に専門家が必要です。 彼らに参加するには、長い道のりを歩かなければなりません。SHADへの入場は、この方向への重大な一歩です。
ShADを卒業したAlexey Umnov。 Yandexの検索形態グループの開発者、VMKモスクワ州立大学の大学院生。
SHADでは、多くの有用な理論的および実践的知識を受け取りました。 Yandex内のプロジェクトと他のエリアの両方で私にとって有用でした。 たとえば、科学活動では、機械学習コースで得た知識とさまざまなプログラミングスキルを非常に積極的に使用しています。 また、SHADで提供されるすべての資料は非常に現代的であり、コンピューターサイエンスのような急速に発展している分野にとって非常に重要であることに注意してください。
私は将来の学生にかなり馴染みのない形式のトレーニングではなくかなり大きな負荷に備えるようアドバイスします：コースの良い成績を得るには、学期を通して宿題をとる必要があり、最終的なコントロールまたは試験はこれには十分ではありません。
導入タスクの分析
今回、データ分析学部の筆記試験のすべてのタスクを公に分析することを初めて決定しました。 アンケートのタスクを正常に完了した人のみが許可されます。 昨年、617人のうち284人が招待を受け、132人が合格し、インタビューに合格しました。
タスク1
シーケンス
再帰的に定義されます。
シーケンス内の共通用語の式を見つけます。
解決策
表記を紹介します
それから 
また
。 わかった 
ここから
タスク2
集合A = {1,2、...、n}を与えます。 すべてのサブセットの中から 、サブセットA 1 、...、A kのkを等しく選択する可能性があります。 A 1∩A 2∩...∩A k = thatとなる確率を求めます。
解決策
要素i∈Aを考えます。 明らかに、 iを含むAと iを含まないAのサブセットの数は等しくなります。 したがって、 iがA jに存在する確率は1/2です。 これらの確率は、異なるjに対して独立しています。 iが A 1∩A 2∩...∩A kに含まれる確率は1/2 kです。 したがって、 iが A 1∩A 2∩...∩A kに含まれない確率は 1-1
タスク3
ゼロと1の長さnの配列が与えられます。 その中に、ユニット数がゼロの数に等しい最大長のサブ配列を見つけます。 制限：時間内のO（ n ）および追加メモリ内のO（ n ）。
解決策
元の配列を[・]で示します。 長さnの 4つの配列をさらに開始します。b [・]、 c [・]、 d [・]およびe [・]。 増加するインデックスを調べて、ルールに従って配列b [・]を埋めます。b [0] = 2・a [0]-1、 b [ i ] = b [ i -1] + 2 a [ i ]-1 for i > 0.つまり、配列a [・]でゼロが-1に置き換えられると、 a [0]からa [ i ]への合計は配列b [・]になります。 配列をc [・]およびd [・]マイナス1で埋めます。 次に、配列bの数字の昇順で進みます[・]。 b [ i ] = kの場合、 d [ k ] = i 、 c [ k ] = -1の場合、 c [ k ] = iを割り当てます 。
さらに、配列b [・]全体を調べたとき、規則e [ i ] = d [ i ] -c [ i ]に従って配列e [・]を埋めます。 配列a [・]にa [ m ]からa [ l ]への部分配列があり、1と0の数が等しい場合、 b [ m ] = b [ l ] = kであることに注意してください。 そして、 c [ k ]はb [ i ] = kであるような最小数iであり、 d [ k ]は最大です。 したがって、 e [ k ]はmとlの間の最大距離です。ここで、 b [ m ] = b [ l ] = kです。 配列e [・]の最大値を見つけます。 （明らかに、これはO（ n ）操作で行うことができます。） e [ j ]と等しくなるようにします。 目的のサブアレイは、 a [ c [ j ]]からa [ d [ j ]]までのサブアレイです。
タスク4
させて
どのm∈[0、10] I m ≠0？
解決策
式を繰り返し使用します。
この式を使用すると、次が得られます。
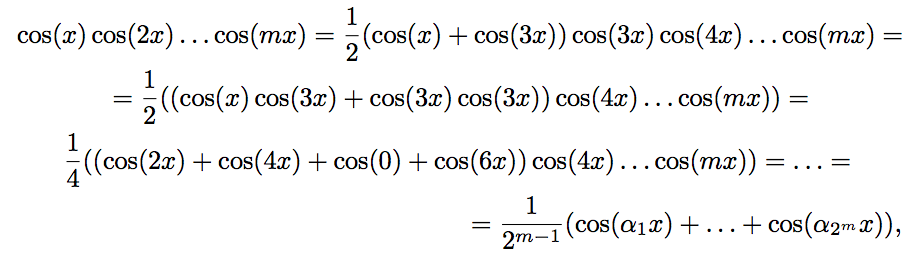ここで、a i = 1±2±3 ...±m∈Z すべての数値a iのパリティが同じであることを確認するのは簡単です。 さらに、 m = 4kおよびm = 4k + 3の場合、すべてのa iは偶数です。 a i ≠0の場合、 
したがって、 m = 4k + 1およびm = 4k + 2の場合、 I m = 0です。 m = 4kまたは4k + 3の場合、数字i 、2、...、mの間に符号「+」と「-」を挿入してゼロを取得できるため、 a iにはゼロが必要です。 確かに
（1 + 2-3）+（4-5-6 + 7）+ ... +（4k-（4k + 1）-（4k + 2）+（4k + 3））= 0 。
したがって、 m = 4kおよび4k + 3 、 I m = 0です。 回答： m = 0.3.4.7.8で。
タスク5
ループのない無向グラフGが与えられます。 すべてのピークに番号を付けましょう。 有限数の頂点n （1からnまでの番号が付けられている）を持つグラフGの隣接行列は、サイズijの正方行列Aで 、ここでa ijの値はグラフのi番目の頂点からj番目の頂点までのエッジの数に等しくなります。
行列Aが負の固有値を持つことを証明します。
解決策
問題の記述が正しくありません。 グラフにエッジがない場合、マトリックスはゼロになり、すべての固有値はゼロに等しくなります。 エッジがある場合、 Aは非負の要素と対角要素にゼロを持つ対称行列です。 そのような行列が非負の固有値を持つことを証明しましょう。
対称行列が実際に対角化可能であることは周知の事実です。 （すべての固有値は実数です。） Aのすべての固有値が負でないと仮定します。 基底{e 1 、...、e n }に行列Aがある2次形式qを考えます。 この二次形式は、すべての固有値が非負であるため、非負定値です。 それは
一方、 a ij ≠0とします。 それからq（e i -e j ）= a ii -2a ij + a jj = -2a ij <0。これはqの非負定値と矛盾します。 したがって、最初の仮定は間違っており、 Aは負の固有値を持ちます。
タスク6
無限の2次元配列を考えます
自然数で構成され、各数は正確に8回発生します。 解決策
と仮定する
。 いくつかのk∈Nを選択し、平面y = k / xの曲線を考えます。 i、j∈Nで、点（i、j）が曲線y = k / xの下にある場合、a ij≤ij≤i・k / i = kです。 したがって、曲線y = k / xの下の整数点の数は8k以下でなければなりません。 一方、この曲線の下にある整数点の数は、 
kが十分に大きい場合、この数は8kより大きくなります。 したがって、矛盾が生じます。 したがって、 a mn > mnのようなペア（m、n）があります。
タスク7
ゼロと1の行列が与えられ、行列の各行に対して次のことが当てはまります。行に1がある場合、それらはすべて行（複雑な1のグループ）になります。 そのような行列の行列式は、±1または0になり得ることを証明します。
解決策
行を再配置することにより、最初の（左の）ユニットの位置が上から下に減少しないようにすることができます。 この場合、行列式は変化しないか、符号を変更します。 最初のユニットの位置が2つのラインで一致する場合、ユニットの数が多いユニットからユニットの数が少ないユニットを差し引きます。 行列式は変わりません。 このような操作により、最初のユニットの位置が厳密に上から下に増加することを保証できます。 この場合、行列は縮退するか、対角線上に単位がある上三角になることがわかります。 つまり、行列式は0または1のいずれかになります。行列式は操作中に変更されなかったか、符号が変更されたため、初期行列式は±1または0でした。
学校についてのもう少しの言葉
ロシアの有名な学者がShADで教えています。 たとえば、データ分析コースは、 ラトガース大学の教授であるイリヤ・ムニクによって開発および指導されました。 かつて彼はアルカディ・ヴォロシュの科学顧問を務めていました。 大量のデータを扱うことを想像することなく不可能な機械学習の理論は、ロンドン大学の教授であり、データ分析の国立学校の創設者の1人であるAlexey Chervonenkisによって教えられています。 コンピューターサイエンス部門のプログラムもイリヤセガロビッチによって開発されました。 ShADは、応用問題に学術的知識を応用できる世代のプログラマーを育成するために作成されました。 したがって、私たちは科学者だけでなく、Yandexの従業員にも教えられています。
昨年、入学願書を617件受け取り、筆記試験に284人が招待されました。 しかし、これは入学者にとって最後のテストではありません。 試験の結果に基づいて、面接に招待します。 合格して面接に合格した132人のうち、97人が初年度に登録されました。
多くの人が覚えているように、SHADは2007年に登場しました。 現在、エカテリンブルク、キエフ、ミンスク、ノボシビルスクに支社があります。 サンクトペテルブルクでは、 コンピューターサイエンスセンターに ShAD支店が開設されました。
トレーニングコースは2年間続きます。 プログラムは、理論（「離散分析」、「組み合わせ論」、「確率」、「複雑性理論」）、実践（「C ++プログラミングのトレーニング」、「Java」、「並列および分散コンピューティング」）の3種類のコースに分かれています。および混合（「アルゴリズムとデータ構造」、「機械学習」、「コンピューター言語学」など）。 通信部門で勉強し、教師と電子メールでやり取りし、ビデオ講義を使用することができます。