UPD:よりわかりやすくするために、テキストにいくつかの変更が加えられました。 セマンティックコンポーネントは同じままです。
エントリー
おそらくこのシステムにはアプリケーションだけでなく
論理計算の役割。 ( アロンゾ教会、1932 )
一般的に言えば、ラムダ計算は「すべての自尊心のあるプログラマーが知っておくべき」主題には適用されません。 これは非常に理論的なことであり、型システムを学習する場合や独自の関数型プログラミング言語を作成する場合、その研究が必要です。 それでも、HaskellやMLなどの中心にあるものを理解したい場合は、「アセンブリポイントをシフト」してコードを記述するか、単に視野を広げてください。
歴史への伝統的な(しかし短い)遠足から始めます。 前世紀の30年代、数学者は、デイビッドヒルバートによって定式化された、いわゆる解決問題 ( Entscheidungsproblem )に直面しました。 その本質は、私たちが何らかの声明を書くことができる特定の正式な言語を持っていることです。 有限数のステップでその真偽を判断するアルゴリズムはありますか? その答えは、当時のアロンゾ教会とアランチューリングの 2人の偉大な科学者によって発見されました。 彼らは(最初-彼によって発明されたλ計算の助けを借りて、そして2番目-チューリング機械の理論を使って)算術ではそのようなアルゴリズムは原則として存在しない、すなわち Entscheidungsproblemは一般的に不溶性です。
そのため、ラムダ計算は最初に大声で宣言されましたが、数十年間は数理論理学の特性であり続けました。 これまで、60年代半ばに、 ピーターランディンは、コアを小さな基本計算として定式化し、言語の最も重要なメカニズムを表現し、その動作を基本計算言語に翻訳することで表現できる便利な派生形式のセットで補完することで、複雑なプログラミング言語が学習しやすいことに注意していませんでした。 ランディンは、そのような基礎として教会のラムダ計算を使用しました。 そしてすべてをまとめて......
λ計算:基本概念
構文
ラムダ計算の基礎は、すべてのプログラマーに知られている概念、つまり匿名関数です。 組み込みの定数、基本演算子、数値、算術演算、条件式、サイクルなどはあり
最も単純な形式、純粋な型なしラムダ計算を検討します。これはまさに私たちが自由に使えるものです。
条件 :
| 変数: | x
|
| ラムダ抽象化(無名関数): | λx.t
、ここで x
は関数の引数、 t
はその本体です。 |
| 機能の適用(アプリケーション): | fx
( f
は関数、 x
はそれに代入される引数の値) |
運用優先契約 :
- この関数の使用は左結合です。 つまり
stu
は(st) u
と同じです
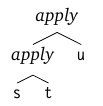
- アプリケーション(指定された値に関連するアプリケーションまたは関数呼び出し)は、到達するすべてのものを受け取ります。 つまり
λx. λy. xyx
λx. λy. xyx
はλx. (λy. ((xy) x))
と同じ意味λx. (λy. ((xy) x))
λx. (λy. ((xy) x))
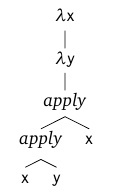
- 括弧は、アクションのグループ化を明示的に示します。
いくつかの引数を持つ関数には特別なメカニズムが必要なように思えるかもしれませんが、実際はそうではありません。 実際、純粋なラムダ計算の世界では、関数によって返される値も関数になる可能性があります。 したがって、元の関数を引数の1つだけに適用し、他の引数を「フリーズ」できます。 結果として、前の引数が適用される引数の「テール」から新しい関数を取得します。 このような操作はカリー化と呼ばれます ( Haskell Curryに敬意を表して)。 次のようになります。
f = λx.λy.t
| 2つの引数x
と y
および本体 t
持つ関数 |
fvw
| v
と w
を f
置き換える |
(fv) w
| このエントリは前のものと似ていますが、括弧は置換シーケンスを明確に示しています |
((λy.[x → v]t) w)
| x
代わりに v
を x
ます。 [x → v]t
は、「 x
すべての出現が v
置き換えられた本体 t
」を意味します |
[y → w][x → v]t
| y
代わりに w
を y
ます。 変換が完了しました。 |
そして最後に、スコープに関するいくつかの言葉。 変数
x
は
t
λ抽象化
λx.t
本体
t
場合、 バインドと呼ばれ
λx.t
x
重なる抽象化によって接続されていない場合、 freeと呼ばれます。 たとえば、
xy
および
λy.xy
での
x
の出現
λy.xy
自由であり、
λx.x
および
λz.λx.λy.x(yz)
での
x
の出現は接続されています。
(λx.x)x
最初のオカレンスが接続され、2番目のオカレンスは自由です。 用語内のすべての変数が接続されている場合、それはclosedまたはcombinatorと呼ばれます。 次の単純なコンビネータ( 恒等関数 )を使用します:
id = λx.x
アクションを実行しませんが、変更せずに引数を返します。
計算プロセス
次の用語の適用を検討してください。
(λx.t) y
その左側-
(λx.t)
-は、1つの引数
x
と本体
t
持つ関数です。 計算の各ステップでは、
t
内の変数
x
すべての出現を
y
に置き換えます。 このタイプの用語適用はredexと呼ばれ( 還元可能式から、 redex- 「短縮式」)、指定されたルールに従って書き換え書き換え操作はbeta reductionと呼ばれます。
次の計算ステップでredexを選択するためのいくつかの戦略があります。 例として次の用語を使用してそれらを検討します。
(λx.x) ((λx.x) (λz. (λx.x) z))
、
簡単にするために次のように書き直すことができます
id (id (λz. id z))
(
id
は
λx.x
の形式の恒等関数であることを
λx.x
)
この用語には3つのredexeが含まれます。
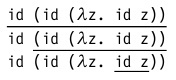
- 完全なβ還元 。 この場合、計算された用語内のredexが任意に選択されるたびに。 つまり この例は、内部redexから外部まで計算できます。

- 計算の通常の順序 。 最初は常に一番左、一番外側のredexです。
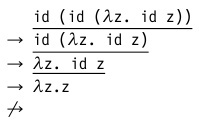
- 名前で呼び出します。 この戦略の計算手順は前のものと似ていますが、抽象化内の略語の禁止が追加されています。 つまり この例では、最後から2番目のステップで停止します。

Haskellは、このような戦略の最適化されたバージョン( 必要に応じて呼び出す )を使用します。 これらは、いわゆる「遅延」計算です。
- 値で呼び出します 。 ここでは、左端(外側)のredexから削減が始まります。これは、右側に値があります -これ以上計算できないクローズドターム。
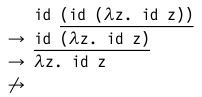
純粋なラムダ計算では、そのような用語はλ抽象化(関数)であり、より豊富な計算では、定数、文字列、リストなどになります。 この戦略は、すべての引数が最初に計算され、次にすべてが一緒に関数に代入されるときに、ほとんどのプログラミング言語で使用されます。
用語にredexがなくなった場合、 計算された 、または通常の形式であると言われます。 すべての用語が通常の形式を持っているわけではありません。たとえば、計算の各ステップで
(λx.xx)(λx.xx)
が生成されます(ここで、最初のブラケットは匿名関数で、2番目はプレース
x
代入される値です)。
値ベースの呼び出し戦略の欠点は、ループが発生し、用語の既存の通常の値が見つからない場合があることです。 たとえば、次の式を考えます
(λx.λy. x) z ((λx.xx)(λx.xx))
2番目の引数にはそのような形式がないという事実にもかかわらず、この用語は標準形式
z
持っています。 その計算では、値による呼び出し戦略はハングしますが、名前による呼び出し戦略は最も外部の用語から開始され、そこで2番目の引数は原則として不要であると判断します。 結論:redexに通常の形式がある場合、「遅延」戦略は間違いなくそれを見つけます。
別の微妙な点は、変数の命名に関連しています。 たとえば、置換後の項
(λx.λy.x)y
は
λy.y
で計算され
λy.y
つまり 変数名が一致するため、本来意図されていなかったアイデンティティ関数を取得します。 実際、ローカル変数を
y
ではなく
z
と呼びます。元の項は
(λx.λz.x)y
形式を持ち、縮小後は
λz.y
ようになります
λz.y
この種のあいまいさを排除するには、置換後も初期用語のすべての自由変数が自由なままであることを明確に監視する必要があります。 この目的のために、 α-変換を使用します-名前の競合を避けるために、抽象的に変数の名前を変更します。
また、抽象化
λx.tx
があり、
x
には本体
t
空きエントリがないこともあります。 この場合、この式はちょうど
t
と同等になります。 このような変換はη-変換と呼ばれます。
これで、ラムダ計算の概要は終わりです。 次の記事では、それが何であるかということに焦点を当てます:λ計算でのプログラミング。