2月17日、手紙に新しい亀裂が入りました。 この記事で説明するのは、彼の決定についてです(それだけではありません)。
亀裂のパラメーターは同じです。
- ファイル: ZeroNightsCrackMe.exe
- プラットフォーム: Windows 7(64ビット)
- パッカー:なし
- 反デバッグ:ぶつからない
- 解決策:メール/シリアル有効ペア
ツール:
- OllyDbg 2.01
- いくつかの灰白質
ソリューションに取り掛かりましょう...
狩りに行く
いつものように、実験を開始し、表面分析を実施します。 この反応は、過去の亀裂に似ています。

図 1
き裂のある過去の仕事の原理を知って、私たちはキーポイントの検索に進み、見つけます:
- 入力データを処理する関数。
- 検証テーブル検証アルゴリズム。
- 検証テーブル。
- 検証テーブルに記入するためのアルゴリズム。
- 検証テーブルに記入するためのアルゴリズムのデータ。
- シリアルコードを内部表現に変換するアルゴリズム。
- 変換表。
- 有効な文字範囲。
次に、すべてのキーポイントを以前のバージョンと比較して、違いを見つけます。
動物の道に沿って
入力処理機能
まず、入力されたデータを処理する機能を見つけます。 これは非常に簡単です。 逆アセンブラウィンドウを右クリックし、 「=>すべての参照文字列を検索」を選択します。

図 2
次に、 「Good work、Serial is valid !!!」という行をクリックして、ここにアクセスします。
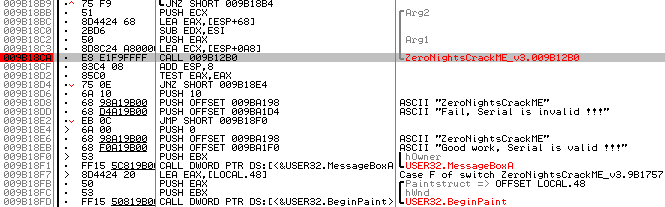
図 3
目的の関数はより高くなります(私の場合、 CALL 0x9b12b0です )。 3つのパラメーターが彼女に渡されます。 Arg2 、 Arg1では、シリアルコードのサイズとシリアルコードへのポインターがそれぞれ送信され、 ECXでは、電子メールへのポインターが登録されます。
検証テーブル検証アルゴリズム
関数の内部に入り、一番下に目を向けると、検証テーブルをチェックするためのアルゴリズムがあります(古いバージョンと同じです):

図 4
検証テーブルのアドレス
アルゴリズムの最初にブレークポイントを設定し、実行時にクラックを実行します(もちろん、データを入力して[ チェック ]ボタンをクリックした後)。

図 5.テストデータを入力します
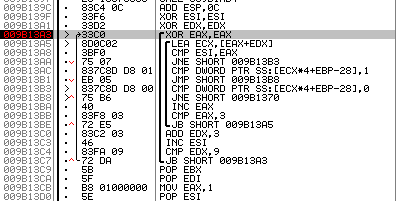
図 6.検証テーブルで停止
次に、テーブル自体のアドレスを決定します。 これを行うには、 「CMP DWORD PTR SS:[ECX * 4 + EBP-28]、1」という行に移動して、宛先アドレスを調べます。
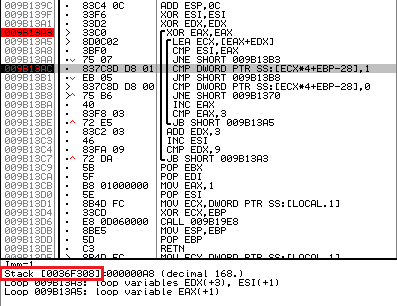
図 7.検証テーブルのアドレスの決定
私の場合、テーブルのアドレスは0x36f308 (赤で強調表示)です。

図 8.検証テーブルダンプ
検証テーブル充填アルゴリズム
過去の亀裂を解くときに実証されたのと同じ方法でアルゴリズムを検索します。
- クラックを続行します(OlkaでF9を押します)。
- 入力データ処理関数の内訳を示します。私の場合はCALL 9b12b0です(図3)。
- クラックに切り替え、ポップアップウィンドウ(成功または失敗の話)で[OK]をクリックします(これにより、クラックの処理を続行します)。
- 次に、「チェック」ボタンをクリックしてシリアル番号の再カウントを開始します。その後、コールCALL 0x9b12b0で停止する必要があります。
- 呼び出しCALL 0x9b12b0の上に立って、レコードのアドレス0x36f308にブレークを置きます。
- そして、もう一度F9を押します。
すべてが正しく行われた場合、ここに表示されます。

図 9.検証テーブルに記入するためのアルゴリズム
新しいアルゴリズムと古いアルゴリズムを比較すると、それらが異なることに気付くでしょう。

図 10.古いアルゴリズム( 前回の記事のスクリーンショット)
Pythonでの「新しいアルゴリズム」のプレゼンテーションは次のとおりです。
def create_table(first_part, second_part): result = [] curr_second = 0 out_index = 0 while(out_index < 3): inner_index = 0 while(inner_index < 3): curr_first = 0 accumulator = 0 index = 0 while(index < 3): first = first_part[inner_index + curr_first] second = second_part[index + curr_second] hash = 0 if (first != 0): while (first != 0): if (first & 1): hash ^= second second += second first = first >> 1 accumulator ^= hash index += 1 curr_first += 3 result.append(accumulator & 0xff) inner_index += 1 out_index += 1 curr_second += 3 return result
このアルゴリズムで使用されるデータの検索に移りましょう。
検証テーブルに記入するためのアルゴリズムのデータ
アルゴリズムコードを分析した後、その操作のデータが由来する2つの場所が見つかりました。
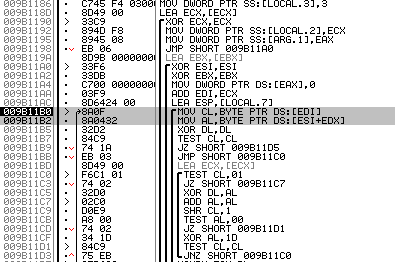
図 11.新しいアルゴリズムが動作する配列
それらは灰色の長方形で強調表示されます。 私の場合、アドレス0x9b11b0および0x9b11b2で、次の配列にアクセスしています:
- 0x00758628(図12)
- 0x00758908(図13)

図 12

図 13
各配列には、それぞれ1バイトの9つの要素が含まれます。
古いクラックを解決する場合、シリアルコードを内部表現に変換するアルゴリズムを検索しますが、新しいクラックでは、古いクラックの動作との大きな違いが見つかりました。そのため、違いに関する情報は次のとおりです。
古いバージョンと新しいバージョンの違い
古いバージョンでは、クラックはシリアルコードで次のように機能していました。
- シリアルコードは2つの部分に分割されました。
- 各部分は内部表現に変換されました。
- 次に、各部分を混合(混合)しました。
- その後、両方の部分が検証テーブルに記入するためのアルゴリズムに転送されました。
最終的に、次のようなものが得られました。
Serial |- part_1 |- part_2 part_1 = intermediate_view(part_1) part_2 = intermediate_view(part_2) part_1 = mix(part_1) part_2 = mix(part_2) valid_table = algo(part_1, part_2)
新しいバージョンでは、事態は少し複雑になりました。
- シリアルコードは2つの部分に分かれています。
- その各部分は内部表現に変換されます。
- 最初の部分+固定配列(3、5、7、5、7、3、7、3、5)がアルゴリズムに転送されます。
- 2番目の部分+固定配列(3、5、7、5、7、3、7、3、5)はアルゴリズムに転送されます。
- 項目3〜4の結果は、検証テーブルに記入するためのアルゴリズムに渡されます。
その結果、次のような結果が得られます。
Serial |- part_1 |- part_2 part_1 = intermediate_view(part_1) part_2 = intermediate_view(part_2) part_1 = mix(part_1) part_2 = mix(part_2) salt = [3, 5, 7, 5, 7, 3, 7, 3, 5] part_a = algo(part_1, salt) part_b = algo(part_2, salt) valid_table = algo(part_a, part_b)
固定配列に依存することになります。
シリアルコードを内部表現に変換するアルゴリズム
シリアルコードコンバーターの検索はお任せしますが、ここでは行いません。 古いバージョンと同じ方法で検索できます。
変換表と有効範囲
テーブルと有効範囲は古いバージョンと同じです。
待ち伏せのための繁殖地の準備
必要な要素がすべて揃ったので、決定を進めることができます。
アクションのアルゴリズムは次のとおりです。
- algo(part_a、part_b)の場合、結果[ 1、0、0、0、1、0、0、0、0、1]を与えるpart_aとpart_bを見つけます
- part_a = algo(part_1、salt)の場合、 part_aと等しい結果を生成するpart_1を見つけます。
- part_b = algo(part_2、salt)の場合、 part_bと等しい結果を生成するpart_2を見つけます。
アルゴ(part_a、part_b)から始めましょう
最初の記事を読んだ場合、必要なテーブル[ 1、0、0、0、1、0、0、0、1]をコンパイルするには、 「ゼロ "または"ユニット " 。
古いバージョンのクラックでは、これらのバイトを見つけるのは非常に簡単でした。 実行する必要があるのは、使用可能なアルファベット全体を並べ替え、いくつかの簡単な操作をそれに適用することだけでした。
新しいバージョンでは、これを行うのははるかに困難です(ただし、これは一見しただけで、以下で理由を説明します)。 古いバージョンでは、1つの要素を反復処理できました。 新しいバージョンでは、3つの要素はすべて相互接続されているため、3つの要素を反復処理する必要があります。
それで、なぜ新バージョンは一見複雑なように見えるのでしょうか?
最初の記事では、「ゼロ」と「ユニット」の検索の背後に実際に隠されていた「魔法」を明らかにしなかったためです(この記事では、明らかにする必要がありますが、これはできません)。 私のkeygenでは、必要な「ゼロ」と「1」を検索する関数を使用しましたが、完全に明白な方法ではありませんでした。 これは、最も好奇心をそそり、それらを単一のケース(最初のケースはクラック)のパスに沿って配置することに成功しました。 彼らが(今のように)もう1つのクラックを与えられたが、異なるアルゴリズムを使用すると、彼らは「ゼロ」と「1」を検索する新しい方法を考え出す必要があり、それは多くの人に起こったようです;)
まあ、わかりました、少ない言葉はより多くのビジネスです。
以下は、すべてのヌル文字と単一文字を見つけるのに役立つ魔法の「呪文」です。
data_zero, data_ones = [], [] for a in range(0, 256): part_a = [a, a, a, a, a, a, a, a, a] part_b = [a, a, a, a, a, a, a, a, a] result = create_table(part_a, part_b) if result == [0, 0, 0, 0, 0, 0, 0, 0, 0]: data_zero.append(a) elif result == [1, 1, 1, 1, 1, 1, 1, 1, 1]: data_ones.append(a) print("ZERO:", data_zero) print("ONES:", data_ones)

図 14
さて、「ゼロ」と「1」を与える要素のグループがあります。 目的のテーブル[1、0、0、0、1、0、0、0、1]を取得する方法は?
最も気配りのある/独創的な人は、互いに乗算すると、単位行列[1、0、0、0、0、1、0、0、0、を与えるべき行列を扱っていることに気付くことができます(たとえば、 前の記事のコメントから) 1]。 したがって、単位行列を取得するには、2つの単位行列または2つの逆行列が必要です。
必要な単位マトリックスを取得するには、次のパターンを使用できます。
# part_a = [y, x, x, x, y, x, x, x, y] part_b = [y, x, x, x, y, x, x, x, y] result = algo(part_a, part_b)
yの代わりに-任意の1文字を置換し、 xの代わりに-任意のゼロを置換します。
他のパターンを使用できます。次の「スペル」を使用してそれらを見つけることができます。
happy = [1,32] for byte_1 in happy: for byte_2 in happy: for byte_3 in happy: for byte_4 in happy: for byte_5 in happy: for byte_6 in happy: for byte_7 in happy: for byte_8 in happy: for byte_9 in happy: part_1 = [byte_1, byte_2, byte_3, byte_4, byte_5, byte_6, byte_7, byte_8, byte_9] part_2 = [byte_1, byte_2, byte_3, byte_4, byte_5, byte_6, byte_7, byte_8, byte_9] result = create_table(part_1, part_2) if result == [1, 0, 0, 0, 1, 0, 0, 0, 1]: print("%s | %s " % (part_2, part_1))

図 15
置換後、たとえば次のパターンを取得できます。
patterns = [ # Pattern 0 [ [y1, x1, x1, x1, y2, x1, x1, x1, y3], [y1, x1, x1, x1, y2, x1, x1, x1, y3] ], # Pattern 1a [ [y1, x1, x1, x1, x1, y1, x1, y1, x1], [y1, x1, x1, x1, x1, y1, x1, y1, x1] ], # Pattern 1b [ [y1, x1, x2, x3, x4, y1, x5, y1, x6], [y1, x2, x1, x5, x6, y1, x3, y1, x4] ], # Pattern 2a [ [y1, x1, x1, x1, y1, x1, x1, x1, y1], [y1, x1, x1, x1, y1, x1, x1, x1, y1] ], # Pattern 2b [ [y1, x1, x2, x3, y2, x4, x5, x6, y3], [y1, x1, x2, x3, y2, x4, x5, x6, y3] ], # Pattern 3a [ [x1, x1, y1, x1, y1, x1, y1, x1, x1], [x1, x1, y1, x1, y1, x1, y1, x1, x1] ], # Pattern 3b [ [x1, x2, y1, x3, y2, x4, y3, x5, x6], [x6, x5, y3, x4, y2, x3, y1, x2, x1] ], # Pattern 4a [ [x1, y1, x1, y1, x1, x1, x1, x1, y1], [x1, y1, x1, y1, x1, x1, x1, x1, y1] ], # Pattern 4b [ [x1, y1, x2, y2, x3, x4, x5, x6, y3], [x3, y2, x4, y1, x1, x2, x6, x5, y3] ], # Pattern 5 [ [x1, x2, y1, y2, x3, x4, x5, y3, x6], [x4, y2, x3, x6, x5, y3, y1, x1, x2] ] ]
必要なIDマトリックス(つまり、検証テーブル)を取得する方法がわかったので、他の問題に進みます。
適切なpart_aおよびpart_bを選択する方法
次のことを知っています。
part_a = algo(part_1, salt) part_b = algo(part_2, salt) valid_table = algo(part_a, part_b)
たとえば、 part_aはpart_1とsaltに依存します。 次に、 part_aの可能な組み合わせを絞り込みます。 論理的な疑問が生じます。
どの組み合わせを使用できますか?
多くの人はすでに何をする必要があるかを推測していると思いますか そうです、次の「スペル」を使用してください!
それらの1つを次に示します。
# serial_data email “support@reverse4you.org” serial_data = [52, 233, 91, 105, 65, 15, 50, 176, 90, 40, 225, 81, 207, 79, 34, 19] def get_items(first_part, second_part): result = [] inner_index = 0 while(inner_index < 3): curr_first = 0 accumulator = 0 index = 0 while(index < 3): first = first_part[inner_index + curr_first] second = second_part[index] hash = 0 if (first != 0): while (first != 0): if (first & 1): hash ^= second second += second first = first >> 1 accumulator ^= hash index += 1 curr_first += 3 result.append(accumulator & 0xff) inner_index += 1 return result a = 0x3 b = 0x5 c = 0x7 first_part = [a, b, c, b, c, a, c, a, b] second_part_new = [0, 0, 0] count = 0 result_table = [] for byte_1 in serial_data: second_part_new[0] = byte_1 for byte_2 in serial_data: second_part_new[1] = byte_2 for byte_3 in serial_data: second_part_new[2] = byte_3 res = get_items(first_part, second_part_new) print("index: %s, table: %s" % (count, res)) count += 1 print("Count: %s" % count)
「スペル」が正常に機能する場合、 part_aおよびpart_bで使用できるオプションは4096のみです (より正確には、「オプションの下」)。

図 16
これで、最初の有効なキーを生成するためのすべてのデータができました。 もちろん、内部表現を持つバイトを使用していることを忘れないでください。つまり、クラックでウィンドウに入力する前に、バイトを通常の外観に戻す必要があります。
最初の被害者(最初の有効なキー)
注意しておけば、4096のすべてのオプションを「すべての要素が偶数」と「すべての要素が偶数」の 2つのグループに分けることができることに気づいたでしょう。
インデックス:0035、テーブル: [116、222、172] <=すべての要素は偶数
インデックス:0560、テーブル: [ 172、116、222 ] <=すべての要素が偶数
インデックス:0770、テーブル: [ 222、172、116 ] <=すべての要素が偶数
インデックス:0117、テーブル: [ 1、229、111 ] <=すべての要素が偶数ではありません
インデックス:1287、テーブル: [229、111、1] <=すべての要素が偶数ではありません
インデックス:1872、テーブル: [111、1、229] <=すべての要素が偶数ではありません
ただし、利用可能な「パターン」を見ると、「オプション」のそれぞれに「偶数」要素と「偶数ではない」要素の両方が必要であることがわかります。
以下に、アイデンティティを与える2つのマトリックスを示します。
part_a
[176、176、65] <=偶数と偶数はありません
[176、65、176] <=偶数と偶数はありません
[65、176、176] <=偶数と偶数はありません
part_b
[176、176、65] <=偶数と偶数はありません
[176、65、176] <=偶数と偶数はありません
[65、176、176] <=偶数と偶数はありません
valid_table = part_a * part_a
[1、0、0]
[0、1、0]
[0、0、1]
「偶数」要素と「偶数」要素を持つ「オプション」がないため、クラックにエラーがあると結論付けます。 論理的な疑問が生じます。
間違いは何ですか?
簡単に考えた後、エラーは固定行列[0x3、0x5、0x7、0x5、0x7、0x3、0x7、0x3、0x5]にあると結論付けました。 偶数と奇数の「オプション」を取得するには、 「0x3」 、 「0x5」 、 「0x7」をそれぞれ「0x2」 、 「0x3」 、 「0x8」に置き換えるか、2つの偶数要素と1つの奇数要素がある別のオプションに置き換える必要があります。たとえば、そのような"0x4" 、 "0x7"および"0x8" (オプションとして)。
このエラーはカスペルスキーに報告されました。 彼らは、(現在調査中の)バージョンはドラフトであると言った。 その後、同日、エラーのないバージョンが全員に送信されました。 確かに、新しいバージョンでは固定テーブルがなく、これよりも簡単に解決されましたが、これについてはボーナスセクションで少し後で説明します:)
正しい置換を実行したことを確認するには(たとえば、 「0x2」 、 「0x3」 、 「0x8」以外の文字を挿入することにした場合)、次の「スペル」を使用する必要があります。
serial_data = [52, 233, 91, 105, 65, 15, 50, 176, 90, 40, 225, 81, 207, 79, 34, 19] a = 0x2 b = 0x3 c = 0x8 first_part = [a, b, c, b, c, a, c, a, b] second_part_new = [0, 0, 0] count = 0 result_table = [] for byte_1 in serial_data: second_part_new[0] = byte_1 for byte_2 in serial_data: second_part_new[1] = byte_2 for byte_3 in serial_data: second_part_new[2] = byte_3 res = get_items(first_part, second_part_new) print("index: %s, table: %s" % (count, res)) if (res[0] % 16 == 0 and res[1] % 16 == 0 and res[2] % 16 == 1) or\ (res[0] % 16 == 1 and res[1] % 16 == 0 and res[2] % 16 == 0) or\ (res[0] % 16 == 0 and res[1] % 16 == 1 and res[2] % 16 == 0): result_table.append(res) count += 1 print("Count:", count) print("Good:", result_table)
ベイトが正しく選択された場合(この例では「0x2、0x3、0x8」)、トラップ(「Good」フィールド)には少なくとも1つのビースト(3つのアレイで構成されるグループ)があります。 固定マトリックス(要素「0x2」、「0x3」、「0x8」)の出力例を以下に示します。

図 17
ご覧のとおり、幸運が私たちに微笑んだので、私たちのtrapには3匹もの野生動物がいましたが、これはもちろんお祝いテーブルを設定するのに役立ちます(つまり、 part_aとpart_bを形成するために使用できます)。
最も注意深い人は、 「Good」行の出力をグループに分割できることにすでに気付いています。各グループには3行あります。
[0、144、81]
[81、0、144]
[144、81、0]
[144、145、0]
[0、144、145]
[145、0、144]
[0、144、209]
[209、0、144]
[144、209、0]
さらに注意深いのは、これらすべての文字が「ゼロ」と「単一」の文字のセットに含まれていることにおそらく気づいたでしょう。

図 18
まあ、最も独創的な(私は願っています)既に大きなテーブルでごちそうです、彼らは大きな獣を追跡することができたので、同様の「呪文」で彼を誘います:
# # [0, 144, 209] # [209, 0, 144] # [144, 209, 0] a = 144 b = 209 c = 0 # part_a = [c, a, b, b, c, a, a, b, c] part_b = [a, b, c, c, a, b, b, c, a] # part_a1 = [0, 144, 209] # part_a2 = [209, 0, 144] # part_a3 = [144, 209, 0] # part_a = part_a1 + part_a2 + part_a3 # part_b1 = [144, 209, 0] # part_b2 = [0, 144, 209] # part_b3 = [209, 0, 144] # part_b = part_b1 + part_b2 + part_b3 result = create_table(part_a, part_b) print(result)
これは、クラックでこれを解決する場所です...内部バイトをクラックに入れてウィンドウに入力できるように内部バイトを通常に変換する方法は、あなたが自分で理解すると思います。
それまでの間、新しい(修正された)クラックの検討を進めます。 特定のクラックについて調べたすべてが新しいものに関連していることをすぐに言いたいので、その動作の原理の表面的な説明に限定し、keygenへのリンクを提供します(より好奇心が強い、またはその逆)。
ボーナス(keygen +新しいクラックの説明)
利用可能なバージョンと混同しないように、番号付けを明確にします。
- ZeroNightsCrackMe_v1- こちらでレビュー。
- ZeroNightsCrackMe_v2-ドラフトバージョンであり、この記事の上記で説明されています。
- ZeroNightsCrackMe_v3-以下で表面的にレビュー+ keygenが提供されます。
検証テーブル検証アルゴリズムと検証テーブル自体
v1およびv2の以前のすべてのバージョンと同様。
検証テーブル充填アルゴリズム
v2のドラフトバージョンと同様(この記事で前述)。
検証テーブルに記入するためのデータ
動作原理はv1の最初のバージョンと同じですが、他のミキサーが使用されます。
シリアルコードを内部表現、変換テーブル、有効範囲に変換するアルゴリズム
v1およびv2の以前のすべてのバージョンと同様。
新しいバージョンのKeygen
このスレッドには、バージョンv2およびv3のクラックがあります 。 また、 Darwinからv3の新しいバージョンのkeygenが見つかります。
Keygen アーカイブパスワード: Darwin_1iOi7q7IQ1wqWiiIIw
クラックの3番目のバージョンのkeygenを確認します。
> keygen_v3.py habrahabr.ru> result.txt
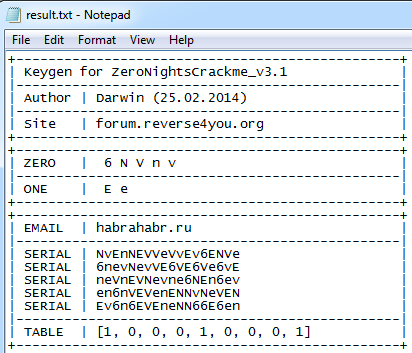
図 19
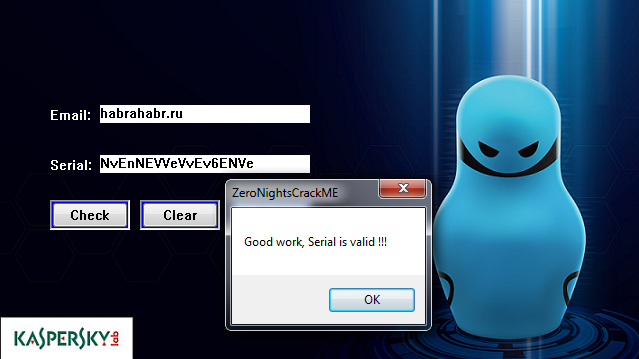
図 20
最後に感謝します。 じゃあね!