
リードソロモンコードは、非バイナリ、ブロック、ノイズ耐性コードを指し、破損した情報の損失を回避するために情報ストレージの分野で使用できます。
リードソロモンコードを使用して情報をコーディングすることに専念するハブに関する投稿がありますが、例として、著者は単純なガロア体を使用しています。 この記事では、拡張ガロア体、特にGF(2 ^ m)を使用した作業について説明します。これはデジタル情報に合理的に使用されます。 エンコード、デコード、エラー修正の私の同様の実装は、 ここにあります 。
リードソロモンコードを使用する場合、冗長文字の割合は、回復可能なデータ量の2倍です。 例で説明しましょう:10文字のシーケンスがあり、そのうち3文字(元の情報の30%)でエラーを回復できるようにしたい場合、10 + 3 * 2 = 16文字を保存する必要があります。 各変数に名前を付けます:n = 10、情報シンボルの数。 f = 3、回復可能な文字の数。 g = 16、エンコードされたシーケンスの長さ。 したがって、式は次のように記述できます。g= n + f * 2。
フィールズガロア
データのエンコードおよびデコード時に情報を処理するために、すべての算術演算はガロア体で実行されます。 いわゆる多項式演算またはガロア体の演算が適用されます。 したがって、操作の結果もこのフィールドの要素になります。 特定のガロア体は、固定範囲の数値で構成されています。 フィールド特性は、ある素数pと呼ばれます。 フィールドの順序、つまり その要素の数は、特定の自然な特性pmであり、m∈Nです。 m = 1の場合、フィールドはシンプルと呼ばれます。 m> 1の場合、体の形成のために、次数mの生成多項式も必要です;そのような体は拡張と呼ばれます。 GF(p ^ m)はガロア体の指定です。
デジタルデータを操作するには、フィールド特性としてp = 2を使用するのが自然です。 m = 1の場合、コードシーケンスの要素はビットになり、m = 8-8ビットの場合、つまりバイトになります。 実際、バイトで動作するリードソロモンコードが最も一般的です。
エンコードおよびデコード操作に進む前に、GF(2 ^ 3)の例を使用してガロア体の算術を理解します。 このフィールドは、0〜7の数字で構成されます。
加算操作
最も単純なのは加算演算で、2を法とする単純なビット単位加算(XOR)です。
例:5 + 3 = 110 = 6
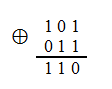
乗算演算
残念ながら、乗算の演算ははるかに複雑です。乗算を実行するには、数値を多項式に変換する必要があります。
例:5 = 101 = 1∙x ^ 2 + 0∙x ^ 1 + 1∙x ^ 0 = x ^ 2 + 1
ご覧のとおり、多項式形式の数値は、係数が数値のバイナリ表現の桁の値である多項式です。
多項式形式で2つの数値を乗算します。
5∙7 =(x ^ 2 + 1)∙(x ^ 2 + x + 1)= x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 = x ^ 4 + x ^ 3 + x + 1 = 11011 = 27
そのため、まず、多項式形式でも加算はモジュロ2で実行されるため、x ^ 2 + x ^ 2 = 0であることに注意してください。 第二に、乗算27の結果は、使用済みフィールドGF(2 ^ 3)に含まれません(上記のように、0から7までの数字で構成されます)。 この問題に対処するには、生成多項式を使用する必要があります。 生成多項式は既約、つまり単純です(素数との類推により、1で割り切れます)。 ガロア体の算術では、既約多項式は素数の類似体です。 たとえば、生成多項式f(x)= x ^ 3 + x + 1を使用します。
また、xは式f(x)= x ^ 3 + x + 1 = 0を満たすと仮定されます。
乗算の例に戻ります。

同じ結果は、生成多項式を乗算することで得られる多項式の除算の剰余として取得できます。
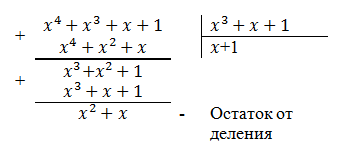
乗算表を作成しましょう:
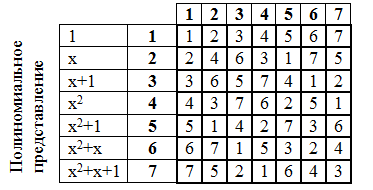
分割運用
多項式形式の除算の動作を理解することは可能ですが、それはかなり困難です。 したがって、乗算表に従って実装することをお勧めします。
例:6÷5 = 7
非常に重要なのは、ガロア体の要素の次数の表です。 累乗も、乗算と同様に多項式形式で実行されます。
例:5 ^ 2 =〖(x ^ 2 + 1)〗^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 = x∙(x ^ 3 + x + 1)= x ^ 2 + x + 1 = 111 = 7
したがって、度のテーブルをコンパイルします。

次数テーブルは循環的です。7番目の次数はゼロに対応するため、8番目は1番目に対応します。 必要に応じてこれを確認できます。
ガロア体には、原始項の概念があります。つまり、次数に体のすべての非ゼロ要素が含まれる体の要素です。 度の表を見ると、すべての要素がこの条件に対応していることが明らかです(当然、1を除いて)。 ただし、常にそうであるとは限りません;たとえば、GFの度数表を示します(16)。
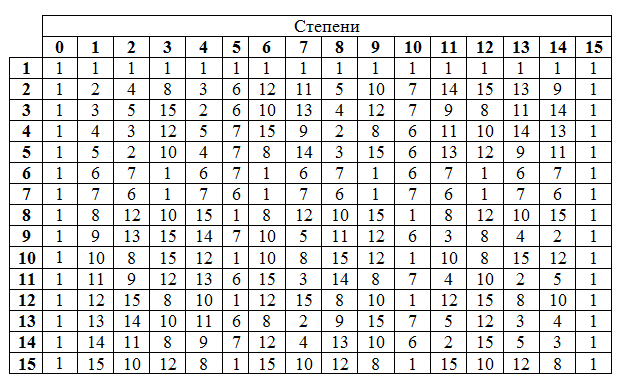
考慮しているフィールド、つまり特性2では、常に2を選択します。プリミティブメンバとして、そのプロパティを指定すると、フィールドの任意の要素をプリミティブメンバの次数で表すことができます。
例:5 = 26、7 = 25
このプロパティを使用し、次数テーブルの循環性を考慮して、数値の乗算を再度試みます。
5∙7 = 2 ^ 6∙2 ^ 5 = 2 ^(6 + 5)= 2 ^ 11 = 2 ^(11 mod 7)= 2 ^ 4 = 6
結果は以前に計算したものと一致しました。
それでは、分割を行いましょう:
6÷5 = 2 ^ 4÷2 ^ 6 = 2 ^(4-6)= 2 ^(-2)= 2 ^((-2)mod 7)= 2 ^ 5 = 7
得られた結果も真です。
さて、完全を期すために、累乗することを見てみましょう。
5 ^ 2 =(〖2 ^ 6)〗^ 2 = 2 ^(6∙2)= 2 ^ 12 = 2 ^(12 mod 7)= 2 ^ 5 = 7
繰り返しますが、予期せず同じ結果になりました。
このような乗算と除算のアプローチは、多項式を使用した実際の演算よりもはるかに単純であり、それらについては大きな乗算テーブルを格納する必要はなく、原始体項の次数の行だけを格納する必要があります。