
それでは、「シミュレーテッドアニーリング」に似たアルゴリズムをどの基準で比較できますか? 最もよく比較されたもの:
•効率
•作業速度
•メモリ使用量
そして、私は追加したいと思います
•再現性(つまり、結果のアルゴリズムの安定性を確認します)。
評価基準
最初の基準として、結果のルートの長さを使用します。 ランダムに生成されたポイントのセットに最適なルートが何であるかはわかりません。 どうする 簡単にするために、すべてを1つのセットで実行してみましょう。 結果の信頼性を高めるために、よりペダンティックなものをいくつかのセットに拡張し、結果を平均化できます。 その間、ファイルからテストセットの読み取り値を追加して、実験を繰り返すことができるようにする必要があります。
操作の速度を決定するために、Octaveにはこのような関数があるため、プロセッサがアルゴリズムに費やした時間を計算します。 もちろん、異なるコンピューターでは結果も異なります。 したがって、比較のために、常に実行される1つのアルゴリズムですべての結果をスケーリングできます。 たとえば、元の記事のアルゴリズムによると、彼は最初の記事を取得しました。
メモリの支出ですぐに何も思いつきませんでした。 したがって、指を把握しようとします。 私が理解しているように、著者の主な費用はインデックスの2つの配列です。 1つは現在のルート用、もう1つは候補ルート用です。 そして、もちろん、ポイントごとに2つの座標に沿ったルートポイントの配列。 残りのコストは、ランタイム環境ごとに異なり、テストデータのサイズに依存しないため、考慮されません。 (おそらくここで私はやや過酷ですが、提案に対して非常にオープンです)。 主な費用の合計はN * 4です。Nは回避するポイントの数です。
小さな余談:ここで説明するすべては、元の記事のようにMatLabではなく、Octave [http://www.gnu.org/software/octave/]でテストされました。 これにはいくつかの理由があります。まず、私はそれを持っています。次に、そのプログラミング言語はMatLabとほぼ完全に互換性があります。
分析しています...
開始するには、既存のコードとの互換性を確認してください(元の記事の最後にあるダウンロードリンク)。 すべてが機能しますが、美しいグラフィックスを生成するコードはありません。 重要ではありません-元のアルゴリズムを呼び出して結果を描画する関数を作成します。 それでも同じように、統計のコレクション全体をキット化する必要があります。
したがって、分析機能は次のとおりです。
function [timeUsed, distTotal] = Analyze( ) % load points_data.dat cities % timeStart = cputime(); % result = SimulatedAnnealing(cities, 10, 0.00001); % timeUsed = cputime - timeStart; % distTotal = PathLengthMat(result); % plot(result(:,1), result(:,2), '-*'); drawnow (); end
都市座標の配列を持つファイルを生成するための関数を作成しませんでした。 これは、コマンドラインから直接実行できます。
cities = rand(100, 2)*10; save points_data.dat cities;
はい、元のアルゴリズムのCalculateEnergy関数が評価に使用されていないことに気づいた場合、2つの理由があります。 第一に、他のメトリクスを試してみるというアイデアがありますが、それでもユークリッド距離で結果を評価する方が良いです。 そして第二に、元の記事の著者はユークリッド距離の計算を詳細に説明しましたが、ソースのコードはマンハッタンを計算します。 次のように正しく計算された2点のユークリッド:
function [dist] = distEuclid(A, B) dist = (A - B).^2; dist = sum(dist); dist = sqrt(dist); end
時々、結果の安定性を判断するために、このすべてをサイクルで何度も実行し、結果を収集して、結果の平均と広がりの程度を評価します。
function [] = Statistics testNum = 1000; % timeUsed = zeros(testNum,1); distTotal = zeros(testNum,1); for n=1:testNum [timeUsed(n), distTotal(n)] = Analyze; end % time = [mean(timeUsed), std(timeUsed)] dist = [mean(distTotal), std(distTotal)] end
最初の失望は、どれくらい時間がかかるかです! コンピューターコアi5-3450 3.1GHz 8Gb RAMでは、1つのパスが平均578秒で実行されます。 したがって、信頼性を高めるために1000サイクルを開始して平均したかったのですが、これは6.69日です。 100サイクル実行する必要があり、約16時間4分後(つまり午前中)に結果が得られました。
平均計算時間578.1926(サンプル3.056の標準偏差)、結果のパスの平均長91.0844(標準偏差2.49)。 つまり、すべてが安定しているため、使用に適しています。 しかし、どのくらい。 私は抵抗することができず、最適化を行いたくなりました。
最適化
加速度の最初の候補は距離推定です。 Octaveは、MatLabと同様に、マトリックスコンピューティング向けに最適化されています。これも同様に書き直します。 この関数は2つの配列を取ります。A-セグメントの始まり、B-それぞれの終わり:
function [dist] = distEuclid(A, B) dist = (A - B).^2; dist = sum(dist, 2); dist = sqrt(dist); dist = sum(dist); end
この関数を呼び出すために、ポイントの初期配列を周期的にシフトしてデータを準備し、セグメント終了の配列を取得する別の関数を導入します。
function [length] = PathLengthMat(cities) citiesShifted = circshift(cities, 1); length = distEuclid(cities, citiesShifted); end
もちろん、関数SimulatedAnnealingおよびGenerateStateCandidateを書き換えて、ポイント配列を直接操作する必要があります。 完全なコードは提供しません。最後に、興味のある人のためのすべてのソースコードを含むアーカイブへのリンクがあります。
始めましょう。平均計算時間は70.554(サンプルの標準偏差は0.096)、結果のパスの平均長は90.403(標準偏差2.204)です。
速度の増加は8倍以上です! さらに試してみるのはもはや面白くありません。そのような増加はありません。 確かに、(提案された方法論による)メモリ消費には、2つの座標(現在のソリューションと新しい候補)に2つのポイントの配列があります。つまり、N * 4です。 何も変わっていません。
ただし、アルゴリズムを評価しているため、温度データを確認します。 生成されたポイント配列の初期「エネルギー」の範囲は500〜700で、最終的な出力ルートは90プラス/マイナス5前後で変動します。アルゴリズムを1,000万に引き上げましたが、なぜアルゴリズムをチェックするときに自制する必要があるのですか?)。 実際、少し実験した結果、Tmax = 300とTmin = 0.001でほぼ同じ結果が得られました。 同時に、実行時間は21秒に短縮されました。
探索オプション
それでは、何かと比較してみましょう。 当初、マンハッタンのメトリックと比較するアイデアがありましたが、実装されたことが判明しました。 次に、この最適化があります。 要するに-マンハッタン距離の行列計算用のコードを追加して、試してください。 また、別の温度変化関数がどのように表示されるかも興味深いです。 元の記事で約束された温度変化関数の線形性にだまされた人々は、失望せざるを得ない-そうではない。 これを理解するには、彼女のスケジュールを見てください:
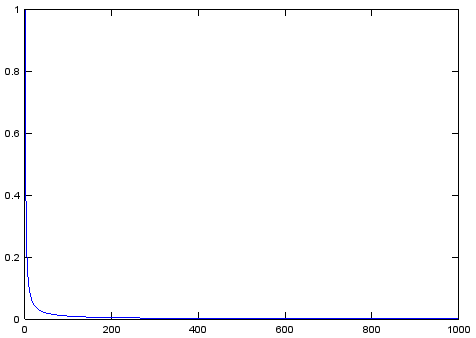
おそらく、科学で使用される他のすべてのオプションの分母は実際より悪く見えるため、関数の分母の線形性が意図されていました。
比較のため、温度関数T = Tmax *(A ^ k)も試してみます。ここで、Aは通常0.7〜0.999の範囲内で選択されます。 (実装された場合、欲張りではありません-Ti = A * Ti-1)。 「焼鈍」とその使用のオプションは「焼入れ」と呼ばれます。 最低温度までずっと速く低下しますが、初期段階ではより穏やかです。 つまり、アルゴリズムは最初はより多くの実験を行いますが、より速く終了します。 だから-結果の要約表:
| アルゴリズム | 長さ(スプレッド) | 時間(散布) | 記憶 |
|---|---|---|---|
| 記事から | 91.0844(2.4900) | 578.1926(3.0560) | N * 4 |
| ドットマトリックス(10-0.00001) | 90.4037(2.2038) | 70.554593(0.096166) | N * 4 |
| ドットマトリックス(300-0.001) | 90.7956(2.1967) | 20.94024(0.16235) | N * 4 |
| マトリックスマンハッタン(10-0.00001) | 90.0506(3.2397) | 70.96909(0.7807) | N * 4 |
| マトリックス「急冷」(300-0.001) | 92.0963(2.3129) | 22.59591(0.39581) | N * 4 |
結論
- アルゴリズムの結果を定量化する機能は、比較する人がいなくても便利です。
- プログラムの作成時にツールの機能を考慮すると、多くの時間を節約できます。
- 特定のタスクのパラメーターを選択した場合-もう少し節約できます。
- アルゴリズムを最適化せずに速度で比較することは無意味です-実行時間はほぼランダム変数になります。
- 最新のプロセッサでは、ルートを取得および抽出することはモジュールを取得するのとほぼ同じくらい簡単です。単純化することなく数学をゆがめて書くことができません。
- 1つのアルゴリズムの多くのバリエーションは、グラフォマニックではないにしても非常に近い結果をもたらします-より便利な(またはより馴染みのある)ものを使用してください。
約束されたソースはここにあります
まあ、あなたがそれを好きなら-あなたはしばらく後にそれを他のものと比較することができます。