ご注意
それでは始めましょう。
1.初期データ分析
この部分は、プロセスの最も重要な部分の1つです。なぜなら、今間違えた場合、残りの作業はすべて時間の無駄になる可能性があるからです。 前の記事で使用したモスクワ地域の倉庫群の1つで、商品の出荷に関するデータを開きます。 プロットしましょう:
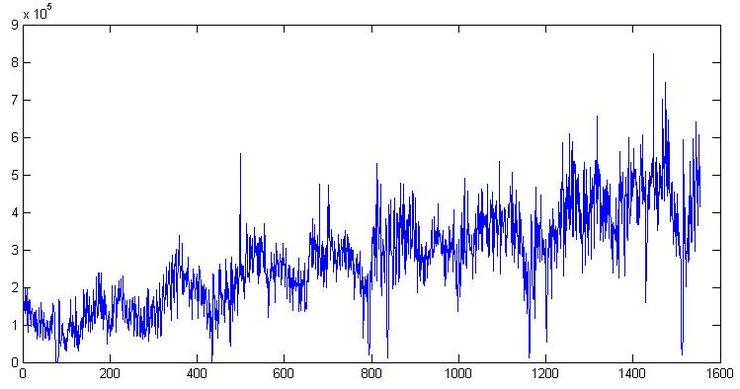
第一に、約300日のオーダーのトレンドとサイクルが明らかにあります。 チャートを閉じます。 煙を持って行きましょう。 来て、もう一度開いて、数字そのものを見てみましょう。 出荷日は2009年9月1日の形式で示されているため、Excelで開き、曜日を表示するためにデータを[$ -F800] dddd、mmmm dd、yyyyの形式に転送すると、通常、土曜日に出荷の値がはるかに少なくなります週の残りより。 たとえば、チャート1に2週間が示されています。一般的に、ローダー叔父のVasyaは土曜日の早い時間に家を出てサッカーを観戦しています。そのため、7日間の季節性を持つマイクロサイクルの存在をさらに考慮する必要があります。 ところで、前の記事のように週間隔にデータを転送するのではなく、毎日のデータを引き続き使用します。
図表1 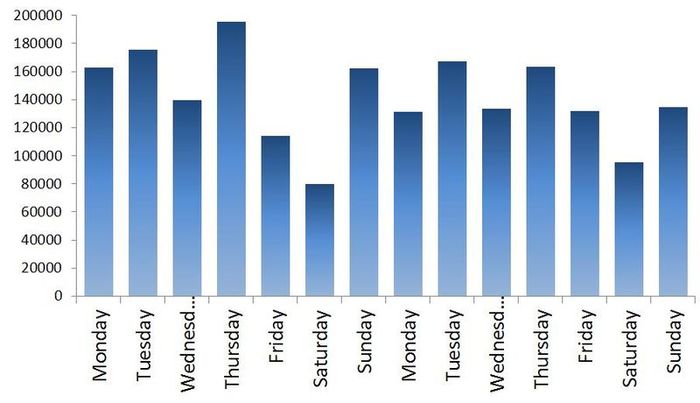

2.状態空間モード
ここで、最小限の理論、より詳細に、すべての式が由来する理由と場所を本で読むことができるか、コメントで答えます。
ある時系列があるとしましょう

どこで
トレンドは、ローカルの線形トレンドのモデルとして構築することにより多様化できます。
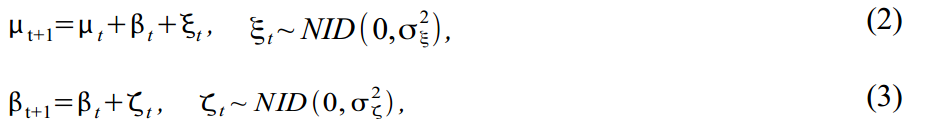
(2)はトレンド自体であり、(3)はトレンドスロープであり、それぞれにエラーがあります。 このようなモデルは、ドリフトランダムウォークから統合ランダムウォークモデルまで、トレンドモデリングに多くのオプションを提供します。 多くの計量経済学者は、(2)のエラーを除去して、滑らかで滑らかなトレンドを取得し、すべてのランダムエラーをトレンドスロープに割り当てます。
確率的サイクルは、三角関数とそれらの導関数の合計としてモデル化されます:
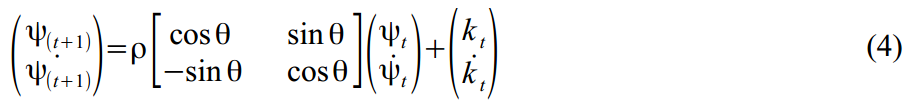
どこで
そして最後に、周期s = 7の週次マイクロサイクルも、三角関数の合計に基づいて構築されます。

現在、上記のすべての式を、カルマンフィルターに適したいわゆる構造形式に整理する必要があります。
測定式は、観察するデータを示しています。

および遷移方程式-構成する変数のダイナミクスを説明します

私たちの場合、方程式(2)-(6)で定義された10の潜在変数があります。
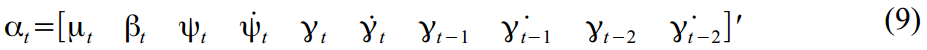
次に、上記のすべての式を行列形式に変換します。
(7)の遷移行列:
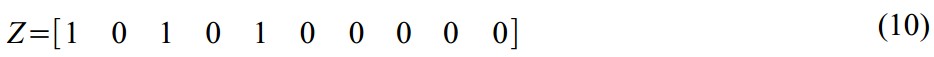
(8)の潜在変数のダイナミクスのこのような弱いマトリックス:
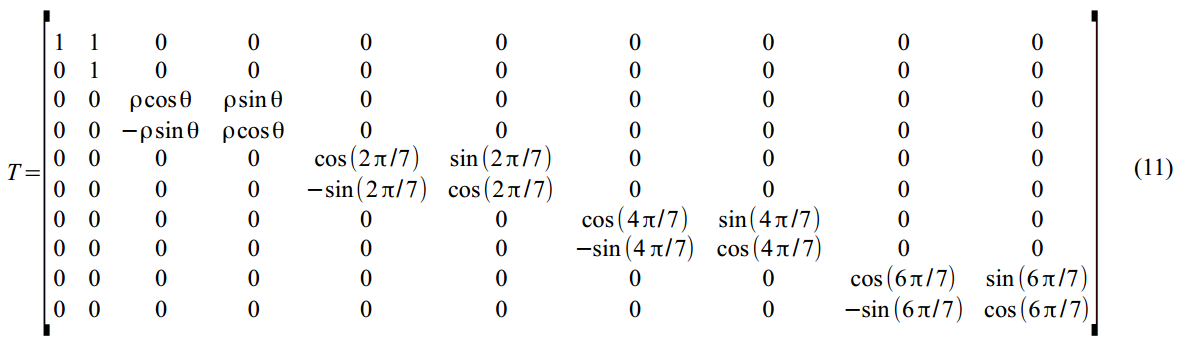
すべての状態のすべてのエラーのベクトル(2)-(6):

行列を使用してダイナミクスの方程式(8)に組み込まれています
そして最後に、(8)のすべてのエラーと摂動のバリエーションのマトリックス:

3.フィルターとカルマンスムーザー
さて、これでカルマンを吸う準備ができました。 変数指定の
初期値を仮定する

どこで
状態ベクトルの計算に加えて、エラーの変動、サイクル周波数、サイクル減衰パラメーターなどの個々のモデルパラメーターを見つけることにも関心があります。 目的のパラメーターのベクトルを次のように呼び出します
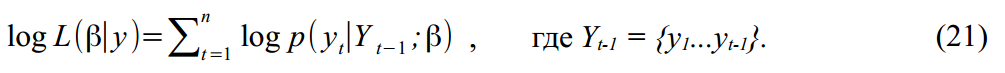
以来
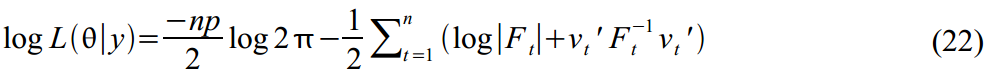
この関数を最大化することにより、必要なパラメーターの推定値を見つけることができます
さて、もう一つのwunderwaffeについてのいくつかの言葉-Kalman smoother(Kalman smoother)、[Durbin、J. and Koopman、2003]、これはまだHabréで言及されていないようです。 一般に、考え方は似ており、カルマンフィルターのみが後続の各値を計算します
カルマン平滑化は逆再帰です。

は、平滑化された状態値のベクトルです
一般的に、理論については長い間書くことができますが、テストするには手がかゆくなります。 それでは、実証的な唯物論に移りましょう。
4.回帰
私はMatlabaの以下のプログラムの最適性と速度のふりをしません。私は本当の溶接工ではありません。すべてのコードは自分のために書かれました。 審美的ではないが、安価で信頼性が高く実用的。 また、フィルターおよびスムージングのコードは、さまざまな初期化オプションなどのために記述されているため、いくぶん冗長です。 コードの一部を捨てようとすると、マトリックスとループでMatlabがクラッシュすることが避けられなかったため、すべてをそのままにしておくことにしました。
すべてが次のように機能します。
- メインプログラムotgr_ssm.mはデータをダウンロードし、 ssmopt構造を準備します。 この構造には、コード内のさまざまな場所に送信される多くの貴重なメモと重要な変数が書き込まれます。 出荷の最後の70の値(10週間)は、予測との比較のために確保されます。予測は、最後に必ず作成されます。
- データは対数尤度関数最大化ルーチンにアップロードされます。 後者の手順は計量経済学でよく使用されるため、メインコードを散らかさないように、別の関数mle_my.mによって一般的な形式ですばやく膝の上に書かれました。
- 求められるパラメーターには状態の分散が含まれるため、それらは厳密に正でなければならず、数値最適化中に常に取得されるとは限りません。 したがって、ポーンをメガネに変更すると、すべての入力分散値は次のように変換されます
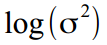 、および減衰係数は範囲で正規化されます
、および減衰係数は範囲で正規化されます 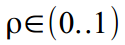 どうやって
どうやって 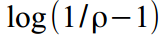 。 さて、出力では、それらは適切な値に変換されます-
。 さて、出力では、それらは適切な値に変換されます- 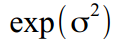 バリエーションと
バリエーションと  減衰係数用。 値ssmopt.transは、変換する必要があるか(1)しないか(0)、どの方向(「in」または「out」)を示すかを示します。 これはすべて、別のtransform.m関数で発生します
減衰係数用。 値ssmopt.transは、変換する必要があるか(1)しないか(0)、どの方向(「in」または「out」)を示すかを示します。 これはすべて、別のtransform.m関数で発生します - mle_my.mは、 kfmy2.mを使用してカルマンフィルター(15)-(22)を実行するオブジェクト関数f_obj.mを呼び出し、対数尤度関数(22)の値を計算し、2回起きないようにカルマンスムーザー(23 )-(27) ksmy2.mを使用します 。 これはすべてmle_my.mに戻り 、関数の最大値(22)に達したかどうかをチェックします。 ある場合は、すべて手順5に進みます。ない場合は、手順2〜4を繰り返します。
最初のフィルターの実行は、次の仮定から始まります。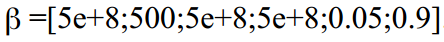 。 多くの変数があるので、ここで試してみてください。6次元関数のグローバルな最大値を探しているため、多くの局所的な極値が可能です。 良い方法では、対数関数の可能な値のグラフを作成し、可能な極値を見ることができます。
。 多くの変数があるので、ここで試してみてください。6次元関数のグローバルな最大値を探しているため、多くの局所的な極値が可能です。 良い方法では、対数関数の可能な値のグラフを作成し、可能な極値を見ることができます。 - 結果-見つかったパラメーターとグラフを表示します。 同時に、70日間の予測を計算し、 frcst.mを使用して実際のデータと比較します
実際には、コード:
otgr_ssm.m
clear all; clc; close all; format long; %------------------- 1. Load and prepare data ------------------------------ load otgruzka.mat; % Structure ssmopt contains several important records used throughout the code ssmopt.frcst=70; % forecast length yend=y(end-ssmopt.frcst+1:end); % saved last observation for the forecast comparison y=y(1:end-ssmopt.frcst); ssmopt.N=length(y); ssmopt.trans=1; % transform estimated parameters to preserve positiveness of variances ssmopt.sv=[5e+8;500;5e+8;5e+8;0.05;0.9]; % starting values ssmopt.mle='f_obj'; % name of the objective function for the maximization ssmopt.sv=transform(ssmopt.sv,'in',ssmopt); ssmopt.filter='kfmy2'; % name of the function computing Kalman Filter ssmopt.smooth='ksmy2'; % name of the function computing Kalman Smoother %------------------- 2. Estimate the model ------------------------------ result=mle_my(y,ssmopt); % call Maximum Likelihood maximization function b=transform(result.b,'out',ssmopt); % transform parameters back % recompute data based on the correct non-transformed parameters ssmopt.trans=0; ssmopt.sv=b; [LH,KF_out,Ksm_out] = feval(ssmopt.mle,b,y, ssmopt); % Recover filtered states series - trend, cycle, and seasonal a_trend=KF_out.Afilt(1,:); a_cycle=KF_out.Afilt(3,:); a_seas=KF_out.Afilt(5,:)+KF_out.Afilt(7,:)+KF_out.Afilt(9,:); y_filt=a_trend+a_cycle+a_seas; % build the estimated filtered series Y % Recover smoothed states series - trend, cycle, and seasonal a_trendsm=Ksm_out.Asm(1,:); a_cyclesm=Ksm_out.Asm(3,:); a_seassm=Ksm_out.Asm(5,:)+Ksm_out.Asm(7,:)+Ksm_out.Asm(9,:); y_smooth=a_trendsm+a_cyclesm+a_seassm; % build the estimated smoothed series Y result=mle_my(y,ssmopt); % find correct Hessian for non-transformed parameters %------------------- 3. Compute estimation statistics ------------------------------ %Find standard errors, and p-values se=sqrt(abs(diag(inv(result.hessian)/ssmopt.N))); % se(b) tstat=b./se; % t-statistics pval=2*(1-tcdf(abs(tstat),ssmopt.N-length(ssmopt.sv))); % p-value % Display output fprintf('Estimated parameters and p-values:\n'); out=[b pval] period=2*pi/b(end-1) % Compute R-squared resid=y-y_filt; % estimation errors SSE=resid*resid'; % Sum of Squared Errors SST=(y-mean(y))*(y-mean(y))'; % Sum of Squares Total R2=1-SSE/SST % R-squared' %------------------- 4. Make Forecast ------------------------------ af0=KF_out.Afilt(:,end-ssmopt.frcst); [yf,af]=frcst(b,y,ssmopt, af0); %------------------- 5. Plot results ------------------------------ %p=ssmopt.N; p=600; t=[1:1:p]; figure(1) plot(t,y(1:p),'k',t,y_filt(1:p),'b',t,y_smooth(1:p),'r--') title('Original, Filtered, and Smoothed data') legend('y(t)','y filtered','y smoothed'); figure(2) plot(t,y(1:p),'k',t,a_trend(1:p),'b',t,a_trendsm(1:p),'r--') title('Original data, Filtered and Smoothed trend') legend('y(t)','Filtered trend','Smoothed trend'); figure(3) plot(t,a_cycle(1:p),'b',t,a_cyclesm(1:p),'r--') title('Filtered and Smoothed cycle') legend('Filtered cycle','Smoothed cycle'); figure(4) % Filtered + smoothed seasonal plot(t,a_seas(1:p),'b',t,a_seassm(1:p),'r--') title('Filtered and Smoothed weekly seasonal') legend('Filtered seasonal','Smoothed seasonal'); t=[1:1:ssmopt.frcst]; figure(5) plot(t,yend,'b',t,yf,'r--') title('Original data and Forecast') legend('Original data','Forecast'); RMSE=sqrt(sum((yend - yf).^2)/ssmopt.frcst) % Root Mean Squared Error
mle_my.m
function result_mle=mle_my(y,mleopt); warning off; %---------------- 1. Set-up minimization options ---------------- options=optimset('fminunc'); options=optimset('LargeScale', 'off' , ... 'HessUpdate', 'bfgs' , ... 'LineSearchType', 'quadcubic' , ... 'GradObj' , 'off' , ... 'Display','off' , ... 'MaxIter' , 1000 , ... 'TolX', 1e-12 , ... 'TolFun' , 1e-12, ... 'DerivativeCheck' , 'off' , ... 'Diagnostics' , 'off' , ... 'MaxFunEvals', 1000); %---------------- 2. Run minimization ---------------- [b,fval,exitflag,output,grad,hessian]=fminunc(mleopt.mle,mleopt.sv,options,y,mleopt); warning on; result_mle.b=b; result_mle.fval=fval; result_mle.output=output; result_mle.hessian=hessian;
f_obj.m
function [obj,KF_out,Ksm_out]=f_obj_tr(b,y,ssmopt); %---------------- 1. Recover parameters ------------------------------------ b=transform(b,'out',ssmopt); s2_irr=b(1); s2_tr=b(2); s2_cyc=b(3); s2_seas=b(4); freq=b(5); rho=b(6); %---------------- 2. Build the model ------------------------------------ ssmopt.ssmodel.states=10; ssmopt.ssmodel.Z=[1 0 1 0 1 0 1 0 1 0]; T1 = [1 1 0 0; 0 1 0 0; 0 0 rho*cos(freq) rho*sin(freq); 0 0 -rho*sin(freq) rho*cos(freq)]; T2=[cos(2*pi/7) sin(2*pi/7) 0 0 0 0;... -sin(2*pi/7) cos(2*pi/7) 0 0 0 0;... 0 0 cos(4*pi/7) sin(4*pi/7) 0 0;... 0 0 -sin(4*pi/7) cos(4*pi/7) 0 0;... 0 0 0 0 cos(6*pi/7) sin(6*pi/7);... 0 0 0 0 -sin(6*pi/7) cos(6*pi/7)]; ssmopt.ssmodel.T = [T1 zeros(rows(T1),cols(T2));zeros(rows(T2),cols(T1)) T2]; ssmopt.ssmodel.R=eye(10); ssmopt.ssmodel.R(1,1)=0; H=s2_irr; Q=zeros(10,10); Q(2,2)=s2_tr; Q(3,3)=s2_cyc; Q(4,4)=s2_cyc; Q(5,5)=s2_seas; Q(6,6)=s2_seas; Q(7,7)=s2_seas; Q(8,8)=s2_seas; Q(9,9)=s2_seas; Q(10,10)=s2_seas; %---------------- 3. Suggest starting conditions for the states ------------------------ a0=[y(1);0;0;0;0;0;0;0;0;0]; P0=eye(ssmopt.ssmodel.states)*1e+10; %---------------- 4. Run Kalman filter ------------------------ KF_out = feval(ssmopt.filter,y, ssmopt, Q, H, a0, P0); obj=KF_out.LH; %---------------- 5. Run Kalman smoother ------------------------ if nargout>2 ssmopt.ssmodel.num_etas=3; % number of the state variances (required for Kalman smoother) Ksm_out = feval(ssmopt.smooth,KF_out, ssmopt); end
kfmy2.m
% Kalman filter % y[t] = Z*alpha[t] + eps, eps ~ N(0,H). % alpha[t] = T*alpha[t-1] + R*eta, eta ~ N(0,Q). % v[t]=y[t]-E(y[t]) = y[t]-Z*a[t] % F[t]=var(v[t]) function KF_out = kfmy_koop(y, ssmopt, Q, H, a, P); N=ssmopt.N; m=ssmopt.ssmodel.states; %---------------- 1. Recover parameters and prepare matrices ---------------- T=ssmopt.ssmodel.T; Z=ssmopt.ssmodel.Z; R=ssmopt.ssmodel.R; KF_out.Vmat=zeros(1,N); KF_out.Fmat=zeros(1,N); KF_out.Afilt=zeros(m,N); KF_out.Pfilt=zeros(m,m,N); KF_out.Kmat=zeros(m,N); KF_out.Lmat=zeros(m,m,N); LHmat=zeros(1,N); if ~isfield(ssmopt,'exactcheck'); ssmopt.exactcheck=1; % set exact filter initialization by default end; %---------------- 2. Set default starting values for a and P , if none provided ---------------- Pinf=eye(m); if nargin < 6 if ssmopt.exactcheck==1 P=zeros(m,m); else P=eye(m)*1000000000; end end if nargin < 5 a=[y(1); zeros(m-1,1)]; end KF_out.Afilt(:,1)= a; KF_out.Pfilt(:,:,1) = P; d=0; %---------------- 3. Exact Filtering ---------------- if ssmopt.exactcheck==1 evals=10; % number of time steps to evaluate until Pinf converges to zero KF_out.exact.F1=zeros(1,evals); KF_out.exact.F2=zeros(1,evals); KF_out.exact.L1=zeros(m,m,evals); KF_out.exact.Pinf=zeros(m,m,evals); KF_out.exact.Pinf(:,:,1)=Pinf; for i=1:evals if sum(sum(Pinf))<1e-20; d=i-1; % time point after which Pinf-->0, and after which we may start regular Kalman filter break; else if sum(Pinf*Z')>0 % Pinf is not singular F1=inv(Z*Pinf*Z'); F2=-F1*(Z*P*Z'+H)*F1; K=T*Pinf*Z'*F1; K1=T*(P*Z'*F1+Pinf*Z'*F2); L=TK*Z; L1=-K1*Z; P=T*Pinf*L1' + T*P*L' + R*Q*R'; Pinf=T*Pinf*L'; else F1=Z*P*Z'+H; F2=F1; K=T*P*Z'/F1; L=TK*Z; L1=L; P=T*P*L' + R*Q*R'; Pinf=T*Pinf*T'; end v=y(i) - Z*a; a=T*a+K*v; %save filtered estimates KF_out.Afilt(:,i+1)=a; KF_out.Pfilt(:,:,i+1)=P; KF_out.Vmat(i)=v; KF_out.Fmat(i)=F1; KF_out.Kmat(:,i)=K; KF_out.Lmat(:,:,i)=L; LHmat(i) = -0.5*(log(2*pi*F1) + v^2/F1); %save exact values for smoother KF_out.exact.F1(i)=F1; KF_out.exact.F2(i)=F2; KF_out.exact.L1(:,:,i)=L1; KF_out.exact.Pinf(:,:,i+1)=Pinf; end end end %---------------- 4. Regular Filtering ---------------- for i=d+1:N v=y(i) - Z*a; f=Z*P*Z' + H; K=T*P*Z'/f; L=TK*Z; a=T*a+K*v; P=T*P*L'+R*Q*R'; if i<N KF_out.Afilt(:,i+1)=a; KF_out.Pfilt(:,:,i+1)=P; end KF_out.Vmat(i)=v; KF_out.Fmat(i)=f; KF_out.Kmat(:,i)=K; KF_out.Lmat(:,:,i)=L; LHmat(i) = -0.5*(log(2*pi*f) + v^2/f); end %---------------- 5. Prepare output ---------------- KF_out.LH=-sum(LHmat); KF_out.Q=Q; KF_out.H=H; KF_out.exact.d=d; end
ksmy2.m
function [Ksm_out, Kdism_out] = ksmy2(KF_out, ssmopt); [m,N]=size(KF_out.Afilt); meta=ssmopt.ssmodel.num_etas; %---------------- 1. Recover filtered matrices ---------------- Fmat=KF_out.Fmat; Vmat=KF_out.Vmat; Pfilt=KF_out.Pfilt; Afilt=KF_out.Afilt; Q=KF_out.Q; H=KF_out.H; %---------------- 2. Recover Model structure ---------------- Z=ssmopt.ssmodel.Z; T=ssmopt.ssmodel.T; R=ssmopt.ssmodel.R; Asm=zeros(m,N); Psm=zeros(m,m,N); rmat=zeros(m,N); Nmat=zeros(m,m,N); Eps=zeros(1,N); Eta=zeros(meta,N); Kmat=KF_out.Kmat; Lmat=KF_out.Lmat; if ~isfield(KF_out,'exact'); KF_out.exact.d=0; end d=KF_out.exact.d; if KF_out.exact.d>0 L1=KF_out.exact.L1; F1=KF_out.exact.F1; F2=KF_out.exact.F2; Pinf=KF_out.exact.Pinf; end %---------------- 3. Regular Smoothing for t=N..d+1 observations ---------------- for i=N:-1:d+1 r=Z'/Fmat(i)*Vmat(i) + Lmat(:,:,i)'*rmat(:,i); N=Z'/Fmat(i)*Z + Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); Asm(:,i)=Afilt(:,i) + Pfilt(:,:,i)*r; Psm(:,:,i)=Pfilt(:,:,i)-Pfilt(:,:,i)*N*Pfilt(:,:,i); if i>1 rmat(:,i-1)=r; Nmat(:,:,i-1)=N; end if nargout>1 Eps(i)=H*(1/(Fmat(i))*Vmat(i)-Kmat(:,i)'*rmat(:,i)); Eta(:,i)=Q*R'*rmat(:,i); end end %---------------- 4. Exact Smoothing for t=d..1 observations ---------------- if KF_out.exact.d>0 r1=zeros(m,1); N1=zeros(m,m); N2=zeros(m,m); for i=d:-1:1 if sum(Pinf(:,:,i)*Z')>0 %cond(Pinf)<1e+12 % Pinf is not singular r1=Z'*F1(i)*Vmat(i) + Lmat(:,:,i)'*r1 + L1(:,:,i)'*rmat(:,i); N2=Z'*F2(i)*Z + Lmat(:,:,i)'*N2*Lmat(:,:,i) + Lmat(:,:,i)'*N1*L1(:,:,i) + L1(:,:,i)'*N1*Lmat(:,:,i) + L1(:,:,i)'*Nmat(:,:,i)*L1(:,:,i); N1=Z'*F1(i)*Z + Lmat(:,:,i)'*N1*Lmat(:,:,i) + L1(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); r=Lmat(:,:,i)'*r1; N=Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); if nargout>1 Eps(i)=-H*Kmat(:,i)'*rmat(:,i); Eta(:,i)=Q*R'*rmat(:,i); end else % Pinf is singular r1=T'*rmat(:,i); N2=T'*N2*T; N1=T'*N1*Lmat(:,:,i); r=Z'/(Fmat(i))*Vmat(i) + Lmat(:,:,i)'*rmat(:,i); N=Z'/(Fmat(i))*Z + Lmat(:,:,i)'*Nmat(:,:,i)*Lmat(:,:,i); if nargout>1 Eps(i)=H*(1/Fmat(i)*Vmat(i) - Kmat(:,i)'*rmat(:,i)); Eta(:,i)=Q*R'*rmat(:,i); end end if i>1 rmat(:,i-1)=r; Nmat(:,:,i-1)=N; end Asm(:,i)=Afilt(:,i) + Pfilt(:,:,i)*r + Pinf(:,:,i)*r1; Psm(:,:,i)=Pfilt(:,:,i)-Pfilt(:,:,i)*N*Pfilt(:,:,i) - (Pinf(:,:,i)*N1*Pfilt(:,:,i))' - Pinf(:,:,i)*N1*Pfilt(:,:,i) - Pinf(:,:,i)*N2*Pinf(:,:,i); end end %---------------- 5. Prepare output ---------------- Ksm_out.Asm=Asm; Ksm_out.Psm=Psm; Ksm_out.Kmat=Kmat; Ksm_out.Lmat=Lmat; Ksm_out.Nmat=Nmat; Ksm_out.rmat=rmat; Kdism_out.Eps=Eps; Kdism_out.Eta=Eta;
transform.m
function b=transform(b,howto,ssmopt); k=length(b); if strcmp(howto,'in') % in-transformation if ssmopt.trans==0 % no transformation b=b; end; if ssmopt.trans==1 % transformation to preserve the positiveness of variances b(1:k-1,:)=log(b(1:k-1,:)); b(k)=log(1/b(k)-1); end; else % out-transformation if ssmopt.trans==0 % no transformation b=b; end; if ssmopt.trans==1 b(1:k-1,:)=exp(b(1:k-1,:)); b(k)=1/(1+exp(b(k))); end; end
5.結果
(見つかった評価のp値は括弧内に示されています)
| 観測された系列の誤差の分散 | 1.77E + 009(0.00) |
| トレンドエラー分散 | 348.73(0.00) |
| サイクル分散 | 6.07E + 008(0.00) |
| 季節成分誤差の分散 | 3.91E + 006(0.00) |
| サイクル頻度 | 3.91E + 006(0.00) |
| サイクル期間(日数) | 362.6(0.00) |
| ループ減衰係数 | 0.891(0.00) |
| R二乗回帰 | 0.78 |
6.チャート
わかりやすくするため、グラフは最初の600日間のみ表示され、シリーズ全体ではネタバレの下に隠れています。
a。 生、フィルター、および平滑化されたデータ
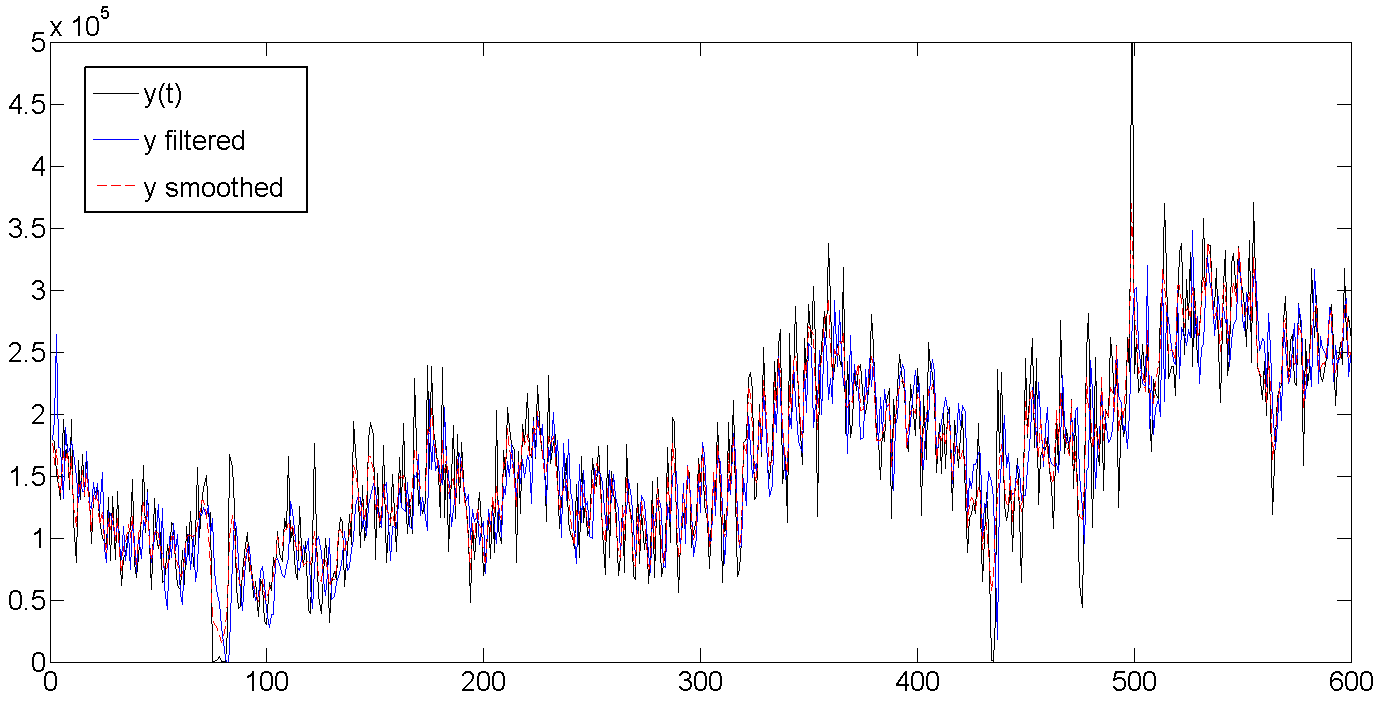
行全体 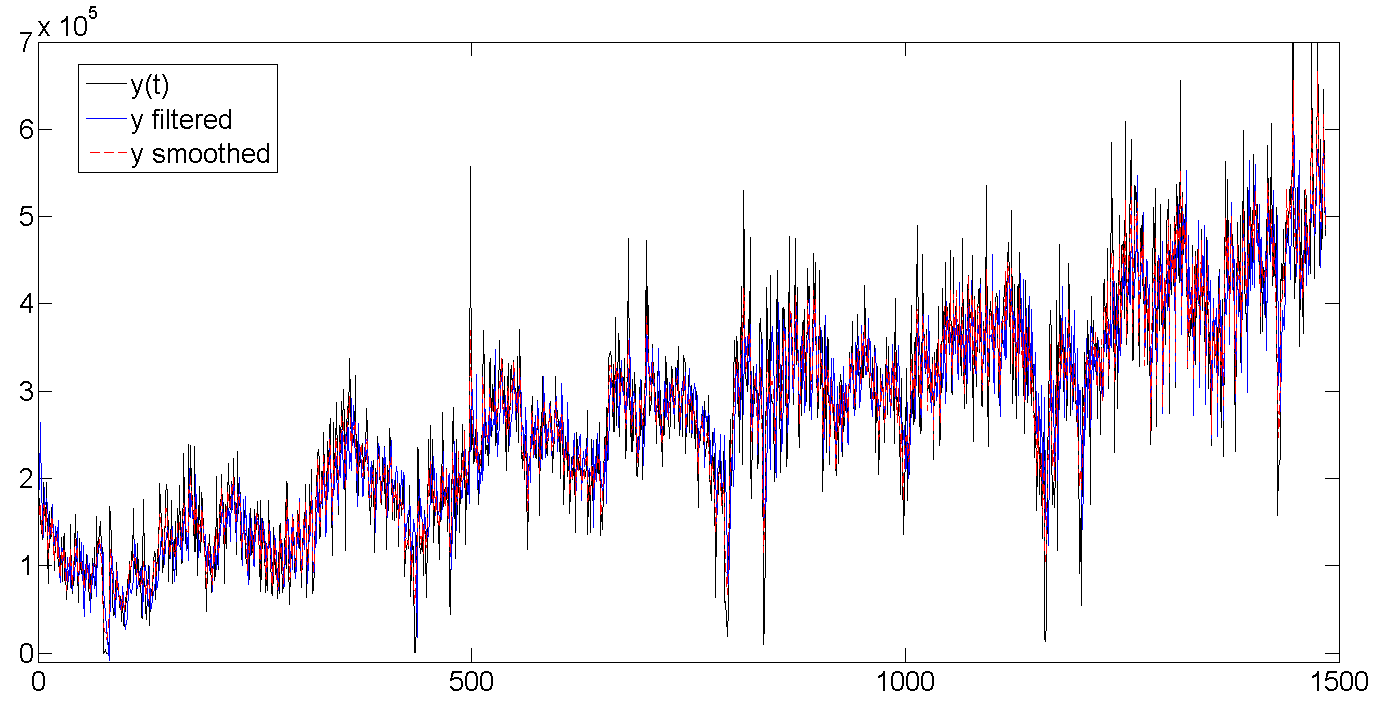

b。 ソースデータ、フィルター処理された傾向、平滑化された傾向
ご覧のように、カルマンフィルターは以前の値に基づいて傾向を推測しようとしているため、関係者のラインに合わせて変動しますが、データがさらに進む場所を推測しようとして少し遅れます。 Kalmanはシリーズ全体をよりスムーズに「見る」ため、トレンドはより滑らかで落ち着いたように見えます。

行全体 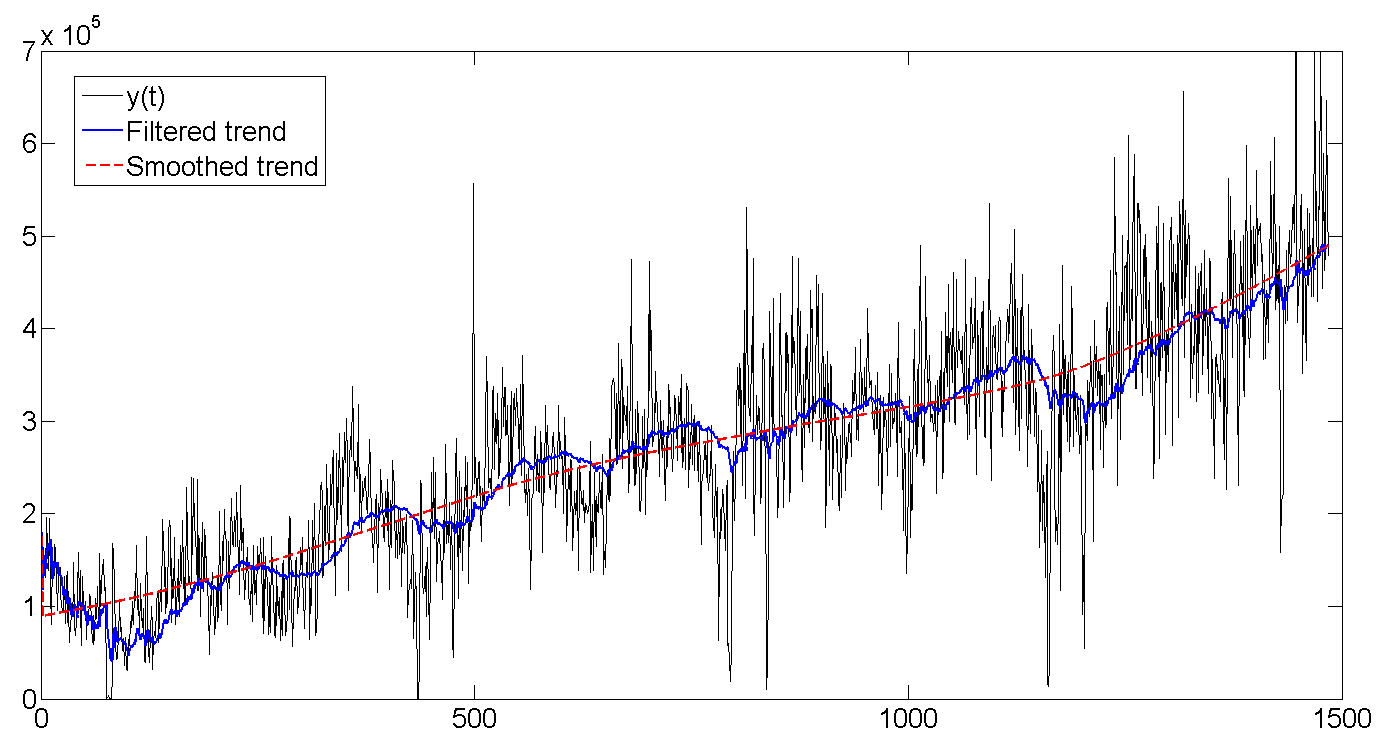

c。 フィルター処理および平滑化されたループ
結果の表からわかるように、平均サイクルの長さは約362日、またはほぼ1年です(だれが驚くでしょう)。 また、潜在変数の初期値をゼロに設定し、1e + 10のオーダーの非常に大きな分散を設定するため、フィルターが最初にどのように調整を開始し、データを完全に失うかを見ることができます。 ただし、通常、フィルターをリズムに合わせるには、最初の数回の試行で十分です。 ところで、この作業では、フィルターの正確な初期化(正確な初期化)を使用しました。これにより、フィルター処理された値がデータをすばやく取得できるようになります。

行全体 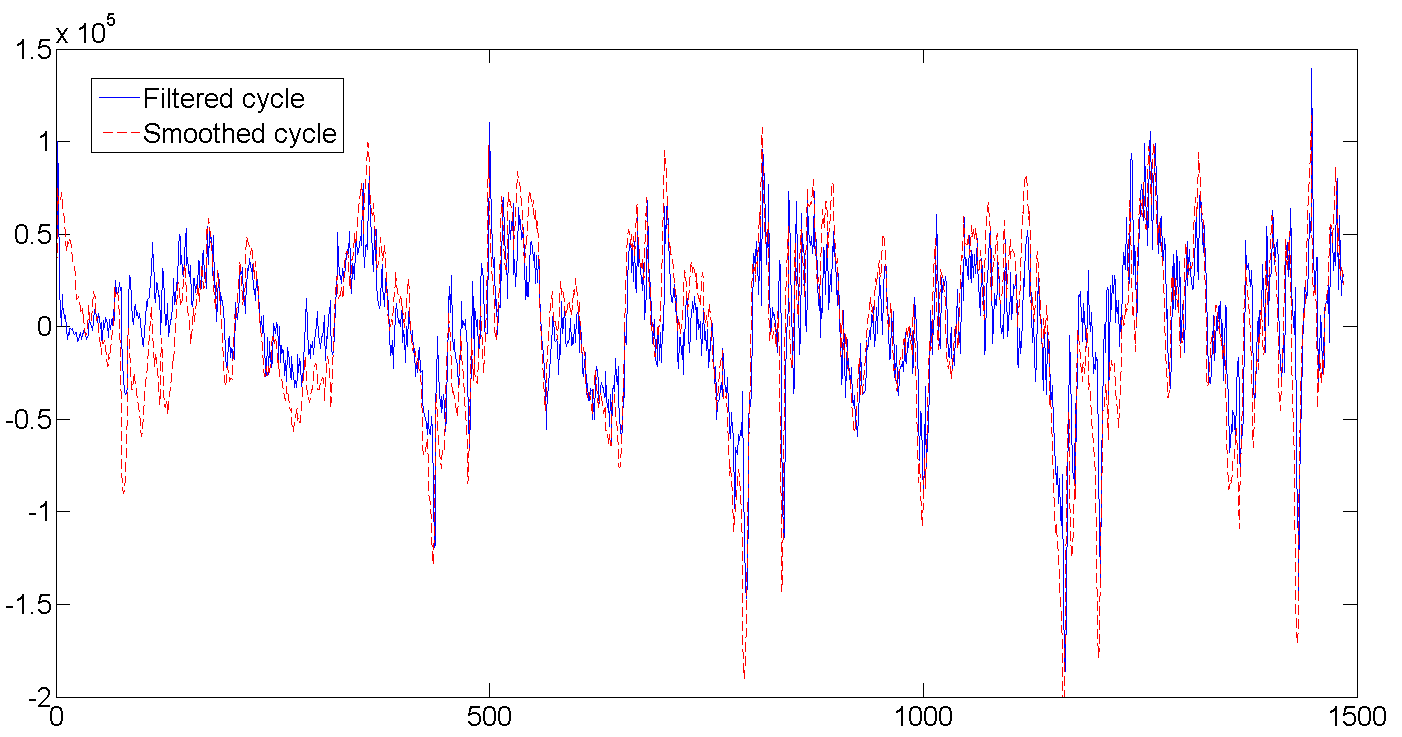

d。 フィルター処理および平滑化された毎週の季節要因
出荷数は徐々に増加しており、毎日のボラティリティは増加しています。
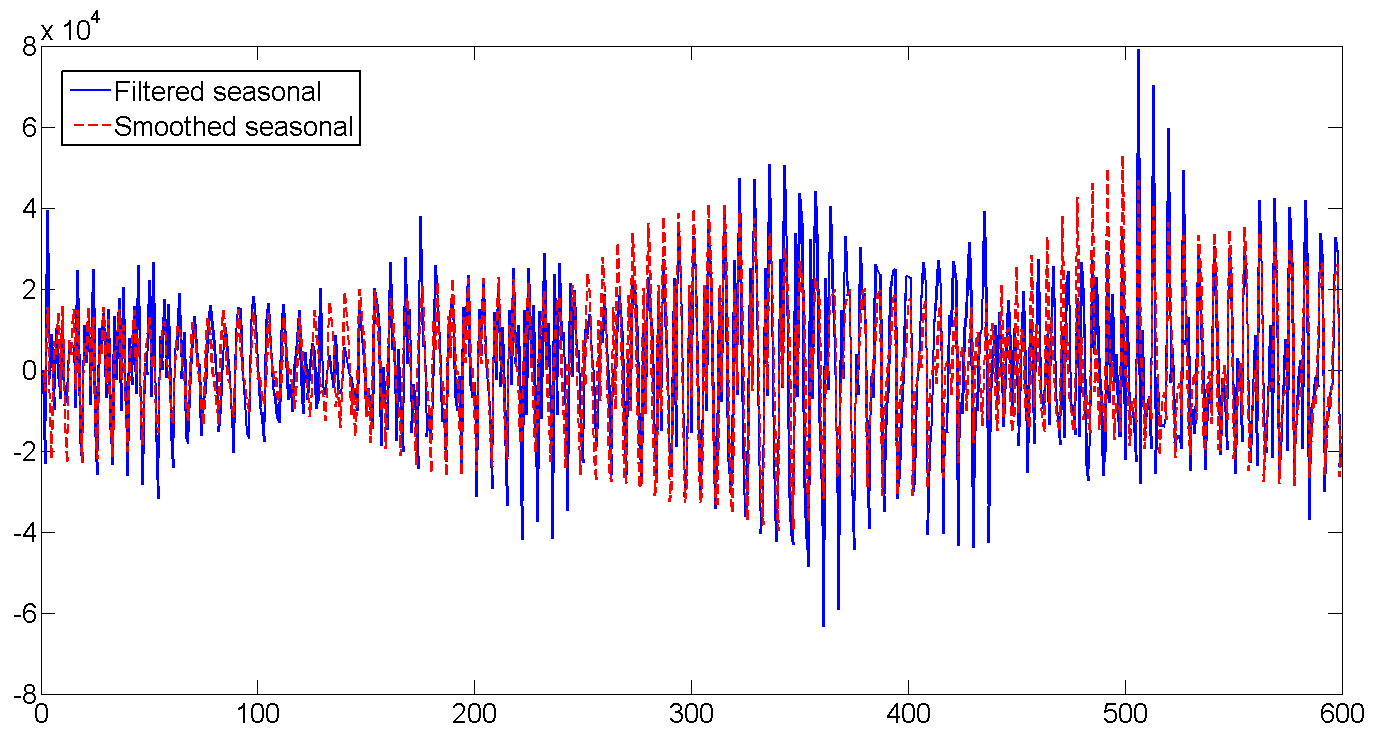
行全体 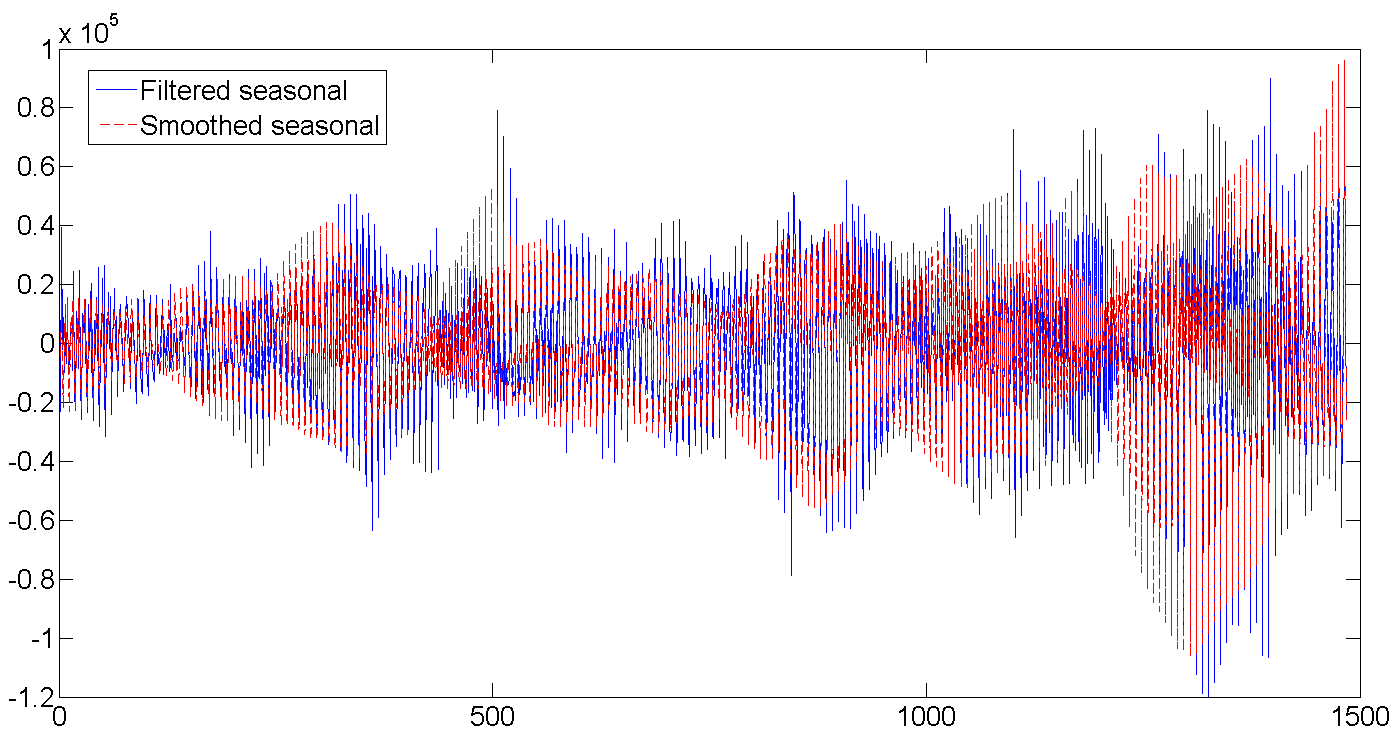

6.予測
取得したパラメーターに基づいて、フィルター処理された状態の最新の値を使用して、70日間(10週間)の予測を作成し、既存のデータと比較します。 一般的に、予測は見栄えがよく、それが生命を与えるフィルターの役割です。 曜日ごとのボラティリティの推測は特に喜ばしいことです。 構築された予測の全体の長さをよく見て、想像力を有効にすると、年間出荷サイクルの下で予測がどのように曲がるかを見ることができます。 予測が機能しなかった唯一の瞬間は26〜32日です。 しかし、明らかに出荷がほぼ毎週低下し、その後すぐに急激なジャンプが発生しました。このようなケースはシリーズの最初に一度しか発生しなかったため、予測することはほとんど不可能でした。 一般的に、落ちたのは曇りからです。
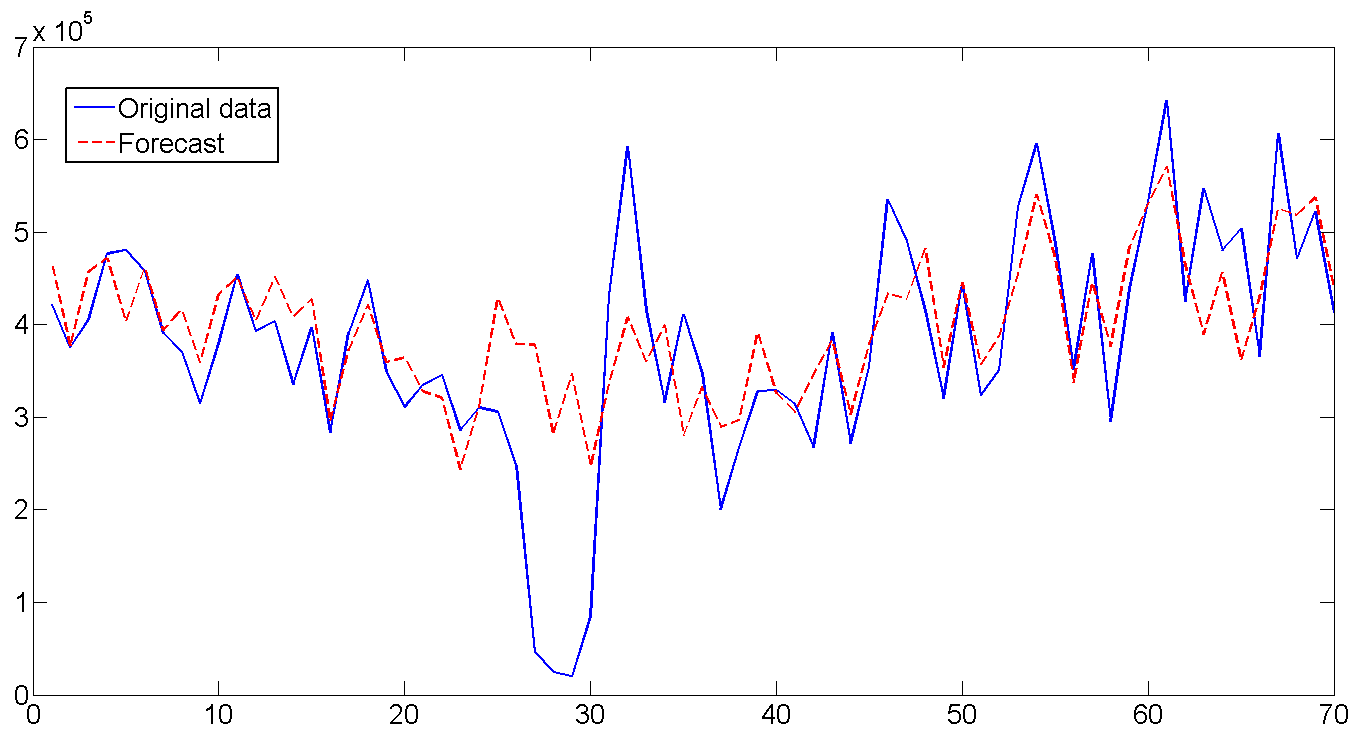
モデルを比較する場合、予測RMSEは1.112e + 005です。
まあ、それだけです。
ご注意
状態空間モデルは、計量経済学において価値のあるものと見なされるべきではありません。 それどころか、それらはより多くの特定のモデルの一般化されたバージョンを表します。 たとえば、MA(1)プロセス

SSM形式で簡単に想像できます。
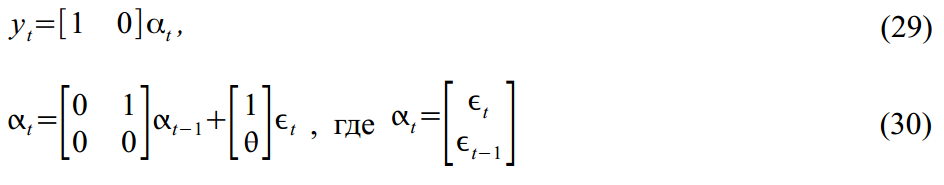
またはARMA(2,1)プロセス:
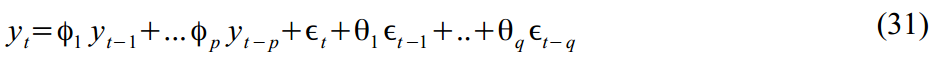
SSM形式でパック:
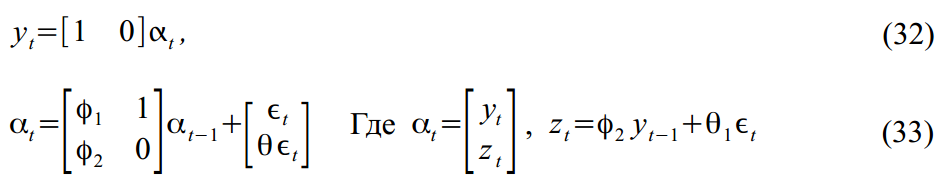

SSM形式で簡単に想像できます。
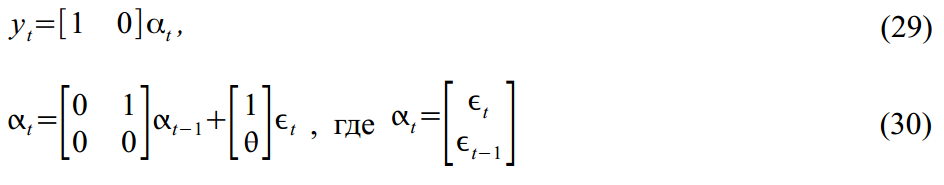
またはARMA(2,1)プロセス:
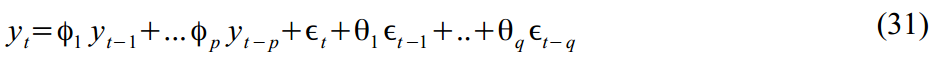
SSM形式でパック:
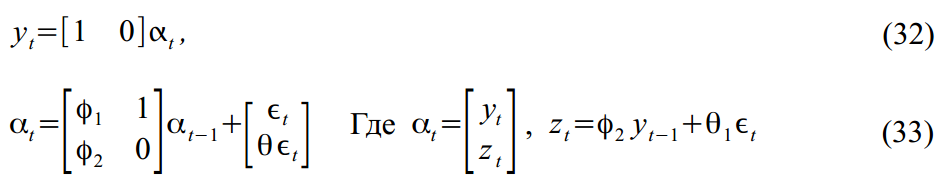
関連文献
- Durbin、J。、およびKoopman、状態空間法によるSJ時系列分析。 オックスフォード:オックスフォード大学出版局、2001。
- Durbin、J。、およびKoopman、SJ「状態空間時系列分析のためのよりシンプルで効率的なシミュレーション」Biometrika vol。 89、第3号、2002年。
- Harvey、AC、およびJaeger、A。「トレンド除去、定型化された事実およびビジネスサイクル。」Journal of Applied Econometrics(8)、1993。
- Harvey、AC「予測、構造時系列モデル、およびカルマンフィルター」 ケンブリッジ:ケンブリッジ大学出版局、1989年。