この記事を理解するには、高校の9年生レベルで最低限のプログラミングスキルと数学の知識が必要です。 この記事は、最適化方法に精通していないか、この方向で最初の一歩を踏み出しただけの人を対象としています。
読者を最大限に活用するために、私は正式な定義をほぼ完全に放棄し、完全に正確でない単純化を意識的に行わなければなりませんでした。 私は子供を水で捨てないことを願っています（もしこれが起こったら、私はあなたから聞いてうれしいです）。
最適化について
最適化とは何かを理解するには、まずそれが何のためにあるのかを知る必要があります。 このレポートで自分自身に気付かないうちに、私たちは日常生活の中で「最適化タスク」とうらやましい規則性に直面しているとすぐに言わなければなりません。
別の給料を受け取った私たちが家計をノックアウトすると決めたと仮定します。 まず、最も重要なニーズ（食料、電気料金、インターネットなど）を満たすようにお金を分配する必要があり、バランスをより低い優先度に下げることができます。 すべてのお金でデザイナーの携帯電話を購入し、飢え死にすることは最良の解決策ではありません、あなたはそれを見つけることができますか？
または別のオプションとして、キャンプに行ってランドセルを集めることにしました。 一つの問題-たくさんのものがあり、私たちのかばんは大きすぎません（そして私たち自身は限られた収容力を持っています）。 私たちは、私たちにとって最も重要なアイテムをできるだけ多く取りたいと思っています。 山に行く場合、私たちと一緒に安全ロープをつかむのは良い決断であり、代わりに私たちのお気に入りのPlayStation Vitaを取り、残りをクッキーで満たすことはおそらくあまり良くありません。
それで、最適化は何をしますか？ 彼女は同じ、良い解決策を探しています。 おそらくすべてのベストではありませんが、間違いなく良いです。
少しフォーマルになりました。 ウィキペディアを見ると、この定義を簡単に見つけることができます。
最適な（lat。Optimusから-最高の）ソリューションは、何らかの理由で他よりも望ましいソリューションです。 したがって、最適化は最適なソリューションを見つける方法です。
今、私たちの決定がどれほど良いかを測定できると想像してみましょう。 たとえば、「サッチェル問題」の場合、各物に自然数を割り当てます（数が大きいほど物が重要になります）。 次に、タスクはより明確なステートメントを取得します。ランドセルをそのようなもので満たし、その優先順位の合計は最大になり、重みは特定の値を超えないようにします。 つまり 通常、 ターゲットと呼ばれる関数の最大値を探しています。
すべてを単一の分母に減らすには、再びウィキペディアを見てください。
最適化（数学）-特定の領域における目的関数の極値（最小または最大）を見つけます。
最適化の実行内容について多かれ少なかれ決定したので、「どのように？」という合理的な疑問が生じます。
もちろん、特にすべてのソリューションをわざわざ整理して比較することはできません。 ナップザックの場合、おそらくこれを行うことさえできます。 しかし、今、私たちのかばんがまったくかばんではなく、多くのワゴンを備えた列車全体であり、異なる商品を別の都市に輸送すると想像してみましょう。 タスクは変更されておらず（できるだけ価値のあるものをロードするため）、ターゲット関数は商品の合計値になります。 ソリューションを完全に整理するにはどれくらい時間がかかりますか？ 私はたくさん思います。
ソリューションをランダムに選択できます。 数百のソリューションを考えて、それらからベストを選びましょう。 間違いなく、これは徹底的な検索よりもはるかに高速になりますが、最終的なソリューションが極値に近づくことを誰が保証しますか？
私は苦しみませんし、非常に多くの最適化方法があると言います 。 それらをクラスに分割するのが習慣であるため、すべてをリストするわけではありません。 「シミュレーテッドアニーリング」とは、確率論的手法（ギリシャ語から。Στοχαστικός-「 推測 」）または確率論的手法のことを指しているとしか言えません。 そして、確率はどこにあり、解決策を見つけるのにどのように役立つか-少し低いです。
シミュレーテッドアニーリング
すべての独創的なのと同様に、この方法は母なる自然によって見張られています。 物質の結晶化のプロセスは、金属の均一性を高めるためにunningの冶金師によって順応された基礎として採用されています。
各金属には結晶格子があり、非常に簡単に言えば、物質の原子の幾何学的位置を表します。 すべての原子の位置のセットはシステムの状態と呼ばれ、各状態は特定のレベルのエネルギーに対応します。 アニーリングの目的は、システムを最小のエネルギー状態にすることです。 エネルギーレベルが低いほど、結晶格子は「より良く」なります。 彼女が持っている欠陥が少なくなり、金属が強くなります。
アニーリング中、金属はまず特定の温度に加熱され、結晶格子の原子がその位置を離れます。 その後、ゆっくりと制御された冷却を開始します。 原子はエネルギーの少ない状態になる傾向がありますが、一定の確率で原子はより多くの状態になります。 この確率は温度とともに減少します。 最悪の状態への移行は、奇妙なことに、最初の状態よりもエネルギーが少ない状態を最終的に見つけるのに役立ちます。 温度が所定の値まで低下すると、プロセスは終了します。
ご覧のとおり、このプロセスのフレームワークでは、エネルギーが最小限に抑えられます。 エネルギーを目的の機能に変えてしまいます。 かどうか？ なぜこのようなトリッキーなプロセスがこれほど優れているのか、考えてみましょう。 たとえば、なぜ私たちは常にエネルギーの少ない州に行かないのですか？
これは、広く使用されている勾配降下法の仕組みです。
インターネット上で、アルゴリズムのすべての利点を可能な限り最良の方法で示す完全に素晴らしい画像を見つけることができました。
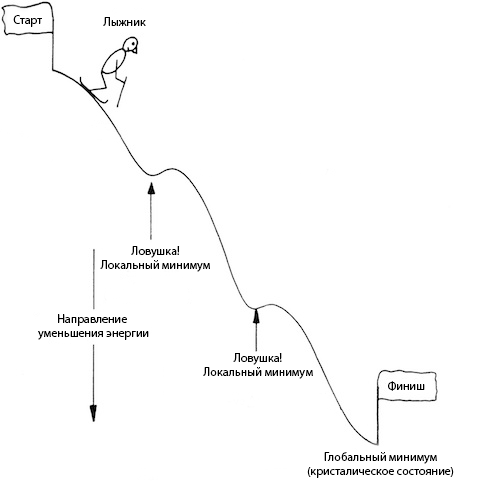
スキーヤーがターゲット関数の急な斜面に沿って急いでいると想像してみましょう。 タスクは、最も低いポイント（グローバルな最小値）まで下げることです。 しかし、あなたが見るように、私たちが出会った斜面は完全に平坦ではなく、そこに低地があり、そこに追い込まれたので、私たちはすでに足元にいるように思えるかもしれません。 バカにならないように、私たちは好奇心を示し、降下を続けるために小さなマウンドに登らなければなりません。
メタファーを完全に理解できるようにするために、スキーヤーの例では、勾配は物質のエネルギーを測定する関数です（客観関数でもあります）。 よりエネルギーのある状態への確率論的な移行は、低地の右側の丘を登ることです。
ご覧のとおり、このようなアルゴリズムにより、ローカルミニマムで「スタック」を回避する可能性が高くなります。
これで、メソッドのより厳密な説明に進む準備ができました。 次の表記法を紹介します。
Sを問題のすべての状態（解）のセットとします。 たとえば、ランドセルの問題の場合は、あらゆる種類の物事が大量に発生します。
させて
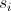-アルゴリズムのi番目のステップの状態。 
。
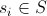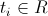-i番目のステップの温度。
シミュレーテッドアニーリングを使用するには、3つの関数を定義する必要があります。
- エネルギーの機能、またはより簡単に言えば、最適化するもの。
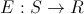
- 時間の経過に伴う温度変化の関数。 念のために、予約数を減らす必要があることを予約します。
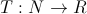
- 新しい状態を生成する関数。
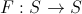
次に、それぞれについて詳しく説明します。
Eは、いくつかの規則に従って、各決定を数値に関連付けます。 特定のタスクに依存します。
Tは、反復回数iを温度に関連付けます。 この関数は、アルゴリズムの動作時間を決定します（実際には、より深い意味を持っていますが、これをまだ知る必要はありません）。 Tが線形関数の場合、実行時間は比較的長くなります。 べき関数の場合、言う
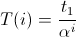、すべてが非常に迅速に終了しますが、低地で立ち往生しないという事実からはほど遠いため、フィニッシュラインに到達しません。
この記事では、最も単純な線形オプションを選択しました。
function [ T ] = DecreaseTemperature( initialTemperature, i) %initialTemperature - %i - T = initialTemperature * 0.1 / i; end
この記事のすべてのコードはMatlabで書かれていることをすぐに言わなければなりません。 この環境を選んだのは、「箱から出して」すぐに美しいグラフィックを描くことができるからです。 コードをお気に入りの言語に簡単に移植できるように、特定のmatlabマジックを使用せずに記述しようとしました。
関数Fは、以前の状態に基づいて、新しい候補状態を生成し、システムはこの状態に移行するか、ドロップすることができます。 聞かせて
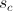。 候補を取得する方法は、解決される問題に完全に依存しており、例で特定の機能を確認できます。
これで、アニーリングシミュレーション法のアルゴリズムを最も一般的な形で説明できます。
- 入口：最低温度
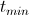初期温度 
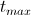
- 任意の最初の状態を設定します
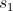
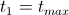
- さようなら
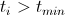
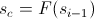
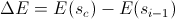
- もし
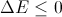それから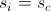 
- もし
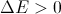遷移は確率で実行されます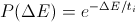 
- 温度を下げる
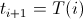
- 最後の状態を返します
ご覧のとおり、すべてが非常に単純であり、新しい状態への移行のみを個別に説明する価値があります。 「候補」のエネルギーが少ない場合、新しい状態になります。そうでない場合、遷移は確率的です（したがって、この方法は確率論として分類されます）。
これが間違いなく困難を引き起こさないように、確率理論の最も基本的な概念のいくつかを思い出すことができます。
非公式には、イベントが発生する可能性の尺度として確率を定義します。 信頼できるイベント（確実に発生するイベント）の確率は、1、つまり不可能、つまりゼロです。 他の値はすべて中間です。
たとえば、サイコロを投げるとき、任意の数から落ちる確率は1で、トリプルは1/6です。
私たちの場合、エネルギー差の値を式に代入します
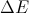と温度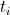 
遷移の確率を取得します。 この移行を実行することだけが残っていますが、どうすればよいですか？
確率計算コード：
function [ P ] = GetTransitionProbability( dE, T ) P = exp(-dE/T); end
単一のセグメントを想像して、確率の値に応じて2つの部分に分割します。
次に、関数を使用して均一に分布した乱数を生成します。Matlabでは（他のほとんどすべての言語と同様に）randです。 次に、この番号をセグメントにマークします。
数値が左側に落ちた場合-右側に移行します-何もしません。
function [ a ] = IsTransition(probability) value = rand(1); if(value <= probability) a = 1; else a = 0; end end
今、私は、すべてが明確であり、最初のタスクの解決策に直接進むことができると思います。
セールスマンの問題
あなたが旅行商人で、国内のすべての都市の住民に商品を提供したいと想像してください。 旅行には多くの時間と労力がかかるので、乗り越えられる距離が最小になるようにルートを作成することは論理的です。 このルートはまだ見つかりません。
より正式には、各都市を通り、出発地で終わる最短経路を見つける必要があります。
この設定では、タスクはクローズドセールスマン問題と呼ばれます。
まず、データを決定しましょう。 私たちの都市を10x10の正方形にランダムに散らばらせてください。 各都市は、それぞれ座標のペアで表されます。 わずか100都市。
次のコードを使用して、Matlabからデータを簡単に取得できます。
data = rand(2,100)*10;
他の言語では、ループを記述する必要がありますが、本質的には何も変わりません。 よく知られている関数rand（）で乱数を生成し、それらを10倍して、指定された領域に収まるようにします。
アニーリングのシミュレーションによる問題の解決
すべての都市のセットをCで示し、総数は| C |で示されます。 そして、私たちの場合、100に等しいです。各都市
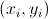対応するインデックス付き。
条件により、解決策はすべての都市間のルートです。つまり、状態セットSはすべての都市を通るすべての可能なルートです。 言い換えれば、すべての順序付けられたCの要素のシーケンスのセット
思い出すように、シミュレーテッドアニーリング法を使用するには、特定の各タスクに依存する2つの関数を定義する必要があります。 これは、エネルギーEの関数（または従来の用語では「目的関数」）と、新しい状態を生成する関数Fです。
距離を最小限に抑えるよう努めているため、「エネルギー」になります。 したがって、目的関数は次のようになります。
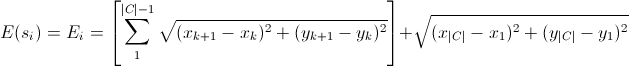
ルート内の都市のペア間のユークリッド距離の合計に過ぎません
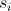。 タスクが閉じられたため、署名を強制されました 
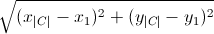最終的に、これは最後の都市と最初の都市の間の距離です。 もっと深くしなければ、ユークリッドは幾何学のレッスンで私たち全員が経験したポイント間のまさに距離です。 次の式で与えられます。
どこで
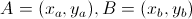
では、新しい状態をどのように取得するかを考えてみましょう。 最初に思い浮かぶのは、ルート上の任意の2つの都市を交換することです。 アイデアは正しいが、そのような変更は予測できない影響を与える
、メソッドは長時間機能しますが、正常に機能するわけではありません。
この場合の適切なオプションは、ルート内の任意の2つの都市を選択し、それらの間のパスを逆にすることです。 たとえば、ルート（1,2,3,4,5,6,7）がありました。 乱数ジェネレーターは都市2および7を選択し、手順を実行して（1,7,6,5,4,3,2）を受け取りました。
以下は、関数Fのコードです。
function [ seq ] = GenerateStateCandidate(seq) %seq - (), % - n = size(seq,1); % i = randi(n,1); % j = randi(n, 1);% if(i > j) seq(j:i) = flipud(seq(j:i)); % else seq(i:j) = flipud(seq(i:j));% end end
これで必要なものはすべて揃ったので、最適化プロセスを開始できます。 しかし、楽しい部分に進む前に、完全なプログラムコードを提供します。 上記の擬似コードの段落と比較することは非常に興味深いと思います。
function [ state ] = SimulatedAnnealing( cities, initialTemperature, endTemperature) n = size(cities,1); % state = randperm(n); % , % randperm(n) - 1 n currentEnergy = CalculateEnergy(state, cities); % T = initialTemperature; for i = 1:100000 % % T stateCandidate = GenerateStateCandidate(state); % - candidateEnergy = CalculateEnergy(stateCandidate, cities); % if(candidateEnergy < currentEnergy) % currentEnergy = candidateEnergy; % state = stateCandidate; else p = GetTransitionProbability(candidateEnergy-currentEnergy, T); % , if (MakeTransit(p)) % , currentEnergy = candidateEnergy; state = stateCandidate; end end; T = DecreaseTemperature(initialTemperature, i) ; % if(T <= endTemperature) % break; end; end end
ご覧のとおり、複雑なことは何もありません。
結果
アルゴリズムは確率的な性質を持っているため、ケースは「アニーリング」がローカルミニマムにとどまるように順序付けることができます。 したがって、いくつかの開始を行い、結果が収束する最小値に注意する価値があります。
プログラムは
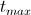= 10および 
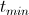= 0.00001。
この図は、最初の反復の状態を示しています。 私たちが彼にそのようなルートを提供したならば、セールスマンが大きな喜びを経験することはありそうにありません。
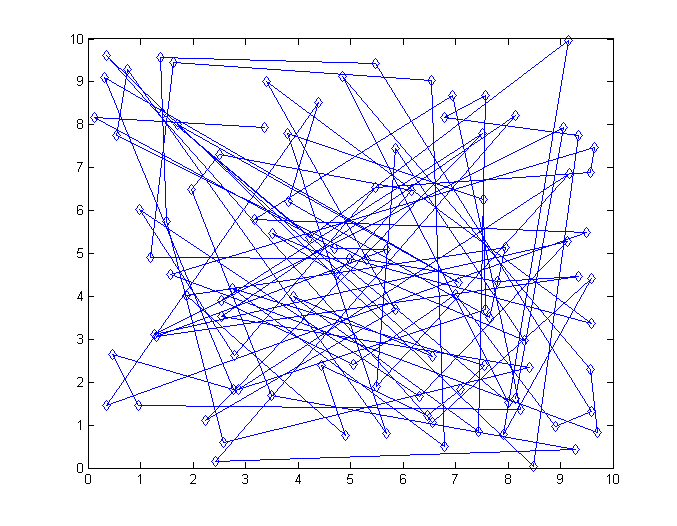
出力結果はより良く見えます：
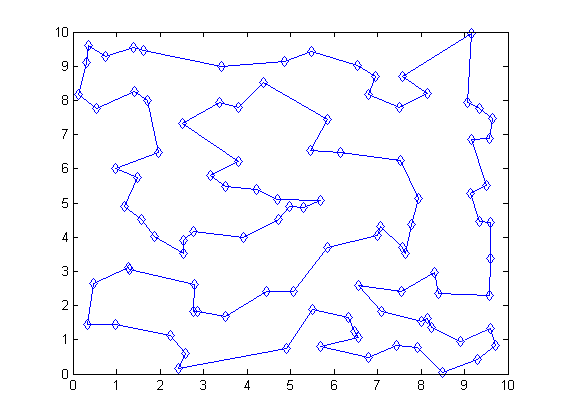
ただし、現在の実装のアルゴリズムは非常に効率的に機能する（徹底的な検索よりも確実に高速である）にもかかわらず、「品質」を損なうことなくはるかに優れた時間を達成できるという意見があります。 これを行うには、実用的なタスクとして、T関数を実験し、コメントで結果を共有することをお勧めします。
ソースコードはこちらからダウンロードできます 。
この読書があなたの役に立つことを願っています。 建設的な批判は大歓迎です。
PS
この機会に、Anna AntonovaとDmitry Ignatovに感謝したいと思います。AnnaAntonovaとDmitry Ignatovは、出版前にこの記事を読んで、良いアドバイスをくれました。