1年前の3日
コース「最適化方法」の実験室作業の1つとして、輸送問題の解決策を実装するように依頼されましたが、1つの小さな条件で、輸送はバッチで発生します。 これは、今では、従来の生産とは異なり、貨物の輸送（10個など）が支払われ、11個を輸送する必要がある場合でも、2ロット（11個は1つのトレーラーに収まらない）を支払うことを意味します。 ささいな追加のように思えますが、今どのように問題を解決し、少なくともそれを形式化する方法はありますか？ 応用数学科の学生として、私は偉大なgoogle.ruが何も知らなかったという事実に慣れていませんでしたが、彼の兄、英語を話すGoogle、または私が答えることができた最適化理論の本の闇のどちらでもなかったのは驚きでしたこの質問。
すぐに言いたい-私は自分のアルゴリズムでFields Awardを使用するふりをしません。 私は超自然的なことを提案しませんが、そのような問題を解決し始めたばかりの人のために、私は少し助けることができます。
Cを支払い行列、 aを貨物在庫のベクトル、 bを貨物の需要のベクトル、kをバッチ内の商品の数とします。 次の形式化を検討します。
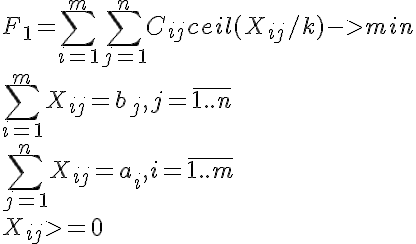
ここで、 Xは輸送行列、つまり 最適化されたパラメータ、ceil-最も近い整数に切り上げます。
さらに、考慮事項を紹介します。
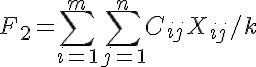
まず、F2-> minで古典的な輸送問題を解きます。 得られたF2の値は、許容値のセットのF1の下限です。 F2_save：= F2の値を思い出してください。 結果の解XでF1の値を見つけ、それをF1_save = F1として記憶します。 F1_save == ceil（F2_save）の場合、 Xは探しているソリューションです。それ以外の場合はさらに進んでください。
F1は、 Xの基底成分を最も近い倍数のk値に減らすことによってのみ減らすことができるため、追加の制限のある問題に対する解のツリーを構築します（分枝限定法）。 ツリーの一番上は、すでに受け取ったソリューションです。 ツリーの次の各層は、次のように構築されます。各基底成分（xij）が非多重k値（z）に等しい場合、古典的な輸送問題F2-> minを追加の制約xij = [z / k] * k（[x] x）の整数部分です（PSを参照）。 取得したソリューションのF1 <F1_saveの場合、F1_save：= F1。 得られた解に対してceil（F2）> = F1_saveの場合、この分岐は続行されません。 F1 == ceil（F2_save）の場合、結果のXは目的のソリューションです。それ以外の場合はさらに進みます。 したがって、決定ツリーを取得します。このブランチのシート上でceil（F2）> = F1_saveの場合、または基底からのすべてのコンポーネントがkの倍数である場合、または問題にまったく解決策がない場合、各ブランチは終了します。 F1_saveツリーを構築した後に取得した計画に対応する計画が最適です。
PS問題を再度解決するために制約を追加する必要はありません。 たとえば、考えられるすべてのF1減少サイクルを通過し、その中から最適なサイクルを選択できます。 または、デュアルシンプレックス法の方法を使用します。
例
非常に単純な例でアルゴリズムを検討してください。 k = 3、C = {{2,2}、{4,5}}、a = {2,3}、b = {2,3}とします。 したがって、ツリーの最上部は、目的関数F2を使用したこのような輸送問題の解決策です。
0）X = {{0,2}、{2,1}}、F2（X）〜= 5.67、F1（X）= 2 + 4 + 5 = 11。
F2_save：= 5.67、F1_save：= 11
なぜなら ceil（5.67）<11さらに進む-次のツリー層を構築します。
1.1）ノード0で解決される問題に条件x12 == 0を追加し、再度解決します。
X = {{2.0}、{0.3}}、F2（X）〜= 6.35、F1（X）= 2 + 5 = 7。
なぜなら F1 <F1_save（7 <11）、次にF1_save：= 7
なぜなら ceil（F2）> = F1_save（7> = 7）、このブランチを継続しない
なぜなら F1> ceil（F2_save）さらに進むと（おそらくより良い解決策があるかもしれません）、ブランチは続行しませんが、層はまだ終了していません。
1.2）ノード0で解決される問題に条件x21 == 0を追加し、再度解決します。
X = {{2.0}、{0.3}}、F2（X）〜= 6.35、F1（X）= 2 + 5 = 7。
なぜなら F1 == F1_save（7 == 7）、F1_saveは変更されません
なぜなら ceil（F2）> = F1_save（7> = 7）、このブランチを継続しない
なぜなら F1> ceil（F2_save）さらに進むと（おそらくより良い解決策があるかもしれません）、ブランチは続行しませんが、層はまだ終了していません。
1.3）ノード0で解決される問題に条件x22 == 0を追加し、再度解決します。 このような問題には解決策がありません=>そして、このブランチを継続しません。
基本的なコンポーネントはもう残っていない（層は終了している）ため、ブランチを続行する必要はありません（無意味で、より良いソリューションは得られません）。 F1_save == 7が最小コストです。 それらに対応する計画（彼が答えです）X = {{2,0}、{0,3}}