宇宙が始まる瞬間、つまりビッグバンから数えます。 最小限の数式とコード行の結果を得るために、多くの予約を省略します(はい、Pythonでプログラミングします!)。 ボーナスとして、宇宙にどれだけの暗黒エネルギーがあるかを推定します。

ハッブル宇宙望遠鏡で見た超新星1994D。 写真:ピート・シャリス-ハーバードスミソニアン天体物理学センター
好奇心が強い それでは行こう!
問題の物理的な側面について簡単に
ハッブルについて聞いたことがありますか? 彼にちなんで名付けられた望遠鏡もあります。 そこで彼は、宇宙のサイズが拡大しているという事実、あるいは、近くの銀河が散乱しているという事実を発見しました。 宇宙はどのように成長しますか? 類推は簡単かもしれません。 自分が膨らまされている気球のアリだと想像してください。 あなたの体には何も起こりませんが、世界はゆっくりと拡大しており、ボール上の他のアリはどんどん遠くなっているように見えます。
ハッブルに戻る。 彼はどのようにしてこの事実を確立したのですか? 2つのポイントがあります。
- 最初に、銀河の速度を測定する必要があります。 ここでは、ドップラー効果が必要です。 プラットフォームに沿ってスイープする瞬間に口trainを吹くという古典的な実験については、誰もが知っています。 物体が私たちから遠ざかると、その物体が発する波長は長くなります。 この修正から速度を見つけることができます。 天文学では、この増加は赤方偏移と呼ばれ、文字zで示されます。 既知のスペクトル線を観察し、その変位を見つけて速度を計算します。
- 第二に、銀河までの距離。 彼らとの距離が測定できないという理由だけで。 ここで、追加のオブジェクト-タイプIa超新星がすでに必要です。 これらはそのような星の爆発で、同じ量のエネルギーが放出されます。 観測した明るさから、爆発自体とこの爆発が発生した銀河までの距離を計算できます。 上の写真は銀河と超新星爆発です。 明るさの点では、銀河全体を超えています。銀河では、約1億の星があります。
そして、宇宙の年齢はどこですか?
ユニバースの成長速度を測定することで、それがポイントであった時期を把握できます。 この瞬間はすべての始まりと呼ばれ、何年前かを推定することができます。
システムを準備する
Pythonが必要になります(バージョンは重要ではありません。2.7を使用します。3との違いは最小限です)。
sudo apt-get install python
計算には、 NumpyとScipyを使用します。
pip install numpy
pip install scipy
Matplotlibチャートの場合:
pip install matplotlib
ルートのない紳士には、そのようなアセンブリをお勧めします: store.continuum.io/cshop/anaconda
Windowsユーザーの場合: code.google.com/p/pythonxy
システムが準備されたと信じています。 さらに進むものはすべて、インタラクティブに(Pythonコンソールで直接)、またはiPythonで起動できます。 あなたが好きな人。
データをダウンロードする
現代の天体物理学の美しさは、観測データの完全な開放性です。 上で書いたタイプIa超新星のカタログを使用します: supernova.lbl.gov/Union
このファイルが必要です: supernova.lbl.gov/Union/figures/SCPUnion2.1_mu_vs_z.txt
コードの書き始め
後で必要になるライブラリを接続します。
import numpy as np import matplotlib.pyplot as plt
ファイルからデータをロードし、3つの補助配列を作成します。
# 5 , . # 0 , , data=np.loadtxt('SCPUnion2.1_mu_vs_z.txt',skiprows=5,converters={0: lambda s: 0}) # z = data[:,1] # distance modulus DM = data[:,2] DM_err=data[:,3]
距離モジュラスとは何か、そしてそれからオブジェクトまでの距離を取得する方法は、 ベラルーシのウィキペディアに簡潔に書かれています。
私たちはこの量を、オブザーバーの利便性によってのみ存在するものを物理的なものに変換します。 オブジェクトまでの距離は、 DL配列に書き込まれます。
# def DM2DL(DM): return 10**(DM/5-1)/1e4 # DL=DM2DL(DM)
距離係数を計算するとき、カタログの著者は、超新星の光度が-19.3であることを提案しました。これは説明で説明されています。 彼らは私たちのためにこの仕事をしました。
変数zには赤方偏移があり、 DLにはMegaparsec の距離があります(1パーセク= 3e16メートル= 3.3光年)。 写真を作成して、何が起こったのかを確認できます。
plt.plot(DL,z,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$z$',size=18)

それでは、赤方偏移zを速度に変換しましょう。 まず、速度を赤方偏移に変換する関数、つまり逆関数が必要です。
# # c=29979245800 # cm/s # def v2z(v): return sqrt((1.0+v/c)/(1.0-v/c))-1.0
公式はここから取得されます: en.wikipedia.org/wiki/Redshift#Redshift_formulae
逆方向の変換では、z_listとv_listの対応を事前に計算し、その後、ポイント間を補間する関数を作成します。
v_list=linspace(0,c,100) z_list=v2z(v_list) # plt.plot(z_list,v_list) def z2v(z): return np.interp(z,z_list,v_list)/1e5 v=z2v(z) # km/s
オブジェクトからの距離に応じてオブジェクトの速度を見てみましょう。
plt.plot(DL,v,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$v\;\mathrm{[km/s]}$',size=18)
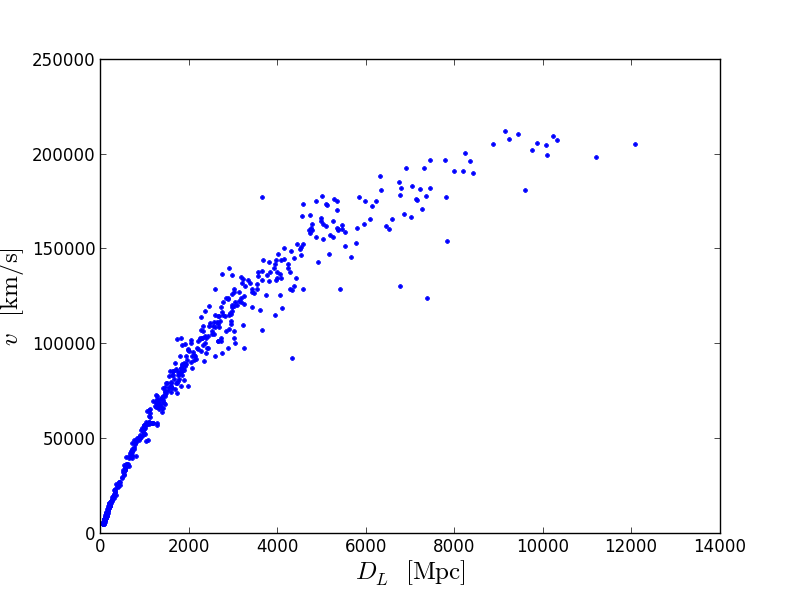
この写真は、オブジェクトが遠ざかるほど、オブジェクトから離れる速度が速くなることを明確に示しています。 利益を上げましょう。 ポイント0での直線(微分)の勾配は、ハッブル定数Hと呼ばれ、km / s / Mpsで測定されます。 このスロープはフィッティングによって見つけることができますが、簡単な方法で進めます。 斜面を選ぶだけです:
plt.plot(DL,v,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$v\;\mathrm{[km/s]}$',size=18) temp=np.array([0.0,20.0]) plt.plot(temp,50.0*temp,'r') plt.plot(temp,70.0*temp,'g') plt.plot(temp,100.0*temp,'m') plt.legend(('data','H=50','H=70','H=100'))
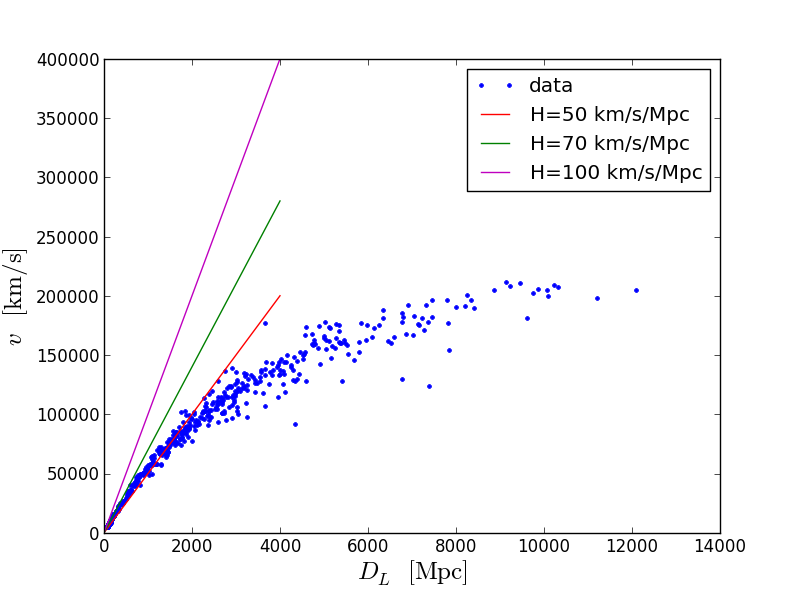
拡大版:
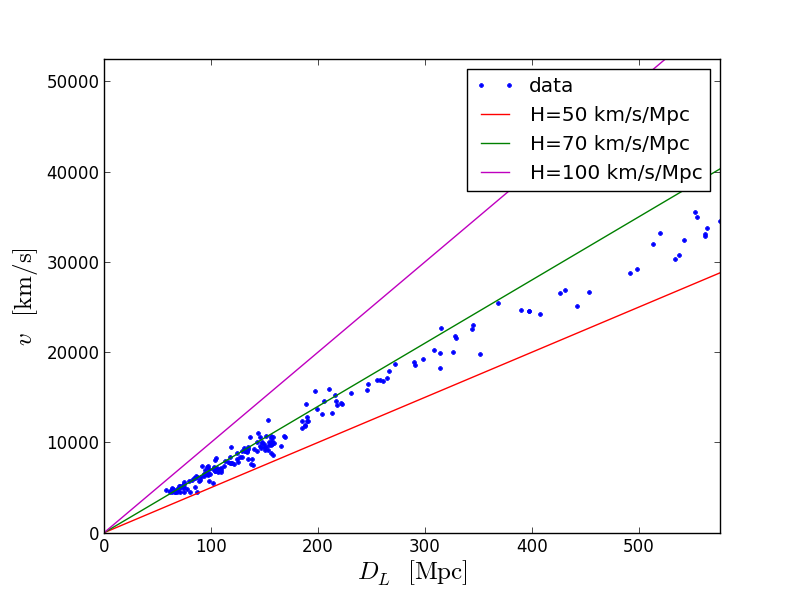
最も正確な推測:H = 70 km / s / Mps。 つまり、私たちから1 Mpc離れた場所にあるオブジェクトは、70 km / sの速度で移動しています。 言い換えれば、彼と私は何年も前に同じポイントにいた(分散速度が一定であると仮定):
(1 Mpc)/(70 km / s)= 1 / H = 14,000,000,000年前
( Googleはさまざまな測定単位を変換するのに適しています。)
合計で、数行のコードを実行した後、宇宙の年齢は約140億年であることがわかりました。 まず、これは非常に大まかな評価です。 第二に、実験で行うべき測定誤差を評価しませんでした。 また、超新星爆発の明るさをどのように知っているのか、そしてそれらを同じと考える理由も述べていません。 これらもまた興味深いトピックです。 それでも、このような大まかな評価は良い結果をもたらします! すべての既知の観測値を使用したより正確な分析では、13.813±0.058十億年の結果が得られます。
ハッブルはかつてそのような図の最初の部分のみを観察しました(彼の1929年の記事apod.nasa.gov/diamond_jubilee/d_1996/hub_1929.htmlから )

70の代わりに500という数字を取得しました。それにもかかわらず、エラーは10回未満であり、ヒットに対して保護されています。
ダークエネルギー?
図では、線が図の先頭にのみ収まることがわかります。 さらに、線形近似はまったく適合しません。 次のステップのために、宇宙論について少し掘り下げる必要があります。 最も単純なモデルでは、宇宙は物質と暗黒エネルギー(アインシュタインのラムダ項)で構成され、平坦です。 Omega_Mの物質とOmega_Lの暗黒エネルギーからの宇宙の他の部分、およびOmega_M + Omega_L = 1で構成される宇宙の部分を指定することにより、式を使用して赤方偏移を通じて物体までの距離を表現できます(詳細はWikipediaで読むことができます: [1] [2] ):
補助関数E(z)を導入します。
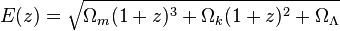
ここに表示されるOmega_kは、宇宙の曲率の原因です。 簡単にするために、フラット、つまりOmega_k = 0と考えます。 したがって、次の式では、中央の行が必要です。
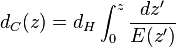
主要な積分
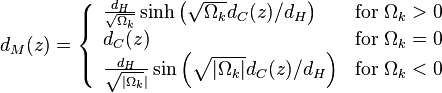
追加要因(1 + z)、その起源は説明するには長すぎます:):

次に、積分を計算するコードを記述します。
# E_z def e_Z(z, OmegaM): OmegaL=1.0-OmegaM return (OmegaM*(1.0+z)**3+OmegaL)**(-0.5) # scipy import scipy.integrate as si # def D_L(z, OmegaM): dh=4286.0 # c/H, H 70 // D_c=dh*si.quad(e_Z,0.0,z,args=(OmegaM))[0] return D_c*(1.0+z) # , def D_L_batch(z,OmegaM,H): DL=z.copy() for i in range(len(z)): DL[i]=D_L(z[i],OmegaM,H) return DL # plt.plot(DL,v,'.') plt.xlabel(r'$D_{L}\;\mathrm{[Mpc]}$',size=18) plt.ylabel(r'$v\;\mathrm{[km/s]}$',size=18) # z- 0 1.5, 100 temp_z=np.linspace(0,1.5,100) # v- temp_v=z2v(temp_z) # Omega_M plt.plot(D_L_batch(temp_z,0.01,70.0),temp_v,'r') plt.plot(D_L_batch(temp_z,0.27,70.0),temp_v,'g') plt.plot(D_L_batch(temp_z,0.99,70.0),temp_v,'m') plt.legend(('data',r'$\Omega_M=0.01$',r'$\Omega_M=0.27$',r'$\Omega_M=0.99$'),loc=4)
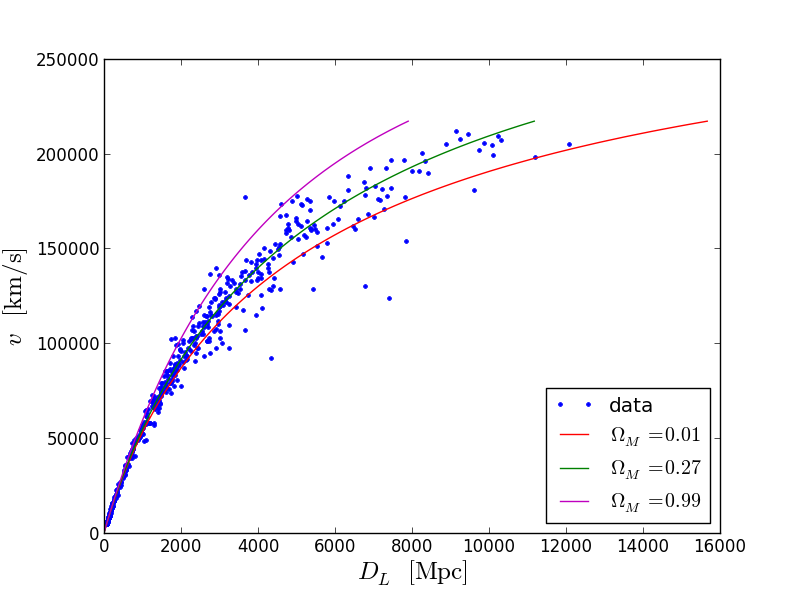
緑色の曲線は、データによりやや適合しています。 繰り返しになりますが、簡単にするために、理論をデータに入力する際のエラーについては忘れています。 結論は次のとおりです。 現在、暗黒エネルギーと物質の量は同程度です(100対1の比率がデータに適合しないモデル)。 これはかなり興味深い事実です。 宇宙の約70%は一種の暗黒エネルギーであり、その性質はまだ理解されていません。 残りの約30%の問題も、見かけほど単純ではありません。 その5分の1だけがバリオン物質(私たちが構成しているもの)で、残りはダークマターです。 彼女については、その量はまた別の時に推定することができます。
さて、ここにいます。 最後に、これは宇宙の幾何学と年齢を測定する唯一の方法とは程遠いというだけです。 それらのいくつかがあります。 そして驚くべきことに、彼らはすべてビッグバン理論と拡大する宇宙を支持して語っています。
イエス様、紳士の名前の幸せなお祝い! :)