今日の記事では、Pythonとstatsmodelsモジュールを使用して時系列を分析するプロセスを説明しようとします。 このモジュールは、統計分析と計量経済学を実施するための幅広いツールと方法を提供します。 そのようなシリーズの分析の主要な段階を示してみます;結論として、 ARIMAモデルを構築します。
例として、モスクワ地域の倉庫複合施設の売上高に関する実際のデータが取得されます。
データをダウンロードして前処理する
開始するには、データをアップロードして確認します。
from pandas import read_csv, DataFrame import statsmodels.api as sm from statsmodels.iolib.table import SimpleTable from sklearn.metrics import r2_score import ml_metrics as metrics In [2]: dataset = read_csv('tovar_moving.csv',';', index_col=['date_oper'], parse_dates=['date_oper'], dayfirst=True) dataset.head()
| オトグルスカ | プリエムカ | |
|---|---|---|
| date_oper | ||
| 2009-09-01 | 179667 | 276712 |
| 2009-09-02 | 177670 | 164999 |
| 2009-09-03 | 152112 | 189181 |
| 2009-09-04 | 142938 | 254581 |
| 2009-09-05 | 130741 | 192486 |
したがって、この場合はread_csv（）関数を見ることができるように、使用する列とインデックスを指定するパラメーターを指定することに加えて、日付を操作するためのパラメーターがさらに3つあります。 それらについて詳しく見ていきましょう。
parse_datesは、 DateTime型に変換される列名を指定します。 この列に空の値が含まれている場合、解析が失敗し、 オブジェクト型の列が返されることに注意してください。 これを回避するには、 keep_default_na = Falseパラメーターを追加します。
最後のdayfirstパラメーターは、解析関数に、行の最初がその日に行くことであり、その逆ではないことを伝えます。 このパラメーターが設定されていない場合、関数は日付を正しく変換せず、場所の月と日を混同しない場合があります。 たとえば、 02/01/2013は02-01-2013に変換されますが 、これは正しくありません。
出荷の値を含む時系列の別のシリーズを選択します。
otg = dataset.Otgruzka otg.head()
| date_oper | |
| 2009-09-01 | 179667 |
| 2009-09-02 | 177670 |
| 2009-09-03 | 152112 |
| 2009-09-04 | 142938 |
| 2009-09-05 | 130741 |
| 名前：Otgruzka、dtype：int64 | |
これで時系列が作成され、その分析に進むことができます。
時系列分析
始めるために、シリーズのグラフをソートしましょう：
otg.plot(figsize=(12,6))
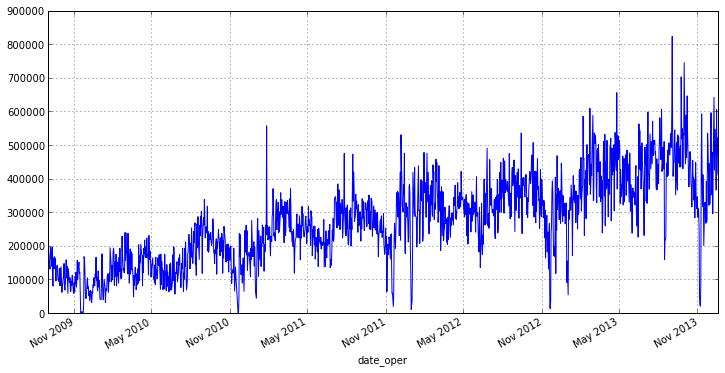
グラフから、私たちのシリーズはスプレッドに影響する少数の排出物があることがわかります。 さらに、毎日の出荷を分析することは完全に正しいわけではありません。たとえば、週の終わりまたは初めに、商品が他の出荷よりもはるかに多く出荷される日があるためです。 したがって、毎週の間隔とその上での出荷の平均値に移動することは理にかなっています。これにより、排出量を節約し、範囲の変動を減らすことができます。 pandasでは、このために便利なresample（）関数があります。パラメーターとして、丸め期間と集約関数が渡されます。
otg = otg.resample('W', how='mean') otg.plot(figsize=(12,6))
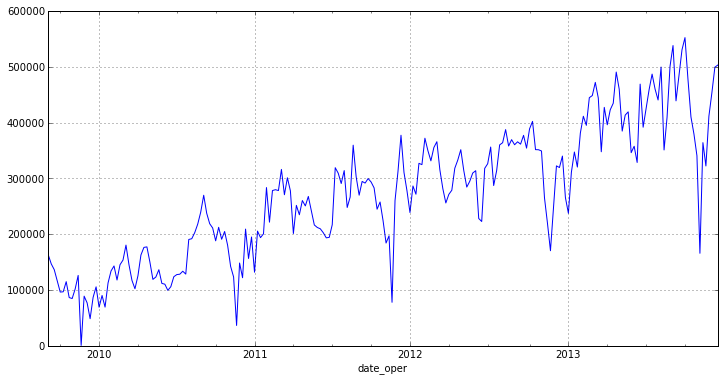
ご覧のとおり、新しいチャートには明るい放射はなく、顕著な傾向があります。 このことから、系列は定常的ではないと結論付けることができます[1] 。
itog = otg.describe() otg.hist() itog
| 数える | 225 |
| 意地悪 | 270858.285365 |
| 標準 | 118371.082975 |
| 分 | 872.857143 |
| 25％ | 180263.428571 |
| 50％ | 277898.714286 |
| 75％ | 355587.285714 |
| 最大 | 552485.142857 |
| dtype：float64 | |
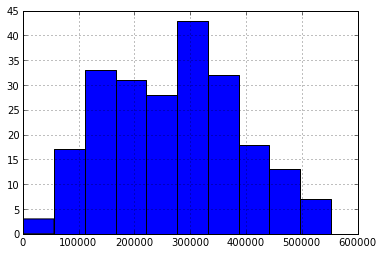
特性とヒストグラムからわかるように、変動係数から明らかなように、シリーズの均質性は低く、散布は比較的小さくなっています。
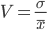どこで 
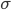- 標準偏差 
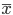-サンプルの算術平均。 私たちの場合、それは次と等しい：
print 'V = %f' % (itog['std']/itog['mean'])
V = 0.437022
Harkey -Behr検定を実行して分布の名目性を決定し、均質性の仮定を確認します。 これを行うために、この統計の値を返す関数jarque_bera（）があります。
row = [u'JB', u'p-value', u'skew', u'kurtosis'] jb_test = sm.stats.stattools.jarque_bera(otg) a = np.vstack([jb_test]) itog = SimpleTable(a, row) print itog
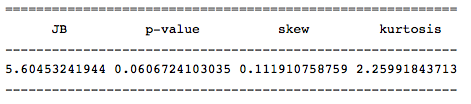
この統計の値は、分布の正規性の帰無仮説が低い確率（ おそらく0.05を超える ）で拒否されることを示しているため、系列には正規分布があります。
SimpleTable（）関数を使用して、出力をフォーマットします。 この場合、値の配列（2次元以下）と列または行の名前のリストを受け取ります。
多くの方法とモデルはシリーズの定常性に関する仮定に基づいていますが、前述のように、シリーズはそうではない可能性が高いです。 したがって、定常性テストを確認するために、ユニットルートの存在について一般化されたDickey-Fullerテストを実施しましょう。 このために、 statsmodelsモジュールにadfuller（）関数があります。
test = sm.tsa.adfuller(otg) print 'adf: ', test[0] print 'p-value: ', test[1] print'Critical values: ', test[4] if test[0]> test[4]['5%']: print ' , ' else: print ' , '
adf：-1.38835541357
p値：0.58784577297
クリティカル値：{'5％'：-2.8753374677799957、 '1％'：-3.4617274344627398、'10％ '：-2.5741240890815571}
単一の根があり、列は静止していません
実行されたテストにより、系列の非定常性の仮定が確認されました。 多くの場合、系列の差をとることでこれが可能になります（たとえば、系列の最初の差が定常的である場合、 統合1次系列と呼ばれます）。
それでは、 シリーズの統合シリーズの順序を定義しましょう。
otg1diff = otg.diff(periods=1).dropna()
上記のコードでは、 diff（）関数は、指定された期間オフセットの隣にある元の系列の差を計算します。 オフセット期間は期間パラメーターとして渡されます。 なぜなら 最初の値はあいまいなので、このためにそれを取り除く必要があり、dropna（）メソッドが使用されます。
結果のシリーズの定常性を確認します。
test = sm.tsa.adfuller(otg1diff) print 'adf: ', test[0] print 'p-value: ', test[1] print'Critical values: ', test[4] if test[0]> test[4]['5%']: print ' , ' else: print ' , '
adf：-5.95204224907
p値：2.13583392404e-07
クリティカル値：{'5％'：-2.8755379867788462、 '1％'：-3.4621857592784546、'10％ '：-2.574231080806213}
単一の根はなく、列は静止しています
上記のコードからわかるように、結果の一連の最初の違いは定常的なものに近づきました。 確かに、それをいくつかのギャップに分割し、マットを確認します。 異なる間隔での期待：
m = otg1diff.index[len(otg1diff.index)/2+1] r1 = sm.stats.DescrStatsW(otg1diff[m:]) r2 = sm.stats.DescrStatsW(otg1diff[:m]) print 'p-value: ', sm.stats.CompareMeans(r1,r2).ttest_ind()[1]
p値：0.693072039563
p値が高いと 、平均が等しいという帰無仮説が真であると断言できます。これは、系列の定常性を示しています。 この傾向がないことを確認するために、新しいシリーズのグラフを作成します。
otg1diff.plot(figsize=(12,6))
トレンドは実際に存在しないため、最初の差異の系列は定常的であり、最初の系列は1次の統合系列です 。
時系列モデルの構築
モデリングには、多くの最初の違いのために構築されたARIMAモデルを使用します。
そのため、モデルを構築するには、2つのパラメーターで構成されるその順序を知る必要があります。
パラメータdは1を破り、 pとqを決定するために残ります。 それらを決定するには、いくつかの最初の違いについて、 自己相関（ACF）および部分自己相関（PACF）関数を調べる必要があります。
ACFはqを決定するのに役立ちます。なぜなら、そのコレログラムによって、 MAモデルの0とは非常に異なる自己相関係数の数を決定できるからです。
PACFはpを決定するのに役立ちます。なぜなら、そのコレログラムによって、 ARモデルの0とは非常に異なる最大係数数を決定できるからです。
対応するコレログラムを作成するために、statsmodelsパッケージで使用可能な関数plot_acf（）およびplot_pacf（）を使用できます。 これらは、 ACFおよびPACFグラフを表示します。 このグラフでは、ラグ数がX軸に沿ってプロットされ、対応する関数の値がY軸に沿ってプロットされます。 関数のラグの数が重要な係数の数を決定することに注意してください。 したがって、関数は次のようになります。
ig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(otg1diff.values.squeeze(), lags=25, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(otg1diff, lags=25, ax=ax2)
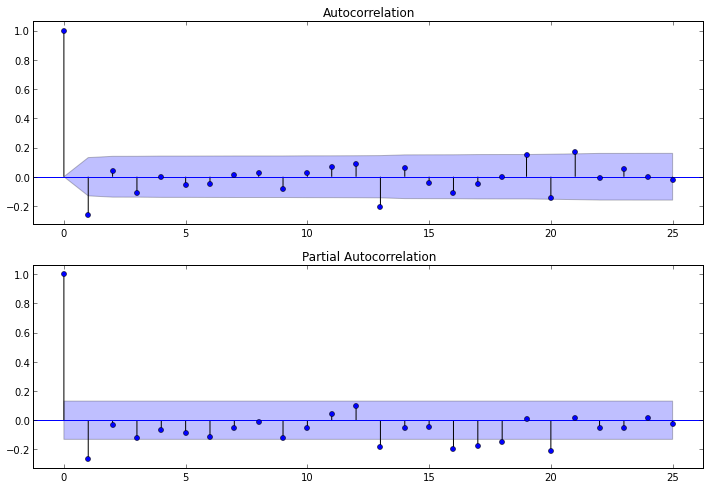
PACFコレログラムを調べた後、 p = 1と結論付けることができます。 わずか1ラグだけがゼロと大きく異なります。 ACFコレログラムから、 q = 1であることがわかります。 ラグ1の後、関数の値は急激に低下します。
したがって、すべてのパラメーターがわかっている場合、モデルを構築することは可能ですが、その構築のために、すべてのデータではなく、一部のみを取得します。 モデルの予測の精度を検証するために、モデルに分類されなかった部分のデータを残します。
src_data_model = otg[:'2013-05-26'] model = sm.tsa.ARIMA(src_data_model, order=(1,1,1), freq='W').fit(full_output=False, disp=0)
傾向パラメーターは、モデル内の定数の存在を担当します。 結果のモデルに関する情報を導き出します。
print model.summary()
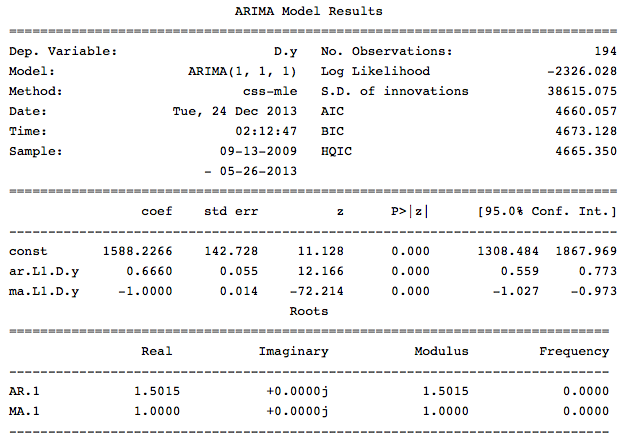
モデルのこの情報からわかるように、すべての係数は重要であり、モデルの評価に進むことができます。
モデルの分析と評価
このモデルの残りの部分が「ホワイトノイズ」に準拠しているかどうかを確認し、残差のコレログラムも分析します。これにより、予測に含める重要な回帰要素を決定できるようになります。
したがって、最初に行うことは、残差がランダムである、つまり「ホワイトノイズ」であるという仮説をテストするために、 肺–ボックスQ検定を実施することです。 このテストは、 ARIMAモデルの残りに対して実行されます。 したがって、最初にモデルの残りを取得し、それらのACFを構築してから、結果の係数のテストを行う必要があります。 statsmadelsを使用すると、これは次のように実行できます。
q_test = sm.tsa.stattools.acf(model.resid, qstat=True) # resid, , qstat=True, - print DataFrame({'Q-stat':q_test[1], 'p-value':q_test[2]})
結果
| Q-stat | p値 | |
|---|---|---|
| 0 | 0.531426 | 0.466008 |
| 1 | 3.073217 | 0.215109 |
| 2 | 3.644229 | 0.302532 |
| 3 | 3.906326 | 0.418832 |
| 4 | 4.701433 | 0.453393 |
| 5 | 5.433745 | 0.489500 |
| 6 | 5.444254 | 0.605916 |
| 7 | 5.445309 | 0.709091 |
| 8 | 5.900762 | 0.749808 |
| 9 | 6.004928 | 0.814849 |
| 10 | 6.155966 | 0.862758 |
| 11 | 6.299958 | 0.900213 |
| 12 | 12.731542 | 0.468755 |
| 13 | 14.707894 | 0.398410 |
| 14 | 20.720607 | 0.145996 |
| 15 | 23.197433 | 0.108558 |
| 16 | 23.949801 | 0.120805 |
| 17 | 24.119236 | 0.151160 |
| 18 | 25.616184 | 0.141243 |
| 19 | 26.035165 | 0.164654 |
| 20 | 28.969880 | 0.114727 |
| 21 | 28.973660 | 0.145614 |
| 22 | 29.017716 | 0.179723 |
| 23 | 32.114006 | 0.124191 |
| 24 | 32.284805 | 0.149936 |
| 25 | 33.123395 | 0.158548 |
| 26 | 33.129059 | 0.192844 |
| 27 | 33.760488 | 0.208870 |
| 28 | 38.421053 | 0.113255 |
| 29日 | 38.724226 | 0.132028 |
| 30 | 38.973426 | 0.153863 |
| 31 | 38.978172 | 0.184613 |
| 32 | 39.318954 | 0.207819 |
| 33 | 39.382472 | 0.241623 |
| 34 | 39.423763 | 0.278615 |
| 35 | 40.083689 | 0.293860 |
| 36 | 43.849515 | 0.203755 |
| 37 | 45.704476 | 0.182576 |
| 38 | 47.132911 | 0.174117 |
| 39 | 47.365305 | 0.197305 |
これらの統計値とp値の値は、残基のランダム性の仮説が拒否されないことを示しており、このプロセスは「ホワイトノイズ」を表している可能性が高いです。
では、決定係数を計算しましょう
このモデルが説明する観測の割合を理解するには：
pred = model.predict('2013-05-26','2014-12-31', typ='levels') trn = otg['2013-05-26':] r2 = r2_score(trn, pred[1:32]) print 'R^2: %1.2f' % r2
R ^ 2：-0.03
モデルの標準偏差[2] ：
metrics.rmse(trn,pred[1:32])
80919.057367642512
予測の平均絶対誤差[2] ：
metrics.mae(trn,pred[1:32])
63092.763277651895
チャートに予測を描画することは残っています。
otg.plot(figsize=(12,6)) pred.plot(style='r--')
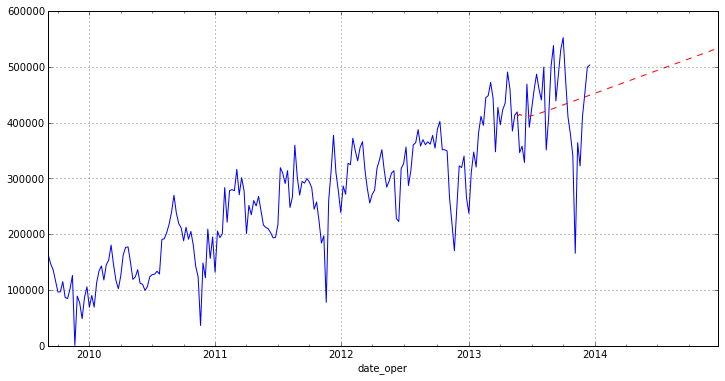
おわりに
グラフからわかるように、このモデルはあまり良い予測をしていません。 これは、完全に削除されていないソースデータの外れ値と、まったく新しいため 、 statsmodelsパッケージのARIMAモジュールが原因です。 この記事の目的は、Pythonで時系列を正確に分析する方法を示すことです。 また、今日調査したパッケージでは、さまざまな回帰分析方法が非常に完全に実装されていることにも注意したいと思います（今後の記事で紹介します）。
一般に、小規模な研究にはstatsmodelsパッケージが完全に適していますが、本格的な科学研究にはまだ生であり、いくつかのテストと統計が欠落しています。
参照資料
- I.I. エリゼエバ。 計量経済学
- 時系列モデルの比較