はじめに
こんにちは、読者の皆様。
過去の記事の実際の例では、分類の問題（ クレジットスコアリングの問題 ）とテキスト情報分析の基本（ パスポートの問題 ）を解決する方法を示しました。 今日は、別のクラスの問題、つまり回帰復元に触れたいと思います。 このクラスのタスクは通常、 予測に使用されます。
予測の問題を解決する例として、最大のUCIリポジトリからEnergy Efficiencyデータセットを取得しました。 伝統として、Pythonとpandasおよびscikit-learn分析パッケージを使用します。
データセットの説明と問題の説明
次の部屋の属性を説明するデータセットが提供されます。
| フィールド | 説明 | 種類 |
|---|---|---|
| X1 | 比較的コンパクト | フロート |
| X2 | 面積 | フロート |
| X3 | 壁面積 | フロート |
| X4 | 天井面積 | フロート |
| X5 | 全高 | フロート |
| X6 | オリエンテーション | INT |
| X7 | グレージングエリア | フロート |
| X8 | 分散ガラスエリア | INT |
| y1 | 加熱負荷 | フロート |
| y2 | 冷房負荷 | フロート |
その中に
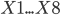-分析が実行される基礎となる施設の特性 
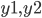-予測される負荷値。
予備データ分析
開始するには、データをアップロードして確認してください。
from pandas import read_csv, DataFrame from sklearn.neighbors import KNeighborsRegressor from sklearn.linear_model import LinearRegression, LogisticRegression from sklearn.svm import SVR from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import r2_score from sklearn.cross_validation import train_test_split dataset = read_csv('EnergyEfficiency/ENB2012_data.csv',';') dataset.head()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 2 | 0 | 0 | 15.55 | 21.33 |
| 1 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 3 | 0 | 0 | 15.55 | 21.33 |
| 2 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 4 | 0 | 0 | 15.55 | 21.33 |
| 3 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 5 | 0 | 0 | 15.55 | 21.33 |
| 4 | 0.90 | 563.5 | 318.5 | 122.50 | 7 | 2 | 0 | 0 | 20.84 | 28.28 |
次に、関連する属性があるかどうかを確認します。 これは、すべての列の相関係数を計算することで実行できます。 これを行う方法は、以前の記事で説明されています 。
dataset.corr()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 1.000000e + 00 | -9.919015e-01 | -2.037817e-01 | -8.688234e-01 | 8.277473e-01 | 0.000000 | 1.283986e-17 | 1.764620e-17 | 0.622272 | 0.634339 |
| X2 | -9.919015e-01 | 1.000000e + 00 | 1.955016e-01 | 8.807195e-01 | -8.581477e-01 | 0.000000 | 1.318356e-16 | -3.558613e-16 | -0.658120 | -0.672999 |
| X3 | -2.037817e-01 | 1.955016e-01 | 1.000000e + 00 | -2.923165e-01 | 2.809757e-01 | 0.000000 | -7.969726e-19 | 0.000000e + 00 | 0.455671 | 0.427117 |
| X4 | -8.688234e-01 | 8.807195e-01 | -2.923165e-01 | 1.000000e + 00 | -9.725122e-01 | 0.000000 | -1.381805e-16 | -1.079129e-16 | -0.861828 | -0.862547 |
| X5 | 8.277473e-01 | -8.581477e-01 | 2.809757e-01 | -9.725122e-01 | 1.000000e + 00 | 0.000000 | 1.861418e-18 | 0.000000e + 00 | 0.889431 | 0.895785 |
| X6 | 0.000000e + 00 | 0.000000e + 00 | 0.000000e + 00 | 0.000000e + 00 | 0.000000e + 00 | 1.000000 | 0.000000e + 00 | 0.000000e + 00 | -0.002587 | 0.014290 |
| X7 | 1.283986e-17 | 1.318356e-16 | -7.969726e-19 | -1.381805e-16 | 1.861418e-18 | 0.000000 | 1.000000e + 00 | 2.129642e-01 | 0.269841 | 0.207505 |
| X8 | 1.764620e-17 | -3.558613e-16 | 0.000000e + 00 | -1.079129e-16 | 0.000000e + 00 | 0.000000 | 2.129642e-01 | 1.000000e + 00 | 0.087368 | 0.050525 |
| Y1 | 6.222722e-01 | -6.581202e-01 | 4.556712e-01 | -8.618283e-01 | 8.894307e-01 | -0.002587 | 2.698410e-01 | 8.736759e-02 | 1.000000 | 0.975862 |
| Y2 | 6.343391e-01 | -6.729989e-01 | 4.271170e-01 | -8.625466e-01 | 8.957852e-01 | 0.014290 | 2.075050e-01 | 5.052512e-02 | 0.975862 | 1.000000 |
マトリックスからわかるように、次の列は互いに相関しています（相関係数の値は95％以上です）。
- y1-> y2
- x1-> x2
- x4-> x5
それでは、選択から削除できるペアの列を選択しましょう。 これを行うには、各ペアで、 Y1とY2の予測値により大きな影響を与える列を選択し、それらを残して、残りを削除します。
ご覧のとおり、 y1 、 y2に相関係数を持つ行列は、X1とX4 よりもX2とX5が多いため、最後の列を削除できます。
dataset = dataset.drop(['X1','X4'], axis=1) dataset.head()
さらに、フィールドY1とY2は互いに非常に密接に相関していることがわかります 。 ただし、両方の値を予測する必要があるため、「現状のまま」にしておきます。
モデル選択
サンプルから予測値を分離します。
trg = dataset[['Y1','Y2']] trn = dataset.drop(['Y1','Y2'], axis=1)
データを処理した後、モデルの構築に進むことができます。 モデルを構築するには、次の方法を使用します。
これらの方法の理論は、機械学習に関するK.V. Vorontsovの講義で読むことができます。
決定係数 （ R-squared ）を使用して推定します。 この係数は次のように決定されます。
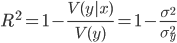
どこで
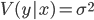-因子xの従属量yの条件付き分散。
係数の値は
また、1に近いほど、依存性が強くなります。
さて、これでモデルの構築とモデルの選択に直接進むことができます。 さらに分析しやすいように、すべてのモデルを1つのリストに入れましょう。
models = [LinearRegression(), # RandomForestRegressor(n_estimators=100, max_features ='sqrt'), # KNeighborsRegressor(n_neighbors=6), # SVR(kernel='linear'), # LogisticRegression() # ]
モデルの準備ができたので、初期データをtestとtrainingの 2つのサブサンプルに分割します。 私の以前の記事を読んだ人は、これはscikit-learnパッケージのtrain_test_split（）関数を使用して実行できることを知っています。
Xtrn, Xtest, Ytrn, Ytest = train_test_split(trn, trg, test_size=0.4)
さて、2つのパラメータを予測する必要があるので
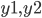、それぞれの回帰を作成する必要があります。 さらに、さらに分析するために、一時的なDataFrameに結果を書き込むことができます。 次の方法で実行できます。
# TestModels = DataFrame() tmp = {} # for model in models: # m = str(model) tmp['Model'] = m[:m.index('(')] # for i in xrange(Ytrn.shape[1]): # model.fit(Xtrn, Ytrn[:,i]) # tmp['R2_Y%s'%str(i+1)] = r2_score(Ytest[:,0], model.predict(Xtest)) # DataFrame TestModels = TestModels.append([tmp]) # TestModels.set_index('Model', inplace=True)
上記のコードからわかるように、係数を計算するには
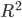r2_score（）関数が使用されます。
したがって、分析用のデータが取得されました。 グラフを作成して、どのモデルが最良の結果を示したかを見てみましょう。
fig, axes = plt.subplots(ncols=2, figsize=(10,4)) TestModels.R2_Y1.plot(ax=axes[0], kind='bar', title='R2_Y1') TestModels.R2_Y2.plot(ax=axes[1], kind='bar', color='green', title='R2_Y2')
結果と結論の分析
上記のグラフから、 RandomForestメソッド（ランダムフォレスト）が他のタスクよりもタスクをうまく処理したと結論付けることができます。 その決定係数は、両方の変数で他のものよりも高くなっています。
さらに分析するために、モデルを再トレーニングしましょう。
model = models[1] model.fit(Xtrn, Ytrn)
よく調べてみると、以前に依存サンプルYtrnを変数（列）に分割したのになぜ今は分割しないのかという疑問が生じる場合があります。
実際には、 RandomForestRegressorなどの一部のメソッドは複数の予測変数を処理できますが、他のメソッド（たとえばSVR ）は1つの変数のみを処理できます。 したがって、以前のトレーニングでは、一部のモデルを構築するプロセスでのエラーを回避するために列ブレークを使用しました。
もちろん、モデルを選択するのは良いことですが、各因子が予測値にどのように影響するかについての情報があれば良いでしょう。 このため、モデルにはfeature_importances_プロパティがあります。
これを使用して、最終モデルの各因子の重みを確認できます。
model.feature_importances_
配列（[0.40717901、0.11394948、0.34984766、0.00751686、0.09158358、
0.02992342]）
私たちの場合、全体の高さと面積が、加熱と冷却中の負荷に最も影響することがわかります。 予測モデルへの合計貢献度は約72％です。
また、上記のスキームによれば、各要因が加熱と冷却に別々に影響を与えることがわかりますが、これらの要因は非常に密接に相関しているため（
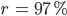）、私たちはそれらの両方について一般的な結論を出しました。
おわりに
この記事では、Pythonと分析パッケージpandasおよびscikit-learnを使用して、データの回帰分析の主な段階を表示しようとしました。
データセットは、可能な限り形式化されるように特別に選択されており、入力データの初期処理は最小限であることに注意してください。 私の意見では、この記事は、データ分析を始めたばかりの人や、理論的には優れているが、仕事のためのツールを選択している人に役立つと思います。