
職場で行われる膨大な数の計算を考慮して、ほとんどの場合、学術環境からの質問を職場でよく聞きます。「同じアプリケーションを起動することと起動することの結果が異なるのはなぜですか。 その中の何も変更しません。」 これについてはすでに会話が行われていましたが、質問には部分的にしか答えていません。 この問題についてもう少しお話しましょう。
同じシステムで次の画像を見ることができるのはなぜですか:
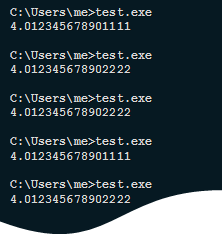
または、次のように、2つの異なるマシンで:

これがすべて起こる主な理由は、数学で常に機能する結合則が、限られたビットグリッドを持つマシンでの計算では実行できないことです。つまり、(a + b)+ cはa +(b + c)
David Goldbergによる記事「すべてのコンピューター科学者が浮動小数点演算について知っておくべきこと」のこのトピックには、多くの興味深いものがあります。 計算で非常に小さい数と比較的大きい数が見つかった場合の簡単な説明例を示します。

数学者として考えれば、すべてが期待されるようです。 ここで、単精度の数値を処理し、小さな数値を大きな数値に追加するとします。

機械計算の観点からは、IEEE 754標準に従って正しい結果が得られ、次の結果も当てはまります。
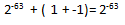
ここからすべての問題が出てきます。 結局、コンパイラーはコードを非常にうまく最適化できるため、式の追加の順序などが変更されます。 そして、 -fp-modelオプションはここで役立ちますが、これについては既に詳しく説明しました。
しかし、すべてがコンパイラに依存するわけではありません。 元の質問は、コード内で何も変更されていないように聞こえたため、「再構成」されていないことを意味しますが、結果は依然として異なります。
そのため、他の要因が登場します。 シリアルアプリケーションおよびパラレルアプリケーションの場合、再現可能な結果を得るための重要な側面の1つは、データのアライメントです。 ところで、パフォーマンスにも大きな影響があります。 そして、コード内のデータを誰も整列させなかった場合、ベクトル化されたループでは、異なる数の反復がプロローグ、ループコア、およびエピローグとして認識され、それに応じて計算の順序が変更されます。 このような問題を防ぐには、次の2つの方法があります。
1)最適化を保存しますが、同時に_mm_malloc()および_mm_free()を使用して、明示的にデータを調整します。 Fortranにはディレクティブがあります!DIR $ ATTRIBUTES ALIGN:64 :: arrayname 、およびコンパイラオプション-align array64byte
2) -fp-model精密オプションを使用して、削減のベクトル化およびその他の最適化を中止します。これにより、パフォーマンスが低下します。
いいね! -fp-model preciseを使用してコードをコンパイルしたが、結果がまだ一貫していないとします。 今何が問題なのですか? 実際、いくつかの理由があります。
まず、アプリケーションが並列の場合、これはスレッドの数です。 OpenMPの削減は、コンパイラオプションの影響を受けません。 したがって、スレッドの数を変更すると、異なるシステムではデフォルトで異なる可能性があるため、削減の追加の順序(およびその数)を暗黙的に変更します。 さらに、スレッドの数が同じでも、OpenMPの小計が開始から開始まで同じ順序で合計されるとは誰も言いません。異なる合計順序、したがって異なる結果を得ることができます。 ところで、これはiccとgccの両方の特徴です。 さらに、結果は、順次バージョンの削減よりも正確である可能性があります。
これを自分で制御する必要があります。バージョン13.0以降のIntelコンパイラには、決定論的な削減を実行できる環境変数があります。 これはKMP_DETERMINISTIC_REDUCTIONです。 yesに設定し、落ち着くことができますが、スレッド間の作業の静的な分散を使用するという条件(静的スケジューリング)で、スレッドの数は変更されません。
Intel Threading Building Blocksを使用する場合、 parallel_deterministic_reduce()関数を呼び出すことにより、そこで削減を制御できます。 ところで、Intel TBBはスレッドの数に依存せず、結果はシリアルバージョンのリダクションと異なる場合があります。
いいね これを追加しましたが、やはり役に立ちません。
次に、「恒常性」に対するあなたの欲求について知らないライブラリが使用されている疑いがあります。 最初に数学関数の呼び出しに注意を払いたいです。 -fp-modelオプションを使用すると、関数呼び出しの一貫性を実現できますが、異なるアーキテクチャ(Intel以外のものを含む)で同じ結果を得るには、 -fimf-arch-consistencyスイッチを使用することをお勧めします。
より「強力な」例は、Intel Math Kernel Libraryの使用です。これは、デフォルトでは再現可能な結果に焦点を合わせていませんが、これは追加の設定を使用して達成でき、いくつかの制限があります。
たとえば、同じスレッド数、静的スケジューラー(OMP_SCHEDULE = static、デフォルトで設定)、同じOSおよびアーキテクチャーで、再現可能な結果を得ることができます。 この機能は、MKL条件付き数値再現性と呼ばれます。 条件付きである理由は理解できると思います。 ちなみに、以前はデータアライメントの要件もありましたが、最新バージョンではエンジニアが「何かに夢中になった」ため、MKLを使用する際にこの状態を処理できなくなりました。 したがって、これらの要件が満たされている場合、環境変数MKL_CBWR_BRANCHを設定(たとえば、値"COMPATIBLE"に設定 )するか、コードで関数mkl_cbwr_set(MKL_CBWR_COMPATIBLE)を呼び出すと、待望の「安定性」が得られます。
したがって、多数の計算を使用する場合、「永続的な」結果を達成することが可能であることを理解する必要がありますが、私たちが述べた多くの条件にのみ従います。 今日のほとんどすべてのツールには、この問題を制御する方法があります。注意して、必要な設定とオプションを設定する必要があります。 よく、まだ-しばしば理由は平凡であり、通常の間違いにあります。 たとえば、初期化されていない変数を使用して、深刻な科学式を計算するコードを見ることは興味深い場合があります。 そして、これが間違った方向に進んだ別のロケットであることに驚いています。 コードを書くときは注意し、適切なツールを使用してコードを作成およびデバッグしてください。
ところで、そんな質問。 Xeonが異なるシステムの例(上の写真)で、異なる結果が得られたのはなぜですか? 私は明らかにそれについて書いていません。あなたのアイデアを聞くのは面白いでしょう。