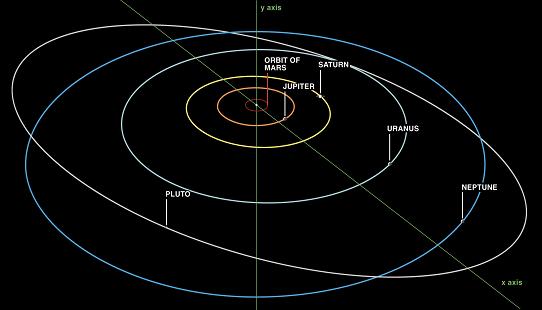
これは何ですか
天体の位置を正確に計算するには、できるだけ多くの妨害要因を考慮する必要があります。 2つを超えるシステムの解析解はありません(例外は特定のラグランジュ解です)。したがって、物体の運動方程式は数値的に解かれますが、比較的新しい数値積分法(エバーハート法など)を考慮しても、この手順は非常にコストがかかり、解が小さい場合に十分に正確です一定の期間は平均的なPCのパワーの下にあるため、グローバルな時間範囲での統合は困難で時間のかかるタスクです。 したがって、問題は次のように解決されました。積分によって天体の位置を見つけ、いくつかの関数によってこれらの位置を近似し、出力でこの関数の係数を取得します。 原則としてエフェメリス理論と呼ばれるのは、これらの係数のセットです。
DE
おそらく、これらは天体の運動の最も一般的な理論です。 この理論の出現は、宇宙技術の発展と、AMSのミッションのための惑星の位置の正確な計算の必要性に関連しています。 今日、この理論のバージョンの膨大なリストがあります。 最も人気のあるものはDE405です。 この理論については、 http : //ssd.jpl.nasa.gov/?planet_eph_exportで読むことができます。
係数は時間ブロックに分割されます。 特定の時代-個々の要因。
これらの係数の式は、 チェビシェフ多項式です。 ところで、チェビシェフ多項式は、天体暦理論を作成するのに最も適したものの1つです。 このような多項式を扱う原理は、O。Montebrookの本-「パーソナルコンピューターでの天文学」( Rutracker.org )に記載されています。
どこで入手できますか?
これらはすべて、NASAのftpサイトにあります。 ASCIIテキスト形式: ftp : //ssd.jpl.nasa.gov/pub/eph/planets/ascii/
おそらく何かコメントがあります。 たとえば、 このフォルダに入力すると、次のようなファイルが表示されます:ascp1600.403、これは1600年の係数であり、理論バージョンはDE403であることが容易に理解できます。
このようなファイルには3つの列があります-それぞれが空間の座標に対応しています。
ただし、これらのファイルのサイズを見ると、作業でそれらを使用することは便利ではないことが明らかになります。 したがって、バイナリバージョンがあります: ftp : //ssd.jpl.nasa.gov/pub/eph/planets/bsp/
申し込み方法
必要なバイナリを入手しましたが、問題は次のとおりです。どうすればよいでしょうか。 幸いなことに、ftpにはさまざまな言語でプログラムを実装する例があります。ftp : //ssd.jpl.nasa.gov/pub/eph/planets/
小さい音
すべての参照は惑星について与えられていますが、理論的には太陽系の小さな物体に対する係数があります。 これはすべて同様に次の場所にあります: ftp : //ssd.jpl.nasa.gov/pub/eph/
VSOP 87
もちろん、この理論は以前の理論ほど一般的ではありませんが、初心者にはお勧めできます。 この理論には主な欠点があります-それは惑星と太陽だけの位置を説明します。 この理論の式の形式は、三角級数です。
どこで入手できますか?
シンプルでシンプルです。ウェブサイトhttp://www.neoprogrammics.com/vsop87/source_code_generator_tool/にアクセスし 、設定で目的の言語とデータ形式を選択するだけです。
この天体暦の主な利点は、準備が簡単であることです。
既製のコードがあれば、私たちの多くはすでにそれで何かをすることができると思います。 ただし、まだ少しヒントが必要な場合は、 こちらからお問い合わせください。
EPM
この天体暦理論への参照はほとんどありません。 ロシア科学アカデミーの応用天文学研究所で作成されました。 この理論には3つのバージョンがあり、それぞれEPM 2004、EPM 2008、EPM 2011です。
どこで入手できますか?
ソースはftp IPA RASにあります:ftp: //quasar.ipa.nw.ru/incoming/EPM/Data/ 。 フォルダの名前は、理論バージョンに対応しています。 DEで実装されているように、各理論にはそれぞれバイナリファイルとテキストファイルがあります。 また、ここでもテキストファイルの重量が非常に大きいため、バイナリを使用する必要があります。
申し込み方法
実装するのが最も難しいと思われるのは、この理論です。 それにもかかわらず、その開発者は私たちの世話をし、異なる言語でいくつかの例を与えました: ftp : //quasar.ipa.nw.ru/incoming/EPM/ 。
理論自体はチェビシェフ多項式に基づいて構築されており、 ここでも非常によく説明されています 。
精密ノート
すべての理論が最も正確ではないことに注意してください。 上記の中で最も精度が低いのはVSOP87です。 DEとEPMはかなり正確です。後者は相対論的効果を考慮に入れることに注意する価値があります。 ただし、これまでに解決したほとんどすべての適用タスクにVSOP 87を使用しましたが、実際には、その精度は不十分ですが、それでも基本的な観測と比較すると目立ちません(10分の1または100分の1の偏差がある場合があります)角度の秒)。
結論として
EPMの理論に関して、もう少しお話しします。 私は個人的な会話からこの理論について学びましたが、それはかなり狭いサークルで知られており、それを使用するユーザーはほとんどいません。明らかに、これはこの理論を広いサークルに広めることに対する研究所の無関心と何らかの関係があります。他の理論との関係で競争力があります。