1.ローレンツアトラクタについて

エドワード・ノートン・ローレンツ(1917-2008)は、今日の科学で非常に人気のあるカオス理論の創始者です。 彼は、米国ニューハンプシャー州のダートマス大学とケンブリッジのハーバード大学に通っていました。 第二次世界大戦中、彼は米陸軍の航空隊で気象学者を務め、その後、マサチューセッツ工科大学で教授として働いていました。
1963年、彼の記事「確定的非周期的フロー」がJournal of the Atmospheric Sciencesに掲載されました(ロシア語訳:E. Lorenz。確定的非周期的フロー//ストレンジアトラクター。-M。:Mir、1981、p。88-117)、カオス理論の基礎を築いただけでなく、気象現象のモデリングの考え方も変えました。 この研究では、初めて、3次常微分方程式の非線形自律システム(動的システム)がナビエ・ストークス方程式系から得られました。二次高調波:
(1)
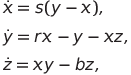
ここで、 s 、 r 、およびbはいくつかの正の数、システムパラメーターです。 通常、ローレンツシステムの研究は、 s = 10 、 r = 28、およびb = 8/3 (古典的なパラメーター値)で実行されます。
一般に、カオス理論は、決定論的な力学系の挙動を研究する数学の分野であり、解はかなり複雑な構造を持っているため、やがてランダムに挙動すると思われます。 決定論的システムとは、運動方程式があり、そのパラメーターと初期条件が既知であり、ランダムではないシステムです(Moon F. Chaoticoscilations。-M。:Mir、1990)。
動的システム(1)は、他のプロセスでも発生します。
1.トロイダルチューブ内の対流(Landa PS非線形振動と波。-M:LIBROKOM、2010、pp。454-455);
2.シングルモードレーザー(LA Pokrovsky。大きなレイリー数の漸近極限におけるローレンツ方程式系の解。I。最も単純な量子レーザーモデルのローレンツ系とそれに平均化法の適用// Theoretical and Mathematical Physics、1985、v。62、No. 2、p。272-290);
3.慣性励起を伴う発振器(Neymark Yu.I.、Landa PS確率的およびカオス的振動-M:LIBROKOM、2009、p。288-295)。
ローレンツシステムの任意のソリューションでは、対応する位相軌道が固定半径の球に永久に浸る瞬間が存在します。 したがって、ダイナミカルシステムのすべての軌跡が引き付けられる制限セット(ローレンツアトラクタ)が存在します。
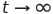 (Nemytsky V.V.、Stepanov V.V.微分方程式の定性理論。-M .: URSS社説、2004年、357-359ページ)。 したがって、アトラクタはシステム(1)のソリューションの動作を長期間にわたって決定します。
(Nemytsky V.V.、Stepanov V.V.微分方程式の定性理論。-M .: URSS社説、2004年、357-359ページ)。 したがって、アトラクタはシステム(1)のソリューションの動作を長期間にわたって決定します。
一般的な形式の非線形動的システムを解くための正確な方法がないため、たとえば、明示的なオイラースキームと中央差分スキーム、アダムス、高次導関数の使用、およびルンゲクッタ4番目の組み合わせなど、数値メソッドを使用してアトラクターの構造を分析することがよくあります注文。 システムパラメータの古典的な値の場合、システムの平衡位置はaddle型であるため、その解の不安定性が観察されます。 積分間隔が長くなると一般的な誤差が大きくなるため、これらの方法の適用が制限されます。 したがって、システム(1)(つまり、大気)の初期条件の小さな変化は、時間の経過とともに重大な結果につながる可能性があります。
70年代に。 20世紀には、数値実験の結果に基づいたHookenheimer、Williams、Yorkは、ローレンツアトラクターの構造に関する仮説をシステムパラメーターの古典的な値で定式化しましたが、この仮説とシステムの誘引セットの構造(1)との対応は厳密には証明されていません。 2000年に、スティーブンスメールは21世紀の18の最も重要な数学的問題のリストを編集しました。 ローレンツアトラクターの構造の問題は、このリストの14番に含まれていました。2002年に区間演算を使用してワーウィックタッカーによって解決されたと考えられていますが、多くの数学者は、システム(1)。
パラメーターの古典的な値を持つローレンツ系の数値研究に関する文献では、計算実験から得られたデータに基づいてアトラクターの構造について結論が下されることがよくあります(たとえば、アトラクターにはサイクルが含まれます)。 ただし、ステップを選択する正当な理由はなく、どの種類の実数を使用する必要があり、どの期間に計算が行われたのかがわかりません。
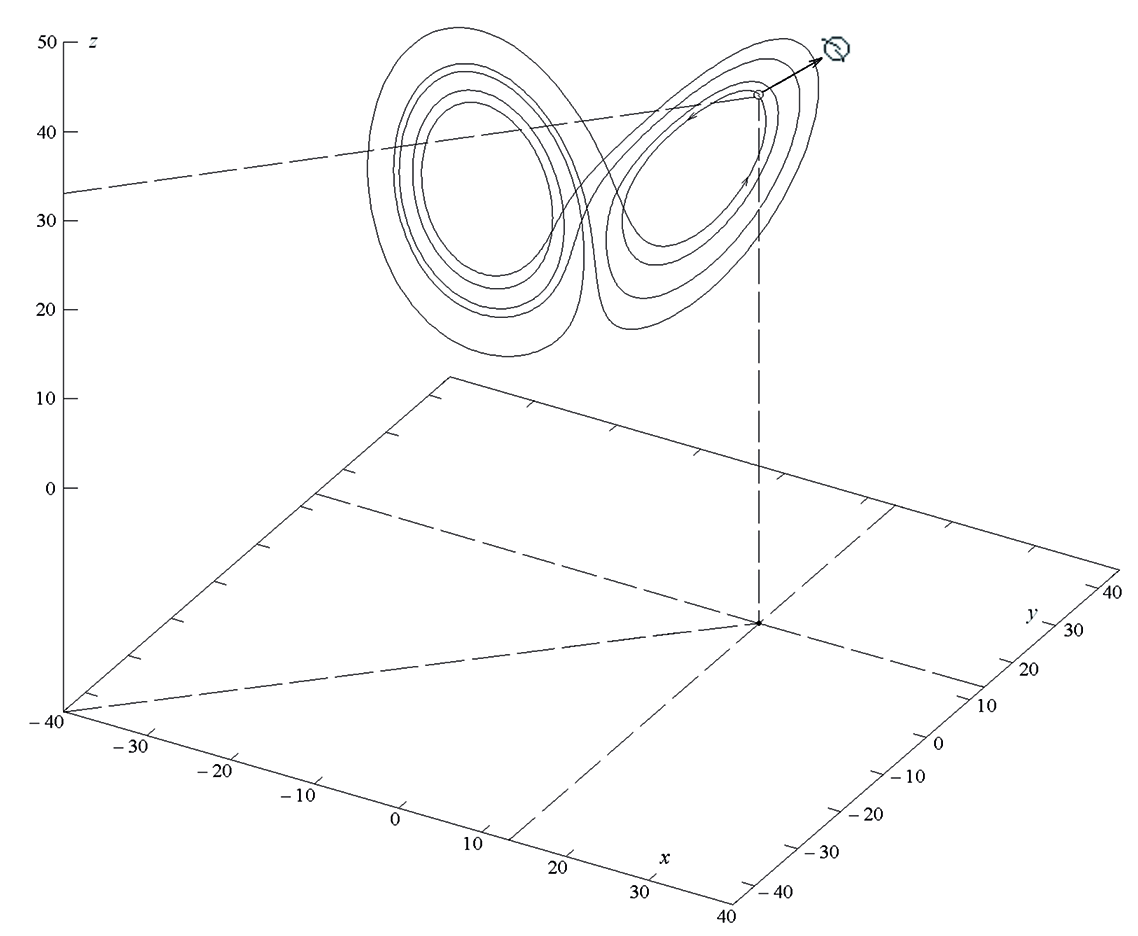
図 1. x(0)= 13.41265629、y(0)= 13.46430003、z(0)= 33.46156416の時間間隔[0; 6.827]で構築された軌跡の弧。
ビルコフの定理(ネミツキーVV、ステファノフVV微分方程式の定性的理論。-M .: URSS論説、2004年、402ページ)により、ローレンツアトラクターは回帰軌道を含み、各回帰運動はポアソン安定です。 これは、瞬間の任意の大きな値があること、つまりシステムの軌道のポイントがその初期位置の任意の近傍にあることを意味します。 サイクルもそのような反復運動である可能性がありますが、初期条件の特定の近傍への軌道の見つかった戻りに基づいてこれを結論付けることは不可能です。 計算が示したように(図1)、ローレンツシステムでは、アトラクター上の解の振る舞いのダイナミクスは非常に複雑です-その中に含まれる再帰的な軌道は、例えば、ほぼ周期的な解によって記述されるか、より複雑な構造を持つことができます。 このようなソリューションの動作を備えた非自律システムの例を作成しました 。
2.ローレンツシステムのダイナミクスのモデリング
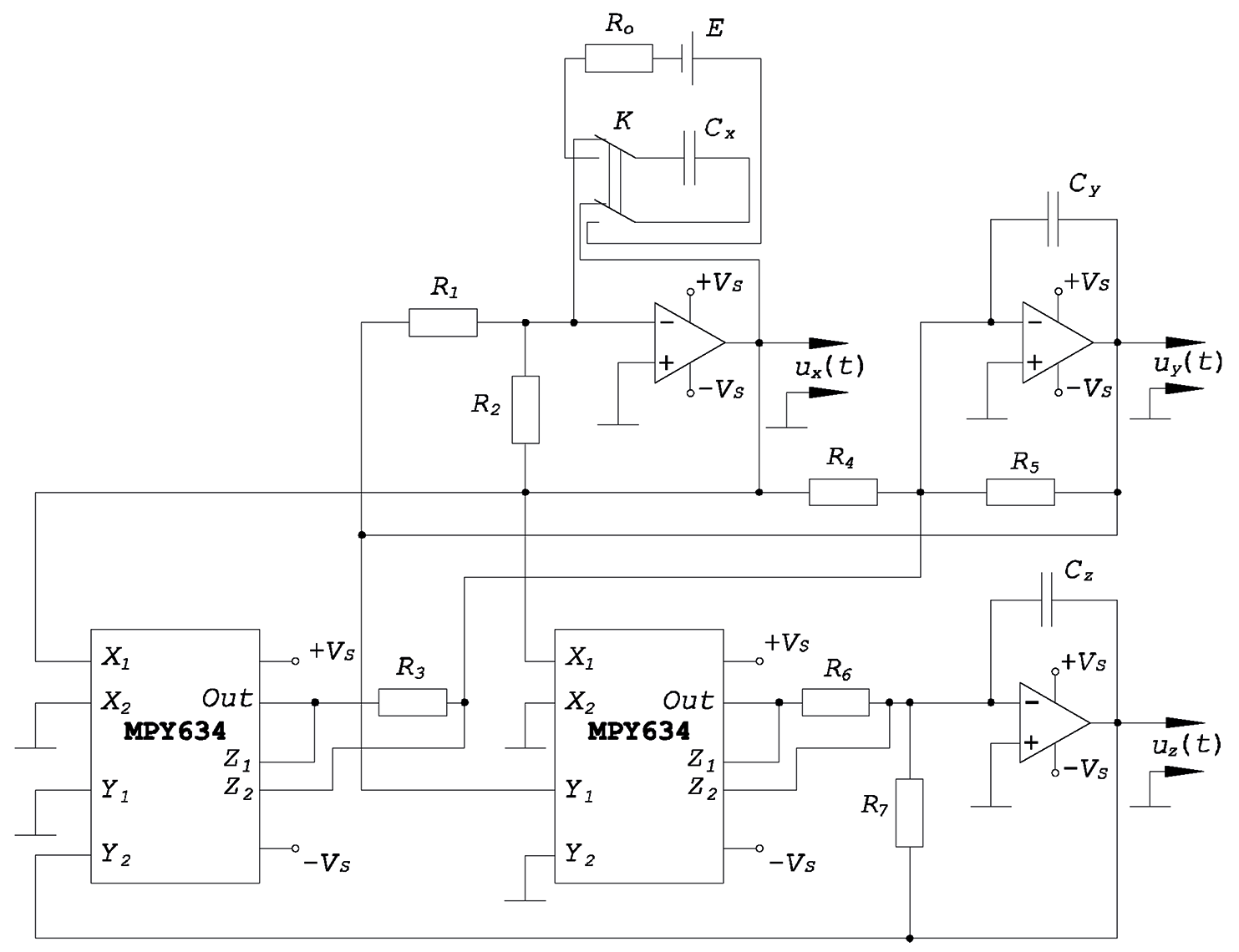
図 2.ローレンツシステムのダイナミクスを記述する振動発生器のスキーム。
右側の特定のタイプの非線形性を持つ動的システムのアトラクタ上の軌跡を記述する信号(カオス振動)を生成するために、実際には電気回路/またはアナログコンピューター/(Dmitriev A.S.、Panas A.I. Dynamic。 chaos:通信システム用の新しい情報キャリア-M .: Fizmatlit、2002)。
図に示されている発振発生器の電気回路を考えてみましょう。 2、数値モデリングの代替として。 ローレンツシステムは3次であるため、回路の電圧変化のダイナミクスを作成するには、ノイズの問題が微分器に関連するため、オペアンプに基づく3つの積分器が必要です。 この場合、回路を構築して積分方程式を書くには、図6に示す最新のアナログ乗算器MPY634を含む基本回路を使用します。 チップメーカーの公式ドキュメントの 3。 私たちが持っています:
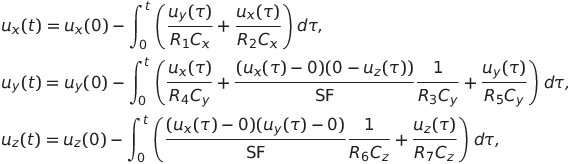
どこで
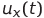 、
、 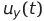 そして
そして 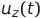 -関数x ( t ) 、 y ( t )およびz ( t )に対応する瞬間応力値(これらの電圧のペアは、オシロスコープのプレートに適用できます-結果の複雑な図は、対応する平面上のローレンツシステムの軌跡の投影です)、
-関数x ( t ) 、 y ( t )およびz ( t )に対応する瞬間応力値(これらの電圧のペアは、オシロスコープのプレートに適用できます-結果の複雑な図は、対応する平面上のローレンツシステムの軌跡の投影です)、  そして
そして 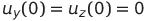 -コンデンサ両端の初期電圧
-コンデンサ両端の初期電圧 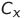 、
、 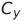 そして
そして 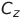 したがって、 SF = 10 Vは乗数のスケール係数です。
したがって、 SF = 10 Vは乗数のスケール係数です。
コンデンサは最初に充電されます
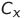 電源Eから。 抵抗器
電源Eから。 抵抗器 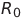 再充電を目的としています( Kキーの状態は、発電機回路の図に示されています)。 残りのコンデンサの初期充電はゼロです。 基本的に、システム(1)の初期条件を設定します。 初期充電回路は、次の場合を除いて変更できます(たとえば、2つのコンデンサの充電)。
再充電を目的としています( Kキーの状態は、発電機回路の図に示されています)。 残りのコンデンサの初期充電はゼロです。 基本的に、システム(1)の初期条件を設定します。 初期充電回路は、次の場合を除いて変更できます(たとえば、2つのコンデンサの充電)。 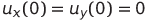 。 これは
。 これは 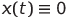 、
、 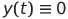 そして
そして  システム(1)の特定のソリューションです。
システム(1)の特定のソリューションです。 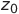 任意の定数です。 この場合、ためらわないことは明らかです。
任意の定数です。 この場合、ためらわないことは明らかです。
交換する
 各積分方程式の両方の部分を時間で区別します。 ゲット
各積分方程式の両方の部分を時間で区別します。 ゲット
(2)

システムのパラメーターの古典的な値でダイナミクスをシミュレートします(1)。 抵抗と容量の値を等しく設定します
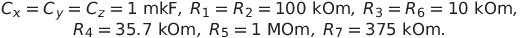
次に、システム(2)は次の形式を取ります。
(3)

(3)の変更
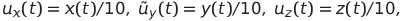
ローレンツシステムを取得します。 以来
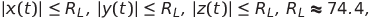
次に、導入された代替品から、電圧の絶対値が7.44 Vを超えないことがわかります。これは、 MPY634乗算器のドキュメントで提供されています。 Eの値は、 1.5 V (指型バッテリーのEMF)に等しく選択できます。
提示されたモデルの精度は、実際の静電容量と抵抗の誤差、および積分器と乗算器の周波数特性によって決まります。
PS
最近、数学の会議でこのトピックについて報告しました。 こちらで見ることができます (ビデオの品質については事前に謝罪します)。 また、そこからレポート資料をダウンロードすることもできます(ビデオの品質のためにプレゼンテーションがはっきりと表示されないため、レポートと同期してプレゼンテーションを表示することをお勧めします)。