-彼らにはたくさんの詩人がいます。 誰もが詩を書き、すべての詩人は、
当然のことながら読者がいます。 読者は生き物です。
組織化されていない、彼はこの単純なことを理解していません。 彼は幸せです
良い詩を読んで覚えさえするが、悪いものは知らない
欲望。 不公平、不平等、そして
そこに住む住民はとても繊細で、誰もが気分が良くなるように努力しています
特別な職業-読者。 一部はアンビックに特化しており、他は舞踏病に特化しており、コンスタンチン・コンスタンティノヴィッチは両親媒性および
現在、アレクサンドリアの詩を習得し、2番目の専門分野を取得しています。
このワークショップは当然、有害であり、読者は強化するだけでなく
食べ物だけでなく、短期休暇も頻繁にあります。
ストルガツキー、三人の物語
私はこの質問に興味がありました。誰もが「詩人」であり読者である状況で誰もが読み始める才能のある「詩人」の人気の高まりは、正確にどのくらいですか。 「詩人」という言葉を引用したのは、実際には、エピグラフに記載されているものはすべて、現在のブロゴスフィアとソーシャルネットワークに似ているからです。
この投稿では、多くの数式、グラフ、およびすべての疑似科学的なボルト論があります。 モンテカルロ法を使用してJavaScriptを使用して小規模なソーシャルネットワークをモデル化する例を示します。 私は究極の真実のふりをしません。 ただし、この投稿は、自分自身に似たようなことをしたい人には役立つと思われます。
したがって、まず、非常に単純化された仮想「ブロゴスフィア」の機能について説明します。
1. N人の参加者があり、それぞれが番号i = 1 ... Nで特徴付けられます。
2.それぞれが他の参加者(友人)のK個を読み取ります。 これはすべて、2次元配列によって定義されます。
P i、kには、 i番目の参加者のk番目の友人の番号が含まれます。
3.参加者ごとに、 ハットピースがランダムに選択されます(すべて同じ)「敵」-この参加者が自分自身を決してendさない参加者の数。
4.各参加者iには個人の財産、つまり才能の尺度があります。 配列T iに格納されます。
5. T iの値は、最初から各参加者にランダムに分配されます。
6.また、最初に、各参加者はランダムな友人のK個を受け取ります。
7.さらに、各R iの読者の数はすでにランダムであり、少なくともKの値にほぼ近い(全員がKのランダムな人を読む場合、彼自身もほぼ同じように読まれます)。
8.実験の日数が設定されます。
9.正の数qおよびrが設定されます。qは、投稿の質が参加者にとってどれほど重要であるかを特徴づけ、 rは、フレーディングを決定する際に既存の人気がどれほど重要かを特徴づけます。
日ごとに、メインループの1つの反復を意味します。 このサイクルで何が起こるか。
1.各i参加者が1つのQ i品質の投稿を書き込みます。 Q iの値はランダム変数ですが、その分布は才能T iに依存します。 T iの値が高いほど、参加者iからの質の高いQ iの投稿が表示される可能性が高くなります。
2.各参加者iについて、最後の3つの投稿の品質が他の友人の品質よりも低い1人の友人が選択されます。 この友人を新しい友人と交換します。
3.友人の友人の中から代替候補を探し、すでに友人または敵である人々を除外します。
4.置換候補リストのそれぞれに、選択する確率を特徴付ける番号を割り当てます。 この確率は、彼の最後の3つの投稿Q iの品質と、 R iの既存の人気度に依存します。 私のモデルの確率は、簡単な式で記述されます:
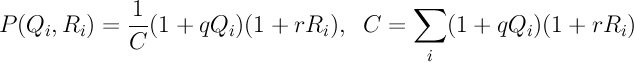
ご覧のとおり、候補者の投稿が優れていて人気が高いほど、候補者を選択する可能性が高くなります。 すべての志願者に同じ定数Cは正規化に役立ち、すべての候補者のすべての確率の合計が1に等しくなります。
5.ランダムに、ただし不均等な確率を考慮して、準備されたリストから置換を選択し、古い友人を新しいものに置き換えます。 そして、 Nのそれぞれについても同様です。
この研究で興味深い主な指標は、読者数R i 、それが毎日どのように変化するかです。 具体的には、最も才能のある最初の3人の参加者。
6.すべての置換の後、分布R iの分散値Dを計算します。 数値Dは、平均読者数からの標準偏差を示します。 たとえば、 Nのそれぞれに同じ数のリーダーがある場合、平均はこの数に正確に等しくなりますが、平均からの偏差はありません(すべて同じです!)、分散はゼロです。 しかし、読者の数の不平等が大きければ大きいほど、 Dの分散は大きくなります。 彼女の表現は次のとおりです。
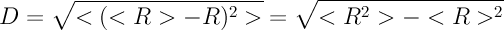
山括弧は、すべての参加者の平均を示します。
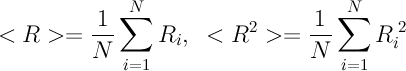
7.グラフにさらに出力するために必要な統計が配列に記録され、日が経過するまでサイクルが繰り返されます。
また、シミュレーションの一環として、このような実験が行われます。 DayXの普通のメンバー(うさぎ)の1人が、突然、最も才能のある参加者+ 1人の読者と同じ才能を手に入れました。 それでは、 DayXの時点ですでに才能が読者の最大数を獲得していることを考えれば、彼はどのようにして名声の頂点に立つのでしょうか? 彼の成功も監視されています。
詳細に入ります。 モンテカルロ法のタスクの1つは、与えられた分布で乱数を生成することです。
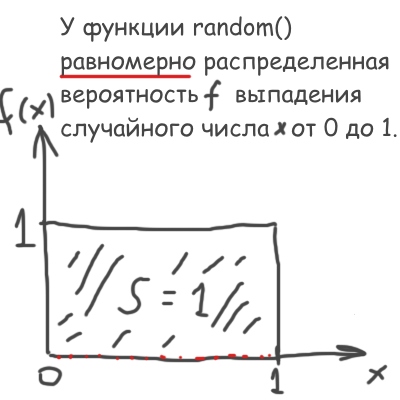
つまり、標準のマシン関数から独自の特別なものをランダムに作成する必要があります()均一な分布(上記の図):
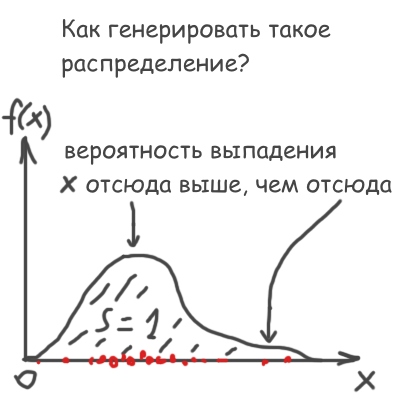
f(x)dxの値は 、定義により、 xからx + dxの区間にある数の確率に等しいことを思い出させてください。 したがって、それ自体では、 f(x)の積分は1に等しくなければなりません。
いくつかの特別な形式f(x)では、問題は分析的に解決されます。 そこで、ランダムなTタレントを生成するために、フェージング指数を使用しました。
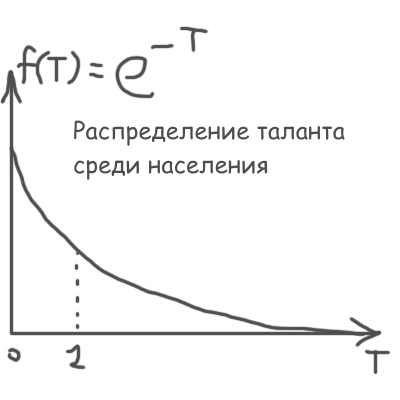
まったく同じ指数を使用して、特定の才能Tを持つ参加者のランダムな品質のQ投稿をさらに生成しました。

では、0から1まで一様に分布した乱数Rndを使用して、上図に示されている法則f(x)に従って分布したQを生成する方法は? 非常にシンプル:
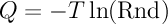 。
。
さて、最大の分散とは何か、なぜ「敵」が導入されるのかについて。
反感のない最初のバージョンでは、状況は単純に発展しました。N人の参加者全員のK人の友人のリストは同じで、最も才能のある最初のK人が含まれていました。 まあ、 K + 1には、それらのKファーストを犠牲にして読者がいました。 この状況は分散Dの最大値に対応し、これはほぼ等しい(条件1 << K << Nの場合):
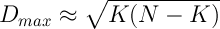 。
。
導入する「敵」が多いほど、結果の分散は小さくなります。 したがって、シミュレーション結果は次のとおりです。
人々が投稿の品質よりも人気を重視する場合:
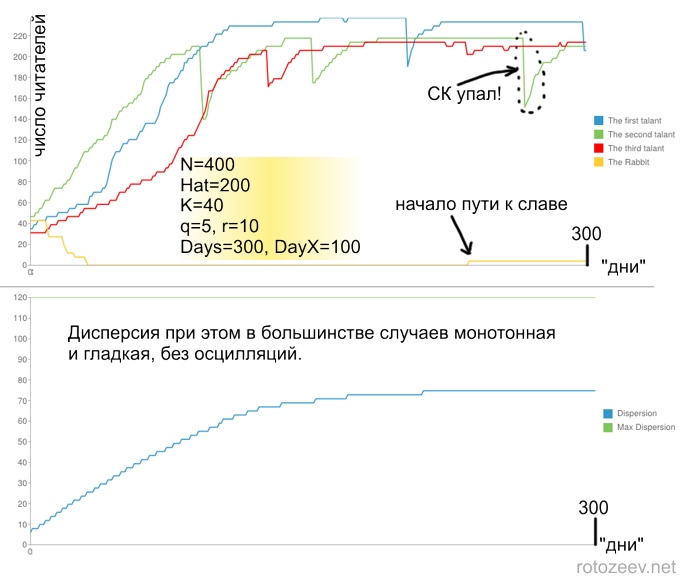
ほとんどの場合、人気を得るのは遅いです。 人気に一時的な失敗があります(これはLiveJournalで定期的に投稿を作成する人に対する考えられる答えです。 これは、選択された配信機能の特性によるものです。才能がある場合、ほとんどの投稿はゼロに近い傾向があります。
人々が投稿の人気と品質を等しく評価している場合:
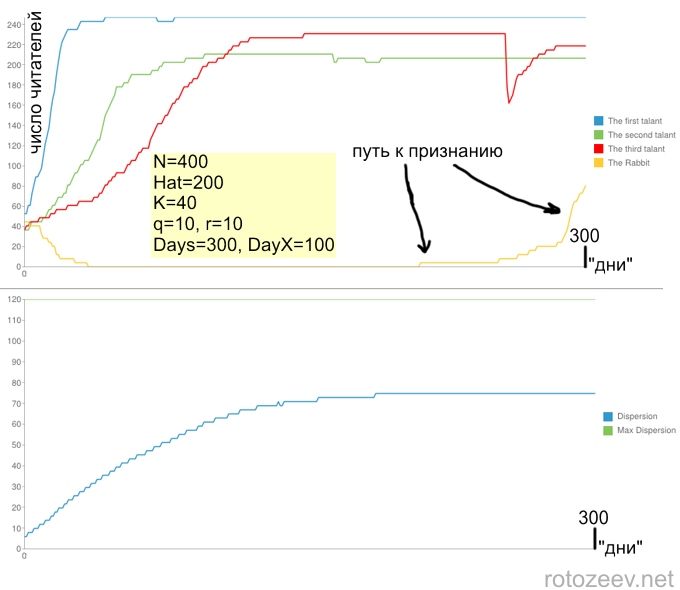
同じパラメータを使用したアルゴリズムのさまざまな実装により、時間に応じてリーダーの数が非常に多様に依存することに注意してください。 一般的な機能はありますが、非常にあいまいです。 ただし、積分の平均値としての分散の依存性は、同じパラメーターに対して実質的に変化しません。 分散対時間に応じて、2つのパラメーターが重要です:漸近線に到達する時間、つまりブロゴスフィアが平衡状態になり、その後に読者のマスフローが発生しなくなる時間、およびNとHatの比率によって決定される漸近的な時間です。
アルゴリズムはJavaScriptで実装され、グラフィックはChart Google APIを使用して描画されたため、現代のコンピューターのユーザーはこれらの結果を簡単に再現したり、実装を改善したりできます。
将来のための小さな楽しい(簡単なため)質問:セットN全体ではなく、ランダムに選択された参加者の少数n << Nを平均すると、分布R iの分散がどのくらい正確に計算されますか? 確かに、小さなランダムなサンプルがブロガーの全人口をよく反映していることが判明した場合、たとえば、同じLJの「天気」を監視できます-毎日分散を計算し、その傾向を評価します。