ところで、 21世紀のアインシュタインはアルバートとも呼ばれると信じている人もいます 。 つまり、アルバート・バラバシ。
他人の作品を尊重する人にとって、翻訳は著作権であり、引用や言及には元の翻訳へのリンクが必要であることを思い出します。 他の人の仕事を尊重しない人が、この記事で議論されることを気にしないことを願っています。
翻訳では、 重要な結論と翻訳の著者によって強調された記事で与えられた基本概念が太字で強調されます。 翻訳の著者のコメント、 定義へのリンク、および記事に記載されているいくつかの概念と方法に関する追加情報は 、斜体で強調表示されます。
複雑なネットワークを管理する
自然で人工的なシステムを完全に理解しているという証拠は、これらのシステムを制御する能力にすぎません。 制御理論は、工学システムと自然システムを管理してそれらを望ましい状態にするための数学ツールを提供するという事実にもかかわらず、複雑な自己組織化システムを管理するための単一のインフラストラクチャはありません。 この記事では、システム全体のダイナミクスを意図的に制御できる時間依存制御を使用してドライバーノードのセットを決定するだけでなく、任意の複合指向ネットワークの制御性を研究するための分析ツールを開発します。 これらのツールをいくつかの実際のネットワークに適用し、ドライバーノードの数がネットワークの次数分布によって主に決定されることを確立しました。 多くの実際の複雑なシステムに現れる異種の異種ネットワークを制御することは最も困難であり、わずかなドライバーノードで高密度および同種のネットワークを制御できることを示します。 逆説的に、モデルおよび実際のシステムのように、ドライバーノードは、通常、高度のノード （次数ノード、 入力または出力接続の数）を 持たないことがわかりました。
制御理論の原理によれば、動的システムは、入力変数の特定のセットについて、 1〜3の有限時間で任意の初期状態から任意の状態に移行できる場合に制御可能です。 この定義は、制御の直感的な理解と一致しており、ペダルとステアリングホイールを操作することにより、ドライバーが目的の速度で所定の方向に移動する方法と同様に、いくつかの入力変数を適切に操作することでシステムを目的の状態にすることができます。 制御理論は、電気回路、生産プロセス、通信システム4-6 、航空機、宇宙船、ロボット2-3に適用される数学的に高度に開発された技術分野であるにもかかわらず、自然界で発生する複雑なシステムの制御性に関する基本的な問題とテクニックには解決が困難です。 難点は、それぞれ独自のレベルの不確実性を持つ2つの独立した要因を管理する必要があることです。
（1）システムのアーキテクチャ。どのコンポーネントが相互作用するかをカプセル化したネットワークで表されます。
（2）コンポーネント間の時間依存の相互作用をキャプチャする動的ルール。
したがって、進歩は 、同期ネットワーク7-10 、小さな生体回路、および通信ネットワーク4-6の速度制御の管理など、 両方の層が十分に描写されているシステムでのみ可能です 。 複雑なネットワークの定性的なトポロジ特性を定量的な12-16に減らす最近の進歩により、要因（1）が明らかになり、一部のネットワークは他のネットワークよりも制御が容易であり、ネットワークトポロジがシステムの制御性にどのように影響するかがわかります。 概念的に革新的な作業17-23 （ 追加情報のセクションIIを参照）にもかかわらず、複雑なシステムで最も頻繁に発生する大規模で重みのある有向ネットワークに関するこれらの質問に対する主な回答がまだありません。
ネットワーク管理性
実際のシステムの大部分は非線形プロセスに基づいていますが、非線形システムの可制御性は、多くの点で線形システム3の可制御性と構造的に類似しています。
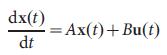（1）
ここで、ベクトルX（t）=（X1（t）、...、Xn（t））は、時間tでN個のノードで構成されるシステムの状態を修正します。 例えば、Ｘ（ｔ）は、通信ネットワーク２４内のノードｉを通過するトラフィックの量、または遺伝子調節ネットワーク ２５内の転写因子の濃度を示し得る。 次元NxNのマトリックスAは、システム接続図と、コンポーネント間の相互作用力（たとえば、個別の通信回線上のトラフィックまたは規制相互作用力）を示します。 最後に、Bは次元MxN（M <= N）の入力行列であり、外部コントローラーによって制御されるノードを識別します。 システムは、コントローラー（図1a）によって導入される時間tに応じて、入力ベクトルU（t）=（U1（t）、...、Um（t））によって制御されます。 Ui（t）は複数のノードを制御できます。
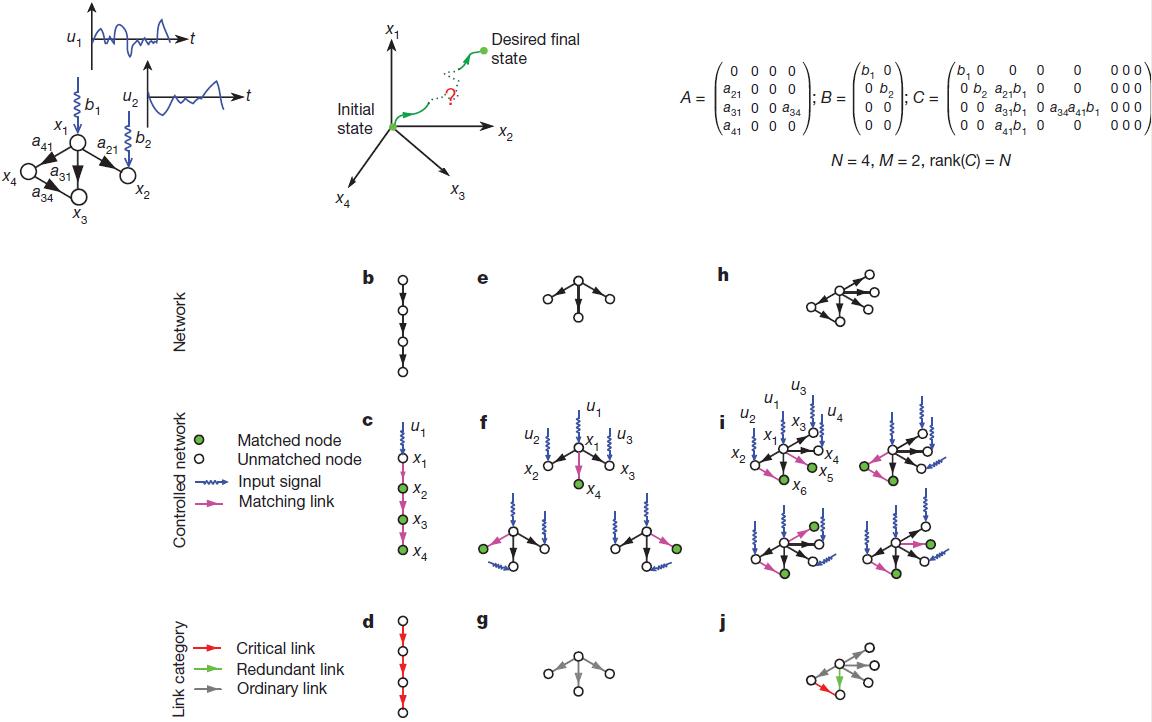
図1 | シンプルなネットワーク管理。 a、小さなネットワークは入力ベクトルによって制御できます
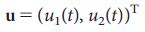（左）。これにより、ネットワークを初期状態から状態空間内の目的の最終状態に移動できます（右）。 方程式（2）は、行列（C）の可制御性を提供します。この場合、システムは可制御であることを示すフルランクです。 b、シンプルなネットワークモデル：指向軌道。 c、指向軌道の最大マッチング 。 飽和した結合は紫色で、飽和したノードは緑色で、緩いノードは白色で表示されます。 ノードの一意の最大一致にはすべてのリンクが含まれるため、それらのいずれも開始ノードでも終了ノードでもありません。 最上位ノードのみがフリーであるため、それを制御すると、指向軌道を完全に制御できます（ 
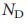= 1）。 d、図bに示す方向パスでは、すべてのリンクが重要です。つまり、リンクを削除すると、ネットワークを制御する能力が失われます。 e、小規模ネットワークモデル：指向性スター。 f 、指向性スターの最大一致。 最大マッチングの一部にできるリンクは1つだけで、3つの空きノード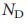（ = 3）。 3つの異なる最大一致は、3つの異なるノード構成が完全に制御できることを示しています。 g、オリエンテッドスターでは、すべての接続は通常です。つまり、それらを削除すると一部の制御構成が奪われる可能性がありますが、ネットワークは同じ数のドライバーノードで管理できます。 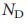。 h、小規模ネットワークの例。 i、 2つの接続のみがネットワークhの最大一致の一部になり、4つの空きノード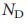（ = 4）。 このネットワークには4つの異なる最大マッチングがあります。 j、ネットワークには1つのクリティカルリンク、1つの冗長リンク（制御構成を失うことなく削除できる）、および4つの通常のリンクがあります。
システムを制御する場合は、まずノードのセットを決定し、 さまざまな信号を使用してノードのセットを制御する必要があります。これにより、ネットワークを完全に制御できます。 これらのノードをドライバーと呼びます。 システムのダイナミクスを完全に制御するのに十分なドライバーの最小数を決定することは特に興味深いです。 Ndで示します。
方程式（1）で記述されたシステムは、有限時間内に任意の初期状態から任意の最終状態に移行できる場合、制御可能と呼ばれます。
（2）次元N x NM、フルランク 
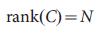（3）
この方程式は、システムの可制御性の数学的条件であり、 ランク 1.2 （図1a） によるカルマン可制御性基準と呼ばれます。 実用的な意味では、次のように制御可能性を考慮して、式（3）が満たされるような最小数のドライバーノードを決定することもできます。 したがって、たとえば、式（3）は、図1のノードx1に対する制御を示唆しています。 ノードx1、x2、x3、およびx4の状態は信号u1（t）によって一意に決定されるため（図1c）、入力信号u1を使用する1bはシステムを完全に制御します。 同時に、反対に、図の上のノードへの影響 1eは完全な制御には十分ではありません。
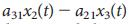（ここでaijは行列Aの要素です）u1（t）を使用して一意に決定することはできません（図1fおよび追加情報のセクションIII.Aを参照）。 完全に制御するには、ノードx1と{x2、x3、x4}の2つの他のノードを同時に制御する必要があります（より複雑な例については、図1h、iを参照してください）。
方程式（2）および（3）を任意のネットワークに適用するには、各接続の重み（つまり、aij）を知る必要があります。これは、ほとんどの実際のネットワークでは未知（例：規制ネットワーク）であるか、またはおおよそ既知であり、時間に依存します（例：インターネットトラフィック）。 すべての重みがわかっていても、 ブルートフォース検索では、行列Cのランクを計算する必要があります。
さまざまな組み合わせ。これは、大規模なネットワークでは過度に計算が困難なタスクです。 リンクの重みを測定する必要性を回避するために、システムが式（3）を満たすようにAとBで非ゼロの重みを選択できる場合 、 システム（A、B）は「構造的に制御されます」 26 。 構造的に制御されたシステムは、システムのパラメーターがいくつかのランダムな制約を満たしたときに発生するゼロ測定を伴ういくつかの病理学的ケースを除いて、重み係数のほぼすべての組み合わせで制御できます26、27 。 したがって、構造制御可能性は、Aの結合重量に関する不完全な知識を本質的に克服するのに役立ちます。さらに、構造制御可能性は線形化されたシステム28の連続体の制御可能性を意味するため、ほとんどの非線形システム3 （セクションIII.A 追加情報 ）。
ドライバーノードのブルートフォース検索を回避するために、ネットワークの完全な制御を維持するために必要な入力またはドライバーノードの最小数は、ネットワークの「最大一致」、つまり開始ノードまたは終了ノードを含まない接続の最大セットによって決定されることを証明しました（図1 c、f、i）。 接続が最大一致のポイントを指す場合、ノードは飽和状態と呼ばれます。そうでない場合、ノードは空き状態です。 補足情報で示したように、構造制御可能性の問題はネットワーク内の同等の幾何学的問題に対応します。各自由ノードを直接制御し、すべての飽和ノードの入力信号からの方向パスがある場合にのみ、指向ネットワークを完全に制御できます29 決定する能力
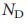、このマッピングを使用することが最初の主要な結果です。 指向性ネットワークの最大マッチングは、以下のステップ数で数値的に決定できるため、 
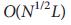ここで、Lはリンクの数を示します。マッピングは、任意の指向性ネットワークのドライバーノードを決定するための効率的な方法を提供します。
実際のネットワークの管理性
以前に開発したツールを使用して、いくつかの実際のネットワークの管理性を調査しました。 ネットワークはその多様性のために選択されました：たとえば、調節の遺伝子ネットワークの目標は細胞プロセスのダイナミクスを制御することであるため、結果は制御の観点から効果的であり、理論的には少数のドライバーノード（すなわち、小さい
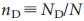） それどころか、これはWorld Wide Webまたは引用ネットワークの管理容易性には期待されないため、この質問を評価することさえ難しくしています。 
。 最後に、管理に対する認識（または抵抗）に対する中立性を考慮したソーシャルネットワークには、高い信頼性が必要であると主張できます。 、システム全体を制御するために、ほとんどの人を個別に制御する必要があるためです。 ドライバーノードの最小セットを決定するために、最大一致へのマッピングを使用しました 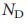表1のネットワークの場合。得られたデータは私たちの期待と矛盾しています。グループとして、遺伝子調節ネットワークは高い （0.8）、ノードを完全に制御するには約80％のノードを独立して制御する必要があることを示しています。 それどころか、一部のソーシャルネットワークは最小値によって特徴付けられます。 、原則として、複数の人がシステム全体を制御できることを示唆しています。
表1 | この記事で分析された実際のネットワークの特性
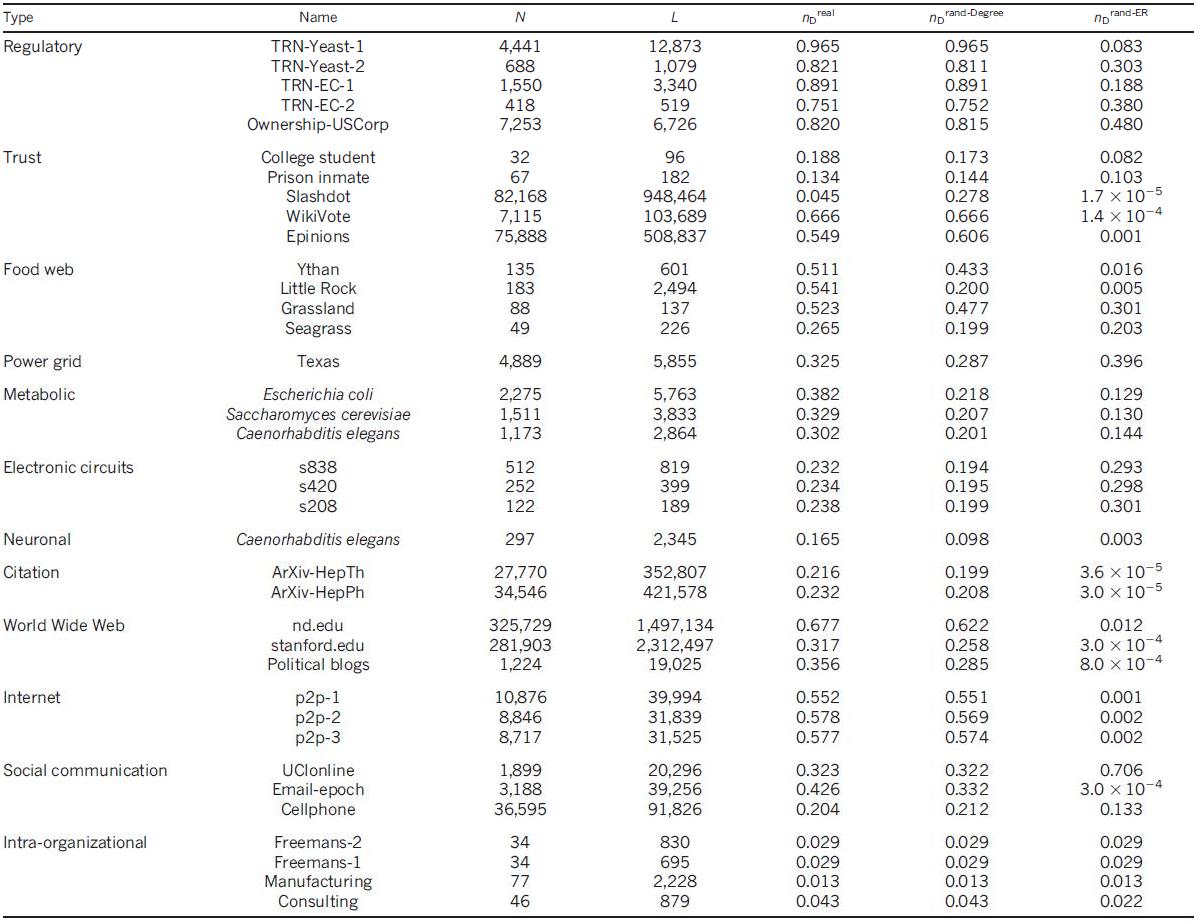
ネットワークごとに、そのタイプと名前が示されています。 ノード数（N）および結合数（L）; 実際のネットワークで計算されたドライバーノードの密度
、次数の保存によるランダム化後 
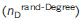そして完全なランダム化の後 
。 データソースおよびリンクへのアクセスについては、 追加情報のセクションVIを参照してください。
ハブ（高度のノード）が32.33の伝搬現象および8.34の同期における31.32の中断および外部の影響からネットワークの構造的整合性を維持する上で重要な役割を担っていることを考えると、ハブの制御が必要であると仮定するのは自然でしょうネットワーク全体を管理します。 この仮説の正しさを検証するために、ノードを次数k（低、中、高）に応じて等しいサイズの3つのグループに分割しました。 写真として。 2つの正準ネットワークモデル（ Erdos - Renyi 35.36およびscaleless 15.37-39 ）の 2a、b では、ドライバーノードのシェアは、ハブ間よりも程度の低いノード間で大幅に高くなっています 。 図 2c、ドライバーノードの平均次数のプロットが表示されます。
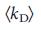、平均的な程度から、 
、表1の各ネットワークに対して、複数のネットワークモデルに対して。 すべての場合 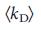類似よりも大幅に少ない 、実際のシステムとシミュレートされたシステムでは、ドライバーノードは通常ハブではないことを示します。
ネットワークの制御可能性を決定するトポロジ機能を決定するために、完全なランダム化手順（RAND-ER）を使用して各実ネットワークのランダム状態を選択しました。これにより、ネットワークはNおよびL定数のErdoS-Renyi指向のランダムネットワークになります。 複数のネットワークでは、間に相関関係はありません
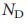ソースネットワークと 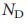そのランダム化された状態（図2d）、したがって、排除法による完全なランダム化では、 トポロジカル特性は制御可能性に影響を与えないと結論付けます。 また、入力度を保持する40.41度のランダム化（RAND度）を適用しました。 
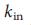、および出力度、 
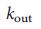、各ノードは変更されませんが、相互に接続されているノードをランダムに選択します。 観測された6桁の違いにもかかわらず、 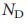この手順は変わりません 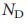実質的に。 したがって、 システムの制御性は、ネットワークノードの次数の分布に大きく依存します。 
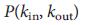、これは2番目に重要な結論です。 彼は言う 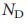基本的に各ノードの着信および発信リンクの数によって決定され、リンクが示す場所に依存しません。
管理性への分析的アプローチ
度の分布の重要性により、分析的に決定することができます
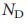任意のネットワーク 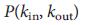。 addle 点法 42-44を使用して 、一連の自己矛盾のない方程式（セクションIV、 追加情報 ）を取得しました。その入力は度の分布であり、その解は平均に対するものです。 （または 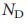）と互換性のあるすべてのネットワーク実装向け 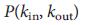、3番目の重要な結果です。 写真として。 分析的に計算された2 f 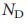と完全に一致 
（したがって、正確な値と十分に一致する必要があります 
）、さまざまなネットワークパラメータの影響を調査するための効果的な分析ツールを提供します 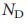。 addle点法は分析的な解決策を提供しませんが、依存性を得ることができます 熱力学的限界の主要なネットワークパラメーターから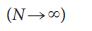 
。 たとえば、Erdos-Renyi指向のネットワークの場合、 概して 正しく 
（4）。 限界までスケールレスネットワークの場合、大規模な場合 38 、指数付き 
方程式があります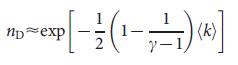 
（5）制限内 
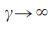同じ依存を持っています 、および方程式（4）。 式（5）から、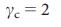 
無限のスケールレスネットワークの管理性の重要な指標であり、 
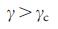有限数のノードを介してシステム全体を制御できます（つまり、 
） のために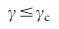 
、熱力学的限界では、絶対にすべてのノードを制御する必要があります（つまり、 = 1）。 に注意してください 
とは異なる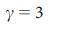 
、これは不一致によるウイルス拡散に対する耐性から31-33.45の多くのネットワーク現象の重要な指標です 
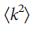。 ErdoS-Renyiやスケールレスネットワークなどのネットワークの分析計算を検証するために、数値依存性を決定しました から 漸近的な指数関数的依存性を確認します から 方程式（4）および（5）で予測されるとおり。 さらに、予測値 の数値結果とよく一致します 
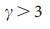（図3 d、e）。 しかし、近所で 
、 、サドルポイント法で予測されるように、正確な値から外れます のために重要である程度の相関関係のため 、およびスケールレスネットワーク39.46 （セクションIV.V 追加情報 ）の構築中にトリミングされた学位を導入することで排除できます。 式（5）はまた、 増加すると減少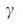 
（固定用 ）、それを示す 次数の不均一性に依存し、接続の少ないノードと接続の多いノードの違いを表します。 次の程度の不均一性を特定しました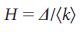 
どこで 
次数の分布から取得したノードのすべてのペア（iおよびj）の次数の平均絶対差 
。 すべてのノードが同じ次数を持つネットワークの場合、次数不均一性はゼロ（H = 0）です。たとえば、ノードの入力および出力次数が次のように減少するランダム正則有向グラフ（図3 a） / 2、ただしノードはランダムに接続されます。 のために > = 2、このグラフは常に完全に一致します 47 （グラフのすべての頂点を含む一致）。これは、1つのドライバーノードがシステム全体を制御できることを意味します（ 追加情報のセクションIV.B1）。
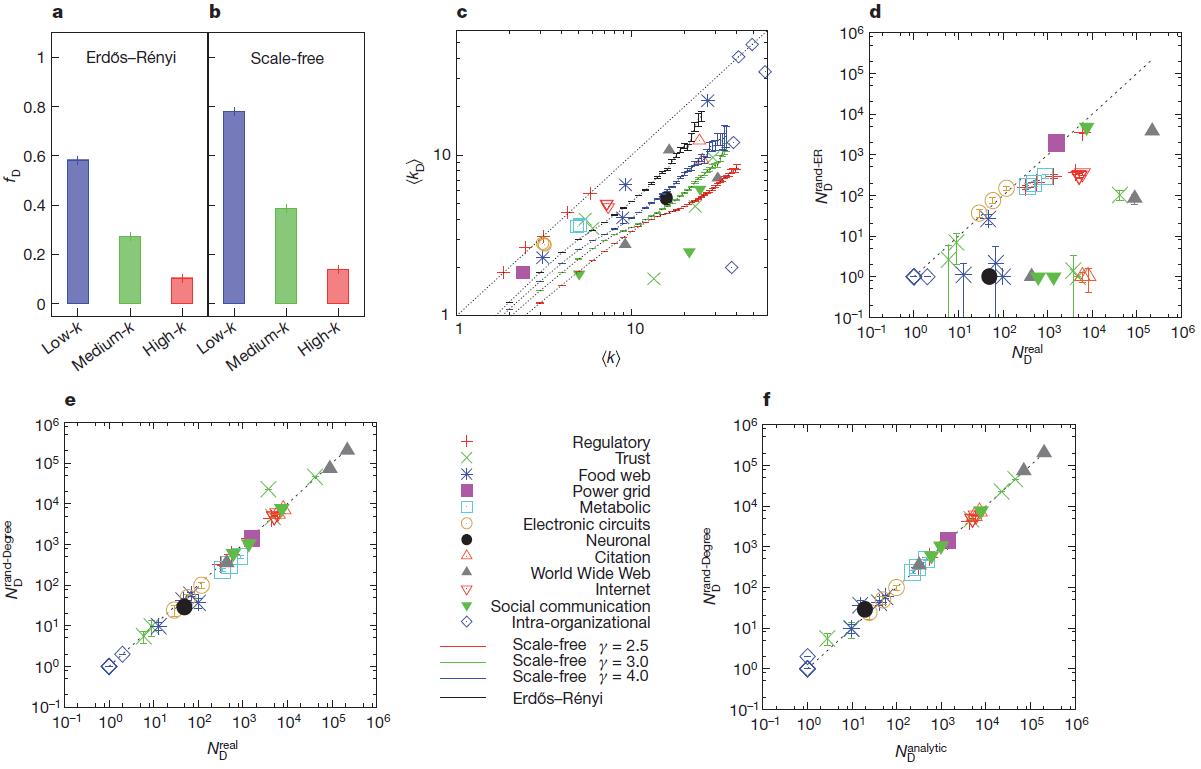
図2 | ドライバーノードの動作の特性と予測（
）
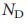a、b、ネットワークモデルでのハブの役割。 バーはドライバーノードの割合を示し、
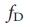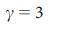、N = 10 4の 2つのネットワークモデル、Erdos-Re'nyi（a）およびスケールフリー（b）の低、中、および高度のノードを持つノード間 = 3（ ）、ドライバーノードは通常ハブではないことを示しています。 ErdoS-Re'nyiおよびスケールレスネットワークは静的モデル38から生成され、結果は100の実装で平均されます。 図に示すように、エラーバー（メイン列の上）は、値自体よりも小さくなっています。 c、実ネットワークおよびモデルネットワークのすべてのノードの平均度合いと比較したドライバーノードの平均度合いは、実際のシステムではハブがドライバーノードではないことを示しています。 d、ドライバーノードの数 
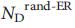表1にリストされているネットワークの完全にランダム化されたバージョンについて、正確な値と比較して得られた、 。 e、ドライバーノードの数 表1に示すネットワークのランダムバージョンの次数を保存して取得 。 f分析的に計算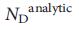 
addle点法を使用して取得したものと比較 。 dfでは、データポイントと不確実性（SEM）は、ランダム化されたネットワークの1000の実現から決定されました。
ランダムな規則的な有向グラフからErdoS-Renyiタイプのネットワーク（図3 b）に移動すると、不均一性の度合いが増加し、最終的には減少します
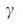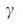スケールレスネットワークへ（図3 c）。 一般に、ドライバーノードの共有、 一定に保ちながら、Hとともに単調増加 （図3 f）または （図3 g）。
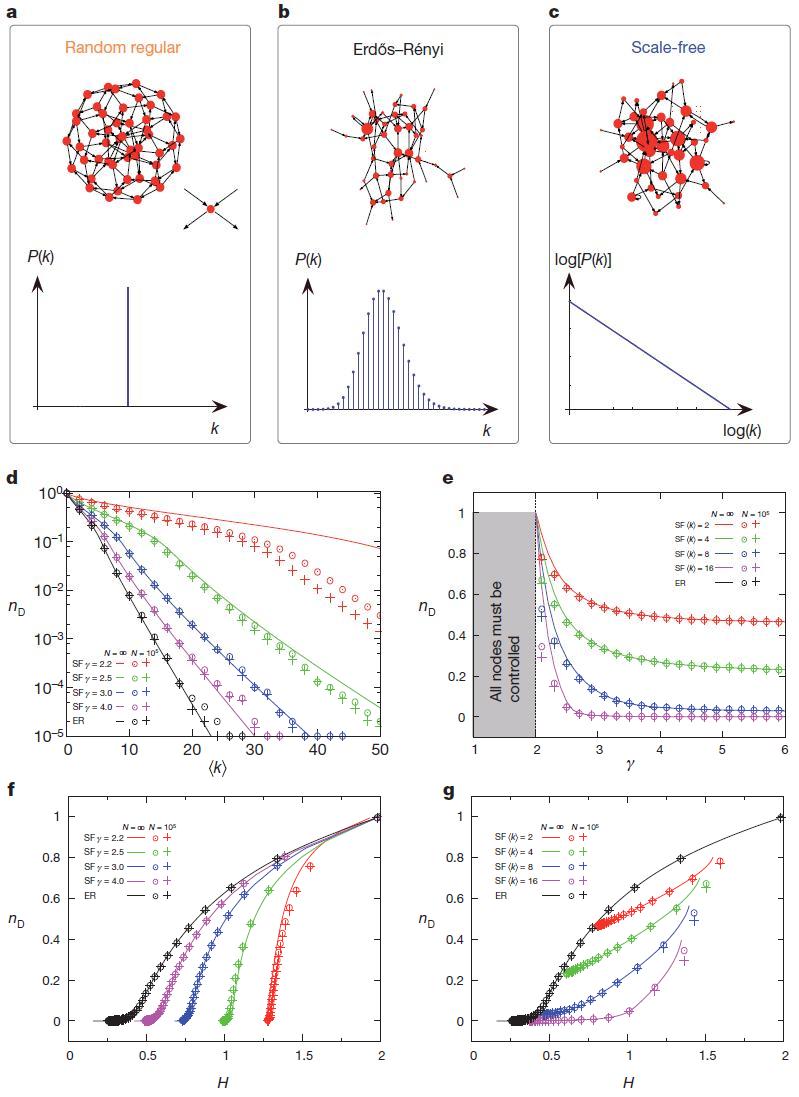
図3 | ドライバーノードの数に対するネットワーク構造の影響。 a – c、
調査したネットワークモデルの特性。 ここに示されている、ランダムに方向付けられたグラフ（ a ）
= 4は、次数分布が最も均一なネットワークです。 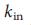= = 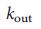/ 2すべてのノード。 Erdos – Renyiネットワーク（ b ）にはポアソン次数分布があり、それらの次数不均一性が決定されます 。 スケールフリーネットワーク（ c ）には度のべき法則分布があり、度の大きな不均一性につながります。 d 、ドライバーノードの密度、 の機能として Erdo – Renyi（ER）およびスケールレス（SF）ネットワークの異なる値 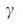。 スケールレスとエルドスの両方– Renyiネットワークは、N = 10 5の静的モデル38から生成されます。 線は分析結果であり、予想限界を使用する点法を使用して計算されます 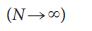度分布。
シンボルは、構築された離散ネットワークに対して計算されます。円は、最大一致法による正確な計算結果を示し、十字は、構築されたネットワークの正確な次数シーケンスを使用したaddle点法によって得られた分析結果を示します。 大規模
、 一番下のページN -1 、つまり唯一のドライバーノードに近づきます 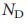=サイズがN. eのネットワークでは1 の機能として 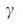固定のスケールレスネットワーク用 。 無限のスケールレスネットワーク向け -> 1以降 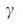-> = 2、つまり、ネットワーク全体を制御するには、ほぼすべてのノードを制御する必要があります。 有限のスケールレスネットワークの場合、 -> 1以降 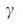-> 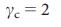つまり、ネットワーク全体を制御するためには、ほぼすべてのノードを制御する必要があります。 有限のスケールレスネットワークの場合 以来最大に達する 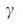近づいている （ 追加情報 ）。 f Erdosの次数不均一性Hの関数として– Renyiネットワークとスケールレス固定ネットワーク 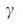そして変化する 。 g ErdosのHの関数としてのnD – Renyiネットワークと固定のスケールレスネットワーク そして変化する 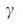。 増加とともに 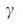、曲線は、対応する値でErdoS-Renyiネットワークの結果（黒）に収束します 。
これらの結果をまとめると、ネットワークの密度が高いほど、それを制御するために必要なドライバーノードが少なくなり、平均的な程度の小さな変化が変化を引き起こすことがわかります。
スケール順。 さらに、ノードの程度の差が大きいほど、システムを制御するために必要なドライバーノードの数が多くなります。一般に、放電された異種のネットワーク、つまりこれらの特性は、セルラーネットワークやインターネットなどの複雑なシステムでよく見られます。13-16は、そのようなシステムの制御が難しいことを強調して、より多くのドライバーノードを必要とします。
制御の安定性
は避けられない、ネットワーク内のいくつかのリンクを、欠けている、我々は3つのカテゴリのいずれかに各コンタクトを分類状況でネットワークを管理する方法の信頼性は、我々の能力を参照する（図1、D、G、J）：
«クリティカル»消失した場合、完全な管理性を維持するためにドライバーノードの数を増やす必要があります。
ドライバーノードの現在のセットに影響を与えずに削除できる場合は「余分な」、または
重大でも不要でもない場合は「普通」。図4は、各実ネットワークのクリティカル
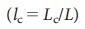、冗長、
および通常の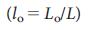
リンクの密度を示しています。また、ほとんどのネットワークにはクリティカルリンクがほとんどないかまったくありません。ほとんどの接続は一般的です。つまり、一部の管理構成で役割を果たしますが、これらのネットワークは不在でも管理できます。図4 |持続可能性管理のコンテキストでカテゴリをリンクします。
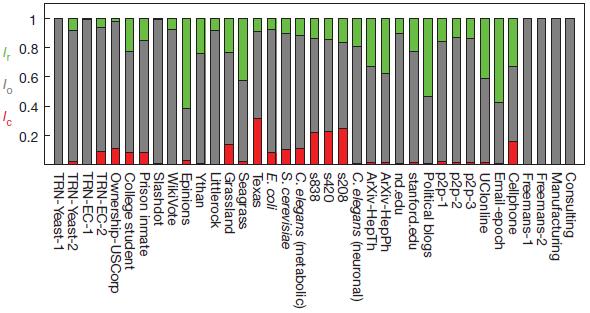
表1に示す実際のネットワークのクリティカル（赤、LC）、冗長（緑、LR）、および通常（灰色、LO）のリンクのシェア。リンク損失に対する管理を強化するには、クリティカルリンクのみを正式に2倍にするだけで十分です。これらのリンクは冗長であるため、システムに重要なリンクがないことを確認してください。
決定する要因を認識するために
、 
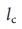そして 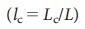図 5 A、C、F、モデルシステムに対する依存性を示します。動作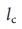は簡単に理解できます：小規模の場合、すべての接続は管理にとって重要です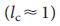
。以下のように増加すると、ネットワークの冗長性が減少すると共に増加します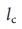 。冗長性の増加は、過剰結合の密度、、常に増加する必要があることを示唆していますが、そうではありません：臨界値で最大に達します 、 
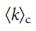、その後彼は倒れます。この非単調な挙動は、2つのトポロジー的に異なるネットワークセグメント、コアとリーフ43間の競合の結果です。コアは、「葉の多い」葉の除去48を適用した後、ネットワークに残っているノードのコンパクトなクラスターであり、葉は、葉の除去の前または間に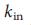= 1または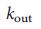= 1のノードです。コアは、移行部の浸透を介して終了します（図5、B、D）：K < 、 
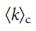そのため、システムは葉だけで構成されます（図5 E）。 で = 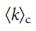、小さなコアが表示され、葉の数が減ります。ErdoS-Renyiネットワークの場合、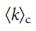= 2e = 5.436564 と仮定します。これは、数値結果（図5 a、b）と一致し、一致する値
と
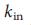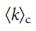どこで 最大に達する。確かに、それは時に沈静化し始めたためので、 > 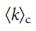異なる最大一致の数は指数関数的に増加し（追加情報のセクションIV.C ）、その結果、リンクが制御構成に関与しない可能性が減少します。スケールレスネットワークの場合、同じ動作を観察しますが、警告は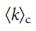減少します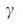（図5、c、d）。
議論と結論
管理は最も複雑なシステムの中心的な問題の1つですが、定量的な方法を使用してこれらの問題を研究する一般的な理論がないため、加重指向のネットワーク（ほとんどの場合、構成実際のシステムにあります）。実際、大規模ネットワークに対するカルマン制御可能性ランク条件（式（3））の適用は計算上過剰であり、ノード数が数十以下のネットワークへの以前の研究の適用を制限しています17-19。ここでは、任意のトポロジとサイズでネットワーク管理の問題を解決するためのツールを開発しました。私たちの主な結論は
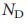これは主に、私たちは、分析的依存性を予測するために統計物理学のツールを使用することができ、分布の程度によって決定される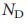の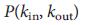取り扱い上のネットワーク効果のトポロジーを研究するための一般的な形式主義を提供します。図5 | 持続可能性管理。a、 Erdos – Renyiネットワーク上のクリティカル（赤、LC）、冗長（緑、LR）、および通常（灰色、LO）結合の割合の依存性：lrは
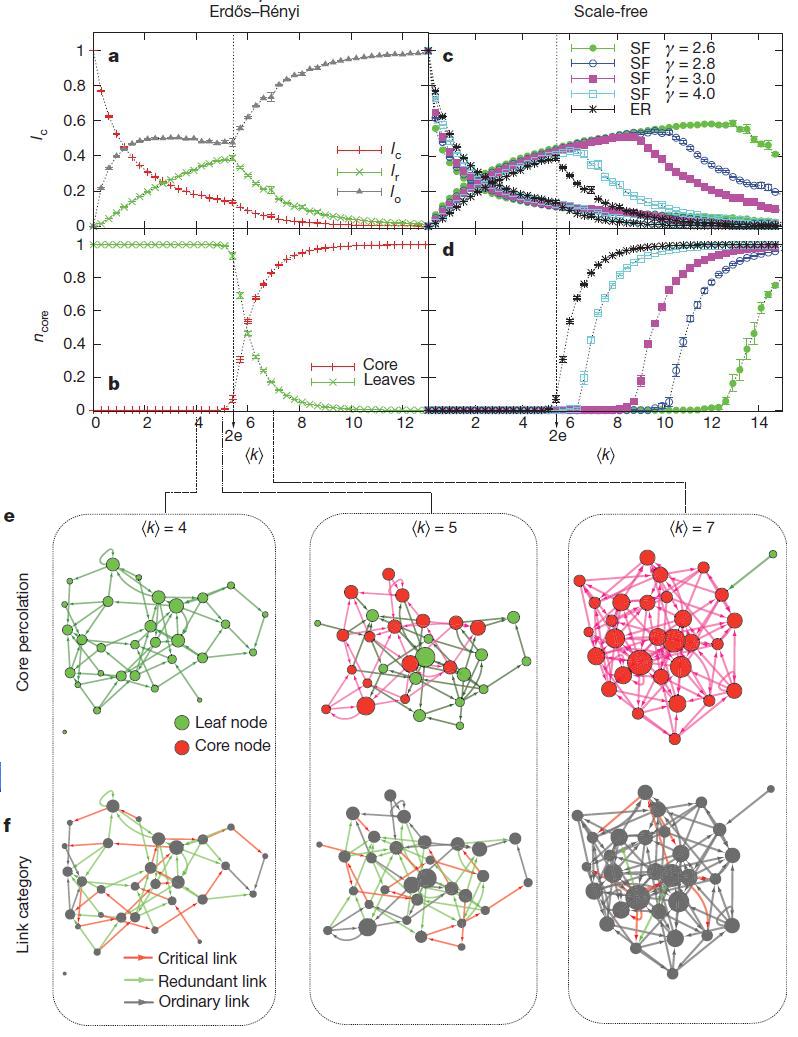
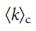= = 2e、および微分LC = 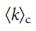。 b、 Erdosのコアリーク– Renyiネットワークが発生するのは = = 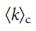2e、これはLRのピークを説明します。c、d、 aおよびbと同じですが、スケールレスネットワーク用です。Erdos – Renyiネットワークとスケールレスネットワーク38はN = 10 4であり、結果はsemとして定義されたエラー値で10回の実現に対して平均されます。点線は慣例によってのみ示されています。e、小さなエルドスのコア（赤）と葉（緑）–異なる値を持つRenyiネットワーク（N = 30） （ = 4、5、7）。ノードのサイズは、ノードの次数に比例します。f、 Erdos上のクリティカル（赤）、冗長（緑）、および通常（灰色）通信–対応する値を持つRenyiネットワーク 。
ここで紹介するアプローチでは、多くの質問が提起され、その答えにより、困難な状況での管理のタスクに対する理解がさらに深まる可能性があります。たとえば、私たちの分析作業が無相関のネットワークに焦点を当てているという事実にもかかわらず、我々が開発してきたことを、アルゴリズムの方法が決定することができます
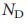の相関関係の役割の問題のための体系的な基礎を提供、任意のネットワークのために40、49、50。総合すると、ネットワークサイエンスと制御理論のツールを組み合わせることにより、制御性の多くの側面を任意のネットワークの分析方法で正確に研究でき、複雑なシステムの理解を深めるための新しい方法を開くことができます。
記事「複雑なネットワークの管理性」への追加情報Nature誌のウェブサイト上で利用できる
翻訳の著者によって提供さdopolnitelyunuyu情報へのリンク
1. 遺伝子制御ネットワークにおける転写因子の濃度を
2 理論のマッチング
3. 基準カルマン制御ランク
4 力ずくで検索
5. 方法鞍点
翻訳を用意Rabchevskyユージーン。
1.カルマン、RE線形力学系の数学的記述。 J. Soc。インダス適用数学。 Ser。 A 1、152–192（1963）。
2. Luenberger、DGダイナミックシステム入門：理論、モデル、およびアプリケーション（Wiley、1979）。
3. Slotine、J.-J。 ＆Li、W. Applied Nonlinear Control（Prentice-Hall、1991）。
4. Kelly、FP、Maulloo、AK＆Tan、DKH通信ネットワークのレート制御：シャドー価格、比例公平性、安定性。 J.オペラ。解像度Soc。 49、237–252（1998）。
5. Srikant、R。The Mathematics of Internet Congestion Control（Birkha¨user、2004）。
6.チェン、M。、ロー、SH、カルダーバンク、AR＆ドイル、JC最適化分解としての階層化：ネットワークアーキテクチャの数学的理論。手続きIEEE 95、255-312（2007）。
7. Wang、XFおよびChen、G。スケールフリー動的ネットワークのピンニング制御。 Physica A 310、521-531（2002）。
8. Wang、W.＆Slotine、J.-JE結合非線形振動子の部分収縮解析について。バイオサイバーン。 92、38-53（2005）。
9. Sorrentino、F.、di Bernardo、M.、Garofalo、F.＆Chen、G.固定による複雑なネットワークの制御可能性。物理学牧師E 75、046 103（2007）。
10. Yu、W.、Chen、G.＆Lu¨、J.複雑な動的ネットワークの同期の固定について。 Automatica 45、429-435（2009）。
11. Marucci、L. et al。遺伝子回路を調整可能な合成発振器または双安定スイッチに変える方法。 PLOS ONE 4、e8083（2009）。
12. Strogatz、SH複雑なネットワークの探索。 Nature 410、268–276（2001）。
13. Dorogovtsev、SN＆Mendes、JFF Evolution of Networks：Biological Nets to Internet and WWW（Oxford Univ。Press、2003）。
14.ニューマン、M。、バラバシ、A.-L。 ＆Watts、DJ The Structure and Dynamics of Networks（プリンストン大学出版局、2006）。
15. Caldarelli、G。スケールフリーネットワーク：自然とテクノロジーの複雑なWeb（Oxford Univ。Press、2007年）。
16. Albert、R.＆Baraba´si、A.-L.複雑なネットワークの統計力学。牧師Mod。物理学74、47–97（2002）。
17. Tanner、ProcのHG。第43回IEEE会議決定コントロール巻3、2467-2472（2004）。
18. Lombardi、A.＆Hoernquist、M.ネットワークの可制御性分析。物理学牧師E 75、56110（2007）。
19. Liu、B.、Chu、T.、Wang、L。、およびXie、G。リーダーの制御可能性–スイッチングトポロジを備えたフォロワー動的ネットワーク。 IEEE Trans。オートマトン。制御53、1009-1013（2008）。
20. Rahmani、A.、Ji、M.、Mesbahi、M。、およびEgerstedt、M。グラフ理論的観点からのマルチエージェントシステムの制御可能性。 SIAM J. Contr。最適48、162–186（2009）。
21. Kim、D.-H。＆Motter、AEスレーブノードと代謝ネットワークの制御可能性。 NJ Phys。 11、113047（2009）。
22. Mesbahi、M.＆Egerstedt、M. Multiagent Networksのグラフ理論的手法（プリンストン大学出版局、2010年）。
23. Motter、AE、Gulbahce、N.、Almaas、E.＆Baraba´si、A.-L.代謝ネットワークにおける合成レスキューの予測。 Mol。システム。バイオ4、168（2008）。
24.パストル・サトラス、R。＆ヴェスピニャーニ、A。インターネットの進化と構造：統計物理学アプローチ（Cambridge Univ。Press、2004）。
25. Lezon、TR、Banavar、JR、Cieplak、M.、Maritan、A。、およびFedoroff、NVエントロピー最大化の原理を使用して、遺伝子発現パターンから遺伝的相互作用ネットワークを推測します。手続きNatl Acad。科学USA 103、19033-19038（2006）。
26.リン、C.-T。構造制御性。 IEEE Trans。オートマトン。コントラクト19、201–208（1974）。
27.シールド、RW＆ピアソン、JBマルチ入力線形システムの構造制御性。 IEEE Trans。オートマトン。コント21、203–212（1976）。
28. Lohmiller、W.＆Slotine、J.-JE非線形システムの収縮解析について。 Automatica 34、683–696（1998）。
29. Yu、W.、Chen、G.、Cao、M.、Kurths、J。有向トポロジーと非線形ダイナミクスを備えたマルチエージェントシステムの2次コンセンサス。 IEEE Trans。システム。男サイバーン。 B 40、881–891（2010）。
30.二部グラフの最大マッチングのためのHopcroft、JE＆Karp、RM Ann5 / 2アルゴリズム。 SIAM J. Comput。 2、225–231（1973）。
31. Albert、R.、Jeong、H.＆Baraba´si、A.-L.複雑な
ネットワークのエラーおよび攻撃に対する耐性。 Nature 406、378–382（2000）。
32. Cohen、R.、Erez、K.、Ben-Avraham、D。＆Havlin、S。ランダムな故障に対するインターネットの回復力。物理学牧師レット。 85、4626–4628（2000）。
33.牧師-Satorras、R。＆Vespignani、A。スケールフリーネットワークでの流行の広がり。物理学牧師レット。 86、3200-3203（2001）。
34.西川、T。、モッター、AE、ライ、Y.-C。 ＆Hoppensteadt、FC発振器ネットワークの不均一性：小さい世界は同期しやすいですか？物理学牧師レット。 91、014101（2003）。
35.Erdo˝s、P.＆Re´nyi、A.ランダムグラフの進化について。公開数学。研究所ハングAcad。科学5、17-60（1960）。
36. Bolloba´s、B。Random Graphs（Cambridge Univ。Press、2001）。
37.バラバシ、A.-L。＆アルバート、R。ランダムネットワークでのスケーリングの出現。 Science 286、509-512（1999）。
38. Goh、K.-I.、Kahng、B.＆Kim、D.スケールフリーネットワークにおける負荷分散の普遍的な動作。物理学牧師レット。 87、278701（2001）。
39. Chung、F.＆Lu、L.与えられた次数シーケンスを持つランダムグラフの接続コンポーネント。アン。結合します。 6、125-145（2002）。
40. Maslov、S.＆Sneppen、K.タンパク質ネットワークのトポロジーにおける特異性と安定性。 Science 296、910–913（2002）。
41. Milo、R. et al。ネットワークモチーフ：複雑なネットワークの単純な構成要素。 Science 298、824–827（2002）。
42. Me´zard、M.＆Parisi、G. Bethe格子スピングラスの再検討。ユーロ物理学J. B 20、217-233（2001）。
43. Zdeborova´、L.＆Me´zard、M.ランダムグラフの一致数。 J.スタットメカ05、05003（2006）。
44. Zhou、H.＆Ou-Yang、Z.-c.ランダムグラフの最大一致。 Prehttp：//arxiv.org/abs/cond-mat/0309348æ（2003）でプレプリント。
45. Callaway、DS、Newman、MEJ、Strogatz、SH＆Watts、DJネットワークの堅牢性と脆弱性：ランダムグラフでの浸透。物理学牧師レット。 85、5468-5471（2000）。
46. Bogun〜a´、M.、Pastor-Satorras、R。＆Vespignani、A。スケールフリーネットワークでのカットオフと有限サイズ効果。ユーロ 物理学 J. B 38、205–209（2004）。
47. Lova´sz、L.＆Plummer、MDマッチング理論（American Mathematical Society、2009年）。
48. Bauer、M.＆Golinelli、O.ランダムグラフのコアパーコレーション：臨界現象分析。ユーロ 物理学 J. B 24、339-352（2001）。
49.ニューマン、MEJAssortativemixinginnetworks.Phys.Rev.Lett。89,208701（2002）。
50.パストル・サトラス、R。、ヴァスケス、A。＆ヴェスピニャーニ、A。インターネットの動的および相関特性。物理学 牧師 レット。87、258701（2001）。