情報転送の開発の歴史における最も重要な飛躍は、デジタルデータ転送システムの使用でした。 アナログ信号を使用するには、システムで送信される情報の大きな冗長性が必要であり、ノイズの蓄積などの重大な欠点もあります。 アナログ信号をデジタルに変換し、保存し、送信し、アナログ形式に戻すためのさまざまな形式のコーディングは、20世紀後半に急速な発展を始め、21世紀の初めには、アナログシステムがほぼ置き換えられました。
通信システムを構築するときに解決する必要がある主な問題は、1948年にクロードシャノンによって最初に策定されました。
通信システムの主な特性は、空間と時間の特定のポイントで、別のポイントで選択されたメッセージを正確またはほぼ再現する必要があることです。 通常、このメッセージは意味をなしますが、割り当てられたエンジニアリングの問題を解決するために絶対に重要ではありません。 最も重要なことは、送信されるメッセージは、考えられるメッセージのファミリーから選択されることです。
コミュニケーションの問題に関するこのような正確で明確な声明は、コミュニケーションの発展に多大な影響を与えました。 情報理論として知られるようになった新しい科学分野が登場しました。 シャノンによって正当化された主なアイデアは、信頼できる通信はデジタルでなければならないということです。 通信の問題は、2進数（ビット）の送信と見なされる必要があります。 これで、送信された情報と受信された情報を明確に比較できます。
物理信号伝送チャネルは完全に信頼できるものではないことに注意してください。 たとえば、チャネルを損ない、送信されたデジタル情報にエラーを導入するノイズ。 シャノンは、特定のかなり一般的な条件下では、原則として、信頼性の低いチャネルを使用して、任意の高い信頼性で情報を送信することが可能であることを示しました。 したがって、たとえば信号のパワーを上げるなど、ノイズのチャネルをクリアする必要はありません（これは高価であり、多くの場合不可能です）。 代わりに、デジタル信号の効率的なコーディングおよびデコーディングスキームを開発する必要があります。
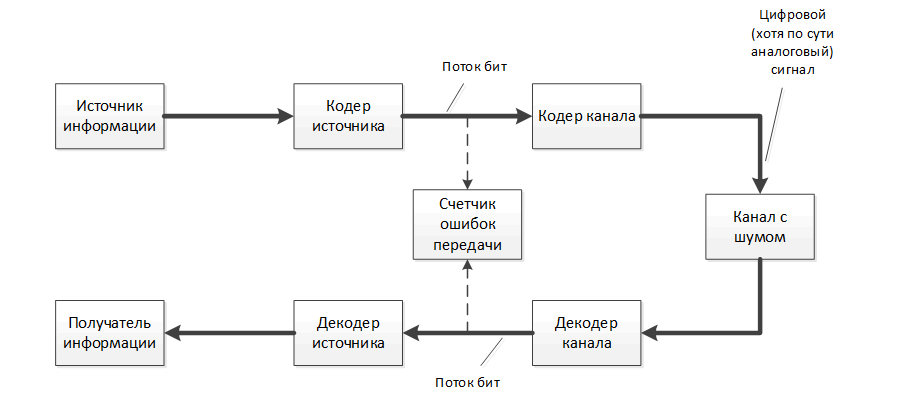
チャネルコーディング（信号コード構成の選択）のタスクは、チャネルの既知の特性に基づいて、入力シンボルをチャネルに送信するエンコーダーを構築し、受信機によって最大限の信頼性でデコードされます。 これは、送信されたデジタル情報に追加のチェック文字を追加することで実現されます。 実際には、電話ケーブル、衛星放送受信アンテナ、光ディスク、コンピューターのメモリなどがチャンネルとして機能します。 ソースコーディングのタスクは、ソース信号のコンパクトな（短縮された）記述を生成するソースエンコーダーを作成することです。 信号のソースは、テキストファイル、デジタル画像、デジタル化された音楽、またはテレビ放送です。 このソース信号の短い説明は不正確な場合があります。その場合、受信およびデコード後に復元された信号とその元の信号との不一致について話す必要があります。 これは通常、アナログ信号をデジタル形式に変換（量子化）するときに発生します。
直接定理：
メッセージレートが通信チャネルの帯域幅よりも小さい場合、ブロック長が無限大になるとデコードエラーの平均および最大確率がゼロになる傾向があるコードとデコード方法があります。
言い換えると、干渉のあるチャネルの場合、ソースのパフォーマンスのみがチャネル容量を超えない場合、任意の高度の忠実度でメッセージが送信されるコーディングシステムを常に見つけることができます。
逆定理：
伝送速度が帯域幅よりも大きい場合、つまり、伝送されるブロックの長さが長くなるにつれてエラーの確率がゼロになる傾向のある伝送方法はありません。Wiki
加法性ホワイトガウスノイズの場合、シャノンは次の式を取得しました。
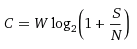どこで
C-チャネル帯域幅、ビット/秒;
Wはチャネル帯域幅、Hzです。
Sは信号電力、Wです。
Nはノイズパワー、W
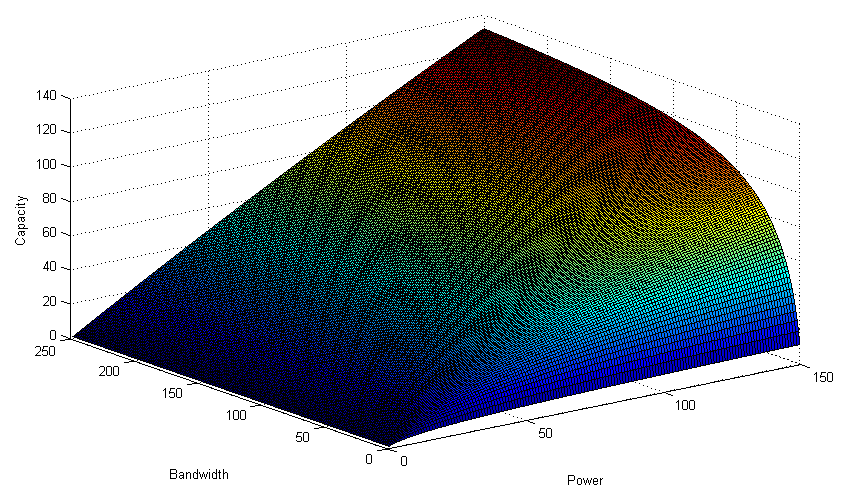
（わかりやすくするためのグラフ、N 0 = constでのC（W、P）の依存性、天井からの値、それらを見ないでください）
なぜなら ABGSの電力はチャネル帯域幅に比例して増加します。チャネル容量には限界C max =（S / N 0 ）log（2）があり、無限に広い周波数帯域（電力で線形に増加）があります。
どこで
ηはスペクトル利用効率、ビット/ s / Hzです。
T R-情報転送速度、ビット/秒。
Wはチャネル帯域幅、Hzです。
それから
ビットエネルギー値を使用する（複雑な信号コード構造を持つ信号の場合、ビットあたりの平均エネルギー値がわかります）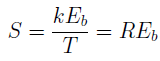 
どこで
kは、チャネルに送信される文字ごとのビット数です。
T-文字の長さ、s;
Rはチャネルの伝送速度、ビット/ sです。
E b-チャネル内の1ビットの送信のエネルギー。
N 0-ノイズパワーのスペクトル密度、W / Hz。
私たちは得る
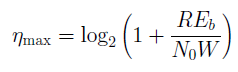または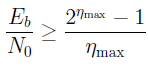 
。
シャノンの制限は次のとおりです。
この制限は、コーデックのないチャネル（R = T R ）にとって意味があります。このような効率を実現するには、受信ワードの長さが無限でなければなりません。 エラー訂正コーディングコーデックを使用するチャネルの場合、E bはチャネルビットではなく1つの情報を送信するエネルギーとして理解される必要があります（異なる解釈があり、別のバージョンを聞く準備ができています）=>チャネルのE b / N 0は速度によってこの値と異なりますコード（1 / 2、3 / 4、7 / 8 ...）
したがって、チャネル内の信号対雑音比（E b / N 0 ）には制限があり、任意の小さなエラー確率をより高いノイズレベルで達成できるデータ伝送システムを構築することは不可能であることがわかります（わずかなシステムが存在する可能性があります）エラーの確率、最大限の敬意を払って！）
文学
ギャラガーR. 「情報理論と信頼できるコミュニケーション」-M .:「ソビエトラジオ」、1974年。
Salomon D. 「データ、画像、音声の圧縮」-M。：「Technosphere」、2004
関心をお持ちの方は、続きとして、イラストを掲載した記事を書いたり、シャノンの境界に関するシグナルコードの構成の有効性を比較したりして、ご清聴ありがとうございました。