Linux用の1k / 4kイントロの作成、パート4

すべての最高の、私の過度に忍耐強い友人！

覚えている人はほとんどいませんが、 2番目の部分では、画面全体に長方形があり、そこに数百バイトのバイトがあり、1年半の間、コードと心の空白を創造性で埋めるという問題に直面しています。



結局のところ、たった2つの三角形で描画できるものは何でしょうか？ スクエア？ フラクタル？ 市内中心部でメガトンの電力爆発を飛ぶ？ 現実が終わり現実が始まる狂気に制限はありますか？ 光線を適切にケアする方法、それらを養う方法、および何を反映するかについては、デモメイキングに関する一連の記事の突然の続きで学びます！

はじめに

プロトタイピングの利便性のために、 shadertoy.comを使用することをお勧めします。例へのリンクがそこにあります。 したがって、代替オペレーティングシステムのユーザーでさえ、ここにあるこのすばらしいすべてに没頭できます。

はい、暗黙的に使用するWindows WebLでは、何らかの理由で、誰もがANGLEを通じて実装することを好みます。ANGLEは、常習者であり、複雑なシェーダーをロックすることで有名です。 したがって、ネイティブのOpenGLを有効にすることをお勧めします（chrome：-- use-gl = startup at startup）

そして、はい、少なくともGTX 4xxまたはHD 6xxxのような非常に強力な最新のビデオカードが必要です（そして、Intelは決して笑いません）。そうでなければ、フィルムストリップがあります。

はじめに-2

シェーダーとは何か、その由来と理由については詳しく説明しません-これは別の一連の記事のトピックであり、存在しません、笑-構文に応じて変数gl_FragColor



現在のピクセルの色をgl_FragColor



必要があることを理解するのに十分ですその座標はgl_FragCoord



（ピクセル単位）とiGlobalTime



時間です（これは、GLSL標準ではシェーダーの特異性です。もちろん、時間については何もありません）。

GLSLには、ベクトル型とマトリックス型のvecN



、 matN



、およびあらゆる種類の数学関数とそうではない関数の標準ライブラリがあります。 好奇心for 盛な人のためのHref（シェーダーがOpenGL ES 2.0から継承されたWebGLであるため、GL ES）。

リアルタイムレイトレーシング

10〜15年前には達成不可能な夢と考えられていたこと、つまりリアルタイムでの光線追跡を行うことを提案します。 現代のビデオカードは非常に生産的であるため、そうです。

主なアイデアは、画面上のピクセルの色を決定し、そこから光線を開始し、どのオブジェクトに対して静止するかを探すことです。その後、オブジェクトと交差点の知識を使用して、何らかの方法で照明を計算し、目的の色を形成します。

光線が特定のオブジェクトを交差するかどうか、また交差する場合はどの時点で判断できますか？ たとえば、光線と目的のオブジェクトの交点の方程式を書き、それらを解析的に解決することができます。 この方法は、球や平面よりも複雑なものの場合、非常にすぐに面倒になることが簡単にわかります。 これは良くありません。火星に猫のパックの着陸を描きたいので、別の方法、つまり距離関数の球面トレースを使用します。

私からあなたへ

距離関数は、空間内の各点の最も近いジオメトリまでの距離を返すR3-> R関数です。 実際には、単純な図であっても、このような関数を書くことは、分析的交差よりも簡単です。 例：

• ボール： length(at) - R
  
  
  
  
• 平面： dot(at,N) - D
  
  
  
  
• length(max(abs(at)-size), 0.))
  
  
  
  ： length(max(abs(at)-size), 0.))
  
  
  
  
• シリンダー（Y）： length(at.xz) - R
  
  
  
  

さらに、このような関数を使用すると、建設的なジオメトリを簡単に作成できます。

• 結合： min(f, g)
  
  
  
  
• 交差点： max(f, g)
  
  
  
  *
• 減算： max(f, -g)
  
  
  
  *

そして、変換-入力サンプリングベクトルを以下で変換するだけで十分です。

• キャリー： at-vec3(pos)
  
  
  
  
• 回転など： at*mat3(< >)
  
  
  
  （スケーリングの場合、返された距離を縮小する必要があることに注意してください）

*-厳密なFと距離ではなく、推定

球状トレース

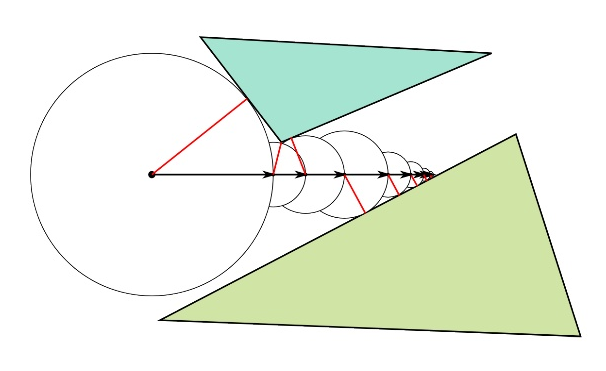
そのような機能を持つビームの交差点を見つける方法は？ シンプルでエレガントなソリューションの1つは、球状のトレースです。 アルゴリズムは次のとおりです。

1. 点Oから方向Dにビームを開始します。
2. 点Oで関数の値に等しいdを取得します
3. 点Oを距離dだけ方向Dに移動します
4. dが選択されたしきい値よりも大きい場合、ステップ2に戻ります。
5. 現在の点Oは、指定された精度の望ましい交差点であり、終了します

GLSLでは、単純なトレース関数は次のようになります。

 float trace(vec3 O, vec3 D) { float L = 0.; for (int i = 0; i < MAX_STEPS; ++i) { float d = world(O + D*L); L += d; if (d < EPSILON) break; } return L; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合計、原点が半径1の球体の単純なマーチャーは、たとえば次のようになります（移動距離の視覚化）。

 // ,      #define MAX_STEPS 32 #define EPSILON .001 //         float world(vec3 a) { return length(a) - 1.; //   1   } //      O    D.    float trace(vec3 O, vec3 D) { float L = 0.; //   for (int i = 0; i < MAX_STEPS; ++i) { //  MAX_STEPS  float d = world(O + D*L); //      L += d; //     if (d < EPSILON*L) break; //     ,  } return L; //    } void main(void) { //     [-1., 1.] vec2 uv = gl_FragCoord.xy / iResolution.xy * 2. - 1.; //     uv.x *= iResolution.x / iResolution.y; //   vec3 O = vec3(0., 0., 3.); //      z ; -2.       -  vec3 D = normalize(vec3(uv, -2.)); //    float path = trace(O, D); //  ,    gl_FragColor = vec4(path * .2); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私たちの球体は疑わしく空中に垂れ下がっているので、例えば飛行機に置いてみましょう。

 float world(vec3 a) { return min(length(a) - 1., ay + 1.); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さあ、グレアやフリルのないシンプルな拡散スタートのために、照明をかきましょう。

単純なランベルトモデルでは、表面に入射する光はすべての方向に均一に散乱されると想定されているため、点の照度は法線と光源の方向の間の角度の余弦に比例します。 さらに、照明は光源からの距離の2乗として減少します。 さて、ソースの色と表面自体を忘れてはいけません。

コードでは、次のようになります。

 vec3 enlight(vec3 at, vec3 normal, vec3 diffuse, vec3 l_color, vec3 l_pos) { //        vec3 l_dir = l_pos - at; //  =      //  =   (=   ) //        (=   ) //       ,         return diffuse * l_color * max(0.,dot(normal,normalize(l_dir))) / dot(l_dir, l_dir); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

法線を取得するのは簡単です-距離関数の勾配です：

 vec3 wnormal(vec3 a) { vec2 e = vec2(.001, 0.); float w = world(a); return normalize(vec3( world(a+e.xyy) - w, world(a+e.yxy) - w, world(a+e.yyx) - w)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果：





何かが足りないですね。 球はまだぶら下がっていて、どういうわけか暗いようです。

目が完全にリアルで快適になるためには、影とガラスの影という2つの要素を追加する必要があります。



最初に、 vec3(.1)



または.2のようなものを好みの色に追加するだけで、ambeint照明を追加します。

カップシャドウはアンビエントオクルージョンでもあり、光源からだけでなく、あらゆる側面から飛んでくる光子によって表面が部分的に隠されている場合、現実世界からの効果の近似値です。

リアルタイムのトライドチャートでは、さまざまな程度の粘り強さの同様の効果を得るための多くの方法があります。 使用される手法では、標準的なアプローチは、ジオメトリの近接に関するシーン空間データの活用です。法線に沿っていくつかの手順を実行し、私たちをあいまいにする可能性のあるものがどれだけ近いかを判断します。 これはかなりウォッシュされていないハック（一般的に、この惑星で行うすべてのようなもの）ですが、かなり問題ないように見えます。

コードは次のとおりです。

 //    float occlusion(vec3 at, vec3 normal) { //  ,     float b = 0.; //    for (int i = 1; i <= 4; ++i) { //   .06 --     float L = .06 * float(i); float d = world(at + normal * L); //           b += max(0., L - d); } //   1    return min(b, 1.); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

通常の影はさらに簡単になります-ある点からのビームを光源に入れて、途中で何かに当たるかどうかを確認します。

 if (trace(at, normalize(l_dir), EPSILON*2.) < length(l_dir)) return vec3(0.);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

正確にその時点から開始することはできません。少し後退する必要があることに注意してください（宿題：なぜ？）



そして最後に、アンビエント照明の背景がマージされないように、黒化フォグをそこに配置します。

 color = mix(color, vec3(0.), smoothstep(0.,20.,path));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合計：

材料値

しかし、それはまだ灰色で単調です。 ボールと飛行機を異なる色にしましょう。 そして、ボールがメタリックなハイライトを持つようにします。

このためにmaterial_t



構造体を作成しましょう。

 struct material_t { vec3 diffuse; float specular; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

世界を個々の材料のジオメトリを返す関数に分割し、次の関数を記述します。

 //      material_t wmaterial(vec3 a) { //     material_t m = material_t(vec3(.5, .56, 1.), 200.); float closest = s_ball(a); //     --  float sample = s_floor(a); //     if (sample < closest) { //    closest = sample; //    --    m.diffuse = vec3(1.-mod(floor(ax)+floor(az), 2.)); m.specular = 0.; } return m; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、ライティング関数で色定数ではなくマテリアルを使用するだけで十分です。

最後のタッチにハイライトを追加します。 一般に、鏡面反射グレアは松葉杖でもあり、金属からの光の反射の実際の効果をシミュレートする試みです（これを行うことは物理的に正直に困難です-あらゆる種類のBRDF、レンダリング式、メトロポリスによるビームの揺れ、私が理解できない他の重い学術グラフィックスから始まります） ）、したがって、この効果を近似するためのさまざまな方法のスタックがあります。 ここでは、正規化されたBlinn-Fongメソッドを使用します。これは、法線と観測者と光源の間のハーフベクトルとの間の角度のコサインになります。 鏡面グレアは、マテリアルの拡散色から物理的に独立しています。

長い、短い、ここにコードがあります：

 if (m.specular > 0.) { // , ,  --        vec3 h = normalize(normalize(l_dir) + normalize(eye-at)); //      color += l_color * pow(max(0.,dot(normal,h)), m.specular) * (m.specular + 8.) / 25.; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合計：

エンドウ豆の壁はどうですか

私たちのボールは疑わしいことに何も反映していないので、禁止しましょう。

反射フィールドを材料に追加し、観察者で反射される入射光の割合を指定します。

トレースをリフレクションループでラップしましょう。

 //        vec3 result_color = vec3(0.); //    float k_reflectivity = 1.; for (int i = 0; i < MAX_REFLECTIONS; ++i) { //    float path = trace(O, D, 0.); //      ,  if (path < 0.) break; // ,    vec3 pos = O + D * path; vec3 nor = wnormal(pos); //     material_t mat = wmaterial(pos); //   vec3 color = .15 * (1. - occlusion(pos, nor)) * mat.diffuse; //    color += enlight(pos, nor, O, mat, vec3(1., 1.5, 2.), vec3(2.*cos(t), 2., 2.*sin(t))); color += enlight(pos, nor, O, mat, vec3(2., 1.5, 1.), vec3(2.*sin(t*.6), 3., 2.*cos(t*.6))); // -  color = mix(color, vec3(0.), smoothstep(0.,20.,path)); //      result_color += k_reflectivity * color; //     k_reflectivity *= mat.reflectivity; // ,      if (k_reflectivity < .1) break; //        D = normalize(reflect(D, nor)); O = pos + D * EPSILON*2.; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

シーンにあらゆる種類の追加を追加します。フクロウを描く方法は次のとおりです。





しかし、これはすべて悪いです。

悪い、悪い、悪い。

これらはすべて距離関数なしで描画でき、さらに高速に動作します。 したがって、すべてを捨てて、最初からジオメトリの描画を開始しましょう。



しかし最初に、無秩序の世界への小さな余談。

カオス理論

完全に滑らかな球体と平面はすべて良好ですが、合成的すぎます。 現実の世界は不規則で不完全であり、一般的にはくそでできています。 したがって、あなたの写真でそれに近づくために、あなたはあなたの好みにそれの混pinのピンチを加える必要があります。

ノイズを適切に生成するには、1つのパラメーターを受け取り、このパラメーターに依存する乱数を生成する関数が必要です。 つまり、同じパラメーター値の場合、出力には同じ番号が必要です。 GLSL標準ライブラリには、このような関数noise、noise2などへの参照が含まれていますが、実際にはどのメーカーによっても実装されていません（宿題：なぜ？）。したがって、最新版でも見られます。 したがって、独自のノイズを記述する必要があります。

従来のアプローチは次のとおりです。

 float hash(float x) { return fract(sin(x)*48737.3213); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、48737.3213は単なる数字で、数字キーパッドで猫と盲目的に入力しました。 インターネット上の人は、特定の番号をコピーして貼り付け、どこにでも一緒にドラッグするのが大好きですが、これについての説明は見ていません。

vec2からのノイズは、次の方法で取得できます。

 float hash(vec2 x) { return hash(dot(x,vec2(71.,313.))); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらの関数は、その名前が示すとおり、入力番号のハッシュのようなものであり、この数値がわずかに変化するだけで、それらの値は大幅に変化します。 この目的のためには、値がよりスムーズに変化する関数が必要です。 ハッシュに基づいたこのような関数を作成する方法はいくつかありますが、主なものはパーリンノイズ、バリューノイズ、シンプレックスノイズです。



今シーズンのインターネットでは、Perlinのノイズを間違えて、数オクターブのノイズの追加と考えるのが流行しています。 マルチオクターブノイズ、またはフラクタルノイズは、Perlinのノイズだけでなく、他のノイズにも基づいた完全に独立した手法です。 パーリンのノイズは、N次元グリッドを取得し、そのノードにランダムな正規化勾配を配置するという事実（=正規化されたランダムベクトル）に基づいています。その後、空間の各ポイントについて、グリッドのボリュームで、スカラー積を計算できますすべてのノードおよびこれらの製品間でN線形補間します。 線形補間は、より複雑な補間に置き換えることができます。たとえば、何らかの理由で必要に応じて、結果のノイズの2次導関数を滑らかにすることができます。 これはパーリンのノイズです。 かさばってかっこいいです。 この2分間の教育プログラムの後、今度は他のすべての人を笑って鼻を上げることもできます。





ここでは、シンプレックスノイズとペルリンノイズを使用しません。計算が複雑すぎるためです。 宇宙を奴隷化するというささやかな目標のために、値ノイズで十分です-グリッドノードでランダムな値を取得し、次のようにそれらの間を補間します。

 //  value noise float noise(vec2 x) { // F -    , f -   vec2 F = floor(x), f = fract(x); //   vec2 e = vec2(1.,0.); //  f *= f * (3. - 2. * f); //   return mix( mix(hash(F+e.yy), hash(F+e.xy), fx), mix(hash(F+e.yx), hash(F+e.xx), fx), fy); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

悪名高いフラクタルノイズは、数オクターブの単純な合計によって得られます。

 //   float fnoise(vec2 x) { //       x += vec2(10.); //   return .5 * noise(x) + .25 * noise(x*1.97) + .125 * noise(x*4.04) + .0625 * noise(x*8.17) ; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合計で、ノイズの視覚的な表現が得られます。



（ シークレットボーナストラック2 ）

すべてを破壊する

このランダム性のソースを使用すると、必要なことを何でも行うことができます。 たとえば、都市を描画します。

主なアイデア：スペースを4分の1セクターに分割し、セクターごとに、その座標番号を使用して、カオスから建物パラメーター（寸法、階数、タイプ）を抽出します。

同様に、たとえば、ウィンドウを強調表示できます。高さと位置に応じて乱数を取得し、それに基づいてこの「ウィンドウ」のライトがオンかどうかを決定します。

カメラの位置、星空-これもすべてランダムな値で箱から出ます。

一般に、私は実際にこの貧弱なテキストを書くのに疲れています。 おそらくあなたはそれを読むのにうんざりしているよりもさらに多くのことでしょう。 それでは、見てみましょう????? 利益を得て、もう寝ます！



注意、ビデオカードのスライドショー：

おわりに

この経済を縮小するために今も残っています-いくつかのコメントを削除し、変数と関数の名前を短くし、スペース、改行を削除し、フレームワークが2番目の部分に期待する種類にします（Sheydertoeの代わりに変数を挿入します）。 まあ、つまり、それは不可能です。なぜなら、それはまだ完全な悪趣味であり、プログラマーを常に倒すデザイナーが必要だからです。

一般的に、これは宿題です-このシェーダーを実行させて、エルフの重量を確認します。 私の予備的な見積もりは2..2.5Kbです。



最後の1つ：奇妙な偶然の一致により、今日（2013年10月21日月曜日）突然、講堂で19:30の夜にNSU（ノボシビルスク州立大学）で同じことについてさらに詳しく話します。 223の新しいスポーツ施設 。 あなたはすでにすべてを知っているので、あなたは来ないかもしれません、笑。 さて、それとは反対に、来て、私たちは救います！



前のシリーズ：Cプログラミング言語での音楽の合成。

次のシリーズ：おそらくOpenCLでリアルタイムに偏りのないパストレースポリゴンジオメトリ。