また、この方法では、コンパレータなどの外部の追加ツールを使用せずに、主電源の周波数を測定できます。 しかし、同時に、一時的なMKリソースまたは周波数測定の精度を犠牲にする必要があります。
実効値を測定することが重要なのはなぜですか。たとえば、平均値を直線化するなど、他の値は測定しません。 ほとんどの「中国語」電子電圧計は、平均整流値によって線間電圧を測定します。 測定手順は次のとおりです。電源電圧の期間中に、電圧振幅のN個の値を選択し、結果を合計(符号なし)、Nで除算(平均)した後、結果に係数を掛けます

指定された係数は、整流された平均値からの正弦波(!)信号の実効値の依存性を決定します。
この測定手法はシンプルで、マイクロコントローラの多くのリソース(一時リソースとメモリリソースの両方)を必要としません。 このような測定手法の主な欠点は、非正弦波信号の大きな測定誤差です。
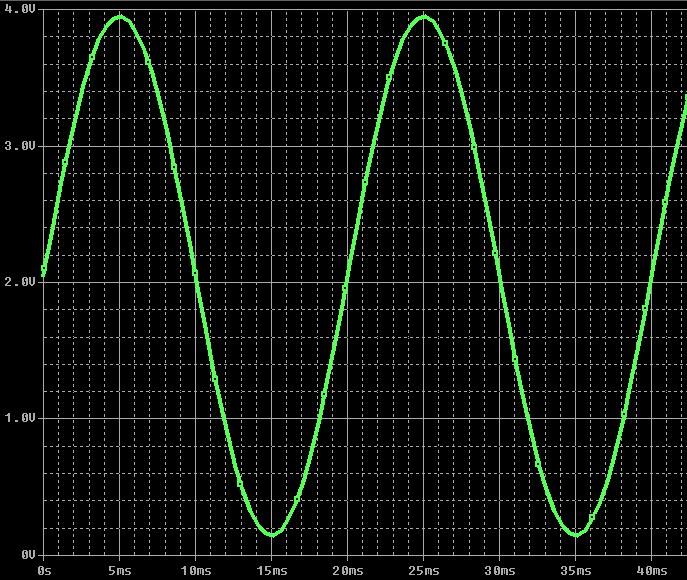
誰もが知っているように、電源電圧の信号の変化は正弦波の法則に従い(発電所で同期発電機を使用するため)、信号変化周波数は50 Hz(60 Hz)です。 ただし、実際には、外部要因(主に強力な非線形負荷をネットワークに接続する)の影響、および準正弦波出力電圧(図を参照)を持つインバーターの使用により、電圧正弦波は大幅に歪むか、矩形パルスに置き換えられます。 このような場合、上記の測定方法では非常に大きな誤差が生じます(たとえば、準正弦波インバーターでは、「中国語」電圧計で測定される出力電圧は180-200Vであり、有効電圧は220Vになります)。
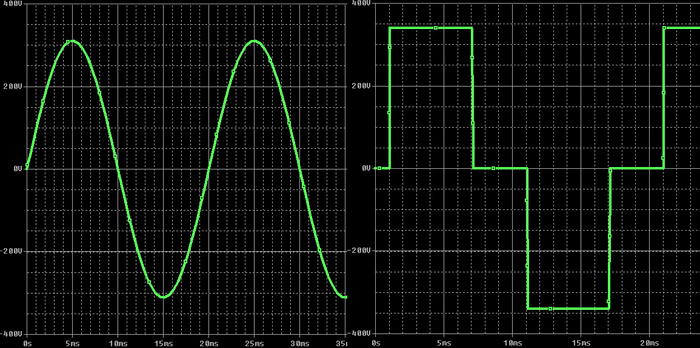
たとえば、私の家の緊張
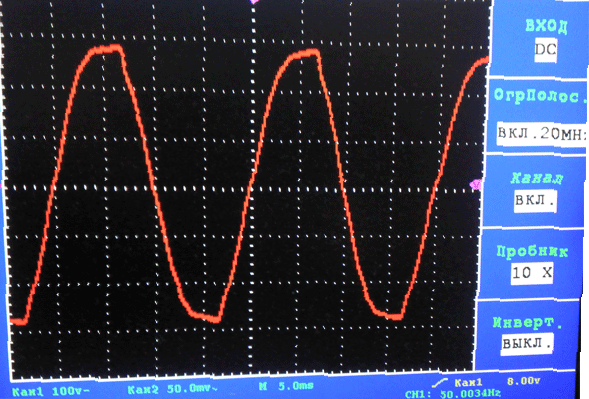
電圧(電流)の実際の値を測定することが重要なのはなぜですか? 電気システムの動作を決定するのは、電流(有効とも呼ばれる)電圧と電流値であるためです(大まかに言うと、電気ヒーターは、ネットワークの電圧と電流の電流値に正比例して熱を生成します)。
測定された周期値の実効値は、次の式で計算されます
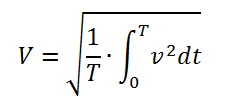
またはサンプリング後
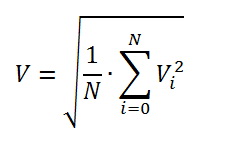
つまり 主電源電圧の周期に対していくつかの値を選択し、サンプルのポイントの平方の値を合計し、その期間のポイントの数で割って(サンプルポイントの数を決定するときは、コテルニコフ-シャノンの定理を忘れないでください)、結果の平方根を取る必要があります。
複雑ではないようですが、そうでない場合は:
1)各期間、サンプリングポイントが採用され、測定誤差が増加します。
2)電圧がゼロに近い実際のネットワークでは、「ゼロシェルフ」とゼロ電圧を介した繰り返し遷移の両方が発生する可能性があり、測定に大きな誤差が生じます。
各半周期のサンプルポイントの平方の合計を測定することにより、最初のポイントと格闘します。その後、(n + 1)番目からn番目の平方和を合計し、(n-1)番目をリクライニングします。
通常は両方向に5〜10 Vの電圧不感帯(正電圧側と負電圧側にゼロ電圧電圧境界を導入)、および周波数不感帯(許容電圧信号周波数を制限します)を導入することにより、2番目の段落と格闘します。
したがって、本線電圧の各半周期での期間の本線電圧の実効値の計算値を取得します。
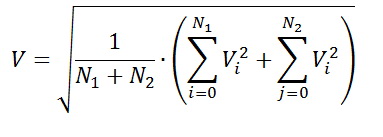
電圧の周波数は次の式で計算されます。

ここで、Fdはサンプリング周波数です(便宜上、周波数測定の精度を高めるために、10 kHz(サンプリング周期-100μs)に等しく選択されました)。
ここで、測定部分の構造図を検討します(実際の回路では、フィルタリング要素と保護要素を追加する必要があります)。
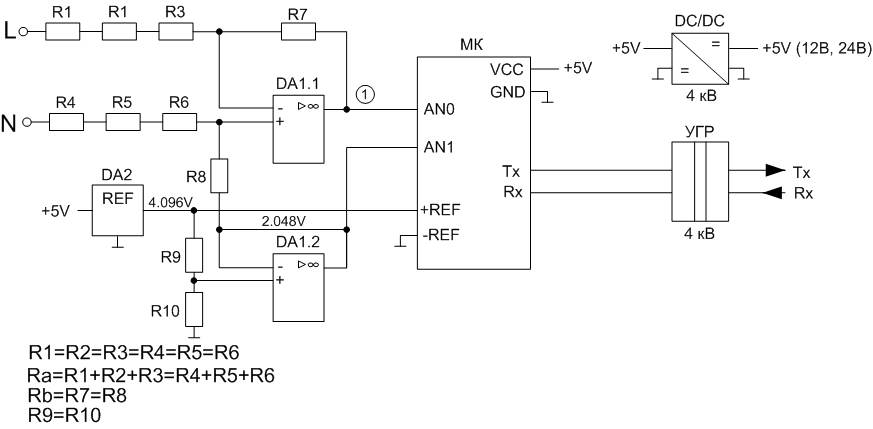
注意! この測定方法では、ネットワークからのマイクロコントローラのガルバニック絶縁は実装されていません。 マイクロコントローラからデータを送信するために、ガルバニック絶縁がデジタルインターフェースの側面に実装されています。
入力には、基準電圧の半分(2.048 V)でサポートされる分圧器を備えた差動オペアンプがあります。 サイズを小さくするには、低電力抵抗を使用することをお勧めします。少なくとも3個は取り付けてください。 抵抗が等しい-抵抗器の総絶縁破壊電圧を増加させます。 この場合、抵抗の許容電力を超えないように、最大入力電圧(P = U ^ 2 / R)での電力損失を計算する必要があります。 差動アンプの肩も等しくします。 次に、ポイント1の電圧は次の式で計算されます。
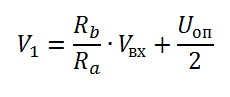
そして、ポイント1の電圧は次の形式になります。
また、基準電圧の半分がADCチャネルの1つに供給されます。 これにより、測定された電圧のゼロレベルの位置を決定するために、連続的に(たとえば、1周期に1回)決定することができます。
つまり ユニポーラパワーアンプで管理し、ポイント1の入力信号は0からUopに変化します。 この方法は、たとえばダイオードを使用した電圧整流と比較して、かなり正確な結果を提供します。
ADCの分周器と係数の計算は次のとおりです。

ここで、AおよびBは、現在および前の半周期のADC測定値(測定された信号ゼロ値-AN1)です。 N1、N2-現在および前の半周期の測定数。 Nad-ADCビット深度。 U'opは、基準電圧からオペアンプの非直線性(非感度)ゾーンを引いたものです(通常0.6 V)。
正弦波ではなく、正弦波の振幅に縮小された信号定数を考慮して、分周器を計算すると便利です。 次に、信号の実効値は振幅に等しく、各測定値に等しくなります。
たとえば、AC 420Vの最大値を測定するには、分周器を計算する必要があります。

抵抗Raは、500 kOhm〜1500 kOhmの範囲で選択されます。 選択した抵抗Raに基づいて、Rbが計算されます。
その結果、電圧と周波数の実効値を計算するアルゴリズムは次の形式を取ります。
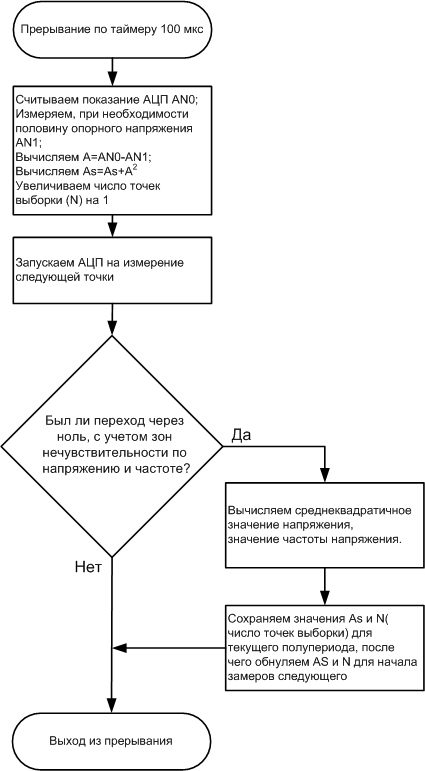
同時に、高価な計算(除算、ルート抽出)の一部を割り込みからメインプログラムに転送できます。
8ビットMKで有効な値を計算する場合、浮動小数点計算に頼らずに整数法(スケールファクターを使用)を使用し、可能であれば算術演算(除算、平方根の削除など)を簡素化することをお勧めします。 これにより、MKリソースが大幅に節約されます。