Clever Geek Handbook

自己組織化インクリメンタルニューラルネットワーク（SOINN）アルゴリズム

はじめに



教師なしで教えるタスクの1つは、入力データの分布のトポロジを最も正確に反映するトポロジ構造を見つけるタスクです。 この問題を解決するには、いくつかのアプローチがあります。 たとえば、 Kohonen Self-Organizing Mapsアルゴリズムは、多次元空間を、定義済みの構造を持つ低次元（通常は2次元）の空間に投影する方法です。 元の問題の次元の縮小と所定のネットワーク構造により、投影欠陥が発生しますが、その分析は困難な作業です。 このアプローチの代替手段の1つとして、Hebbの競争力のあるトレーニングと神経ガスの組み合わせは、トポロジ構造の構築により効果的です。 しかし、このアプローチの実際の適用は多くの問題によって妨げられています：必要なネットワークサイズの事前知識とこのネットワークへのトレーニングレート適応方法の適用の難しさが必要です、過剰な適応は新しいデータを学習するときの効率の低下につながり、適応速度が遅すぎるとノイズの多いデータに対する感度が高くなります。



オンライントレーニングまたは長期トレーニングのタスクには、上記の方法は適していません。 このようなタスクの基本的な問題は、既知の情報を損傷または破壊することなく、システムが新しい情報に適応する方法です。



この記事では、上記の問題を部分的に解決するSOINNアルゴリズムについて説明します。





検討中のアルゴリズムの概要



教師なしで教えるタスクでは、量を事前に知らなくても、入ってくるデータをクラスに分割する必要があります。 また、ソースデータのトポロジを決定する必要があります。



そのため、アルゴリズムは次の要件を満たしている必要があります。





SOINNは2つの層を持つニューラルネットワークです。 最初のレイヤーを使用してクラスターのトポロジ構造を決定し、2番目のレイヤーを使用してクラスターの数を決定し、クラスターのプロトタイプノードを特定します。 まず、ネットワークの第1層がトレーニングされ、次に、第1層のトレーニング中に取得されたデータを使用して、ネットワークの第2層がトレーニングされます。



教師なしの分類タスクの場合、入力画像が以前に取得したクラスターの1つに属するか、新しいクラスターを表すかを判断する必要があります。 2つの画像が同じクラスターに属し、それらの間の距離（所定のメトリックによる）が距離のしきい値Tより小さい場合、Tが大きすぎる場合、すべての入力画像は同じクラスターに割り当てられます。 Tが小さすぎる場合、各イメージは個別のクラスターとして分離されます。 合理的なクラスター化を実現するには、Tはクラス内距離よりも大きく、クラス間距離よりも小さくなければなりません。



SOINNネットワークの各レイヤーについて、しきい値Tを計算する必要があります。最初のレイヤーにはソースデータの構造に関する先験的な知識がないため、Tは既に構築されたネットワークの構造と現在の入力画像の知識に基づいて適応的に選択されます。 2番目のレイヤーをトレーニングするとき、クラス内およびクラス間の距離を計算し、しきい値Tの定数値を選択できます。



トポロジー構造を表すために、オンラインまたは生涯学習タスクでは、ネットワークの成長はエラーを減らし、古いデータを維持しながら変化する条件に適応するための重要な要素です。 しかし同時に、ノード数の制御されない増加は、ネットワークの混雑と全体としての「再トレーニング」につながります。 したがって、ネットワークに新しいノードを追加する時期と方法、および新しいノードの追加を禁止する時期を決定する必要があります。



ノードを追加するために、SOINNは挿入が最大エラーで領域で発生するスキームを使用します。 また、挿入物の有用性を評価するために、「誤差半径」が使用されます。これは、挿入物の有用性の推定値です。 この評価により、挿入によってエラーが削減され、ノードの成長が制御され、最終的にノードの数が安定します。



ニューロン間の接続を確立するために、トポロジー分布ネットワーク（TRN）でMartinezによって提案されたHebb競合ルールが使用されます。 ヘブの競合ルールは次のように説明できます。各入力信号について、2つの最も近いノードが結合されます。 各グラフが入力データのトポロジを最適に表していることが証明されています。 オンラインまたは生涯学習タスクでは、ノードの位置はゆっくりですが、絶えず変化します。 したがって、早い段階で隣接するノードは、後の段階で近くない場合があります。 このため、最近更新されていない接続を削除する必要があります。



一般的な場合、既存のクラスターの重複も発生します。 クラスターの数を正確に決定するために、入力データは分離可能であると想定されています。各クラスターの中央部分の確率密度はクラスター間の部分の密度よりも高く、クラスターの重なりは低い確率密度です。 クラスターからの分離は、確率密度が低い領域からノードを削除することで発生します。 SOINNアルゴリズムは、確率密度が低い領域からノードを削除するために次の戦略を提供します：これまでに生成された信号の数が特定のパラメーターの整数倍である場合、トポロジの近傍が1つしかない、または近傍がまったくないノードを削除し、ローカルに累積される場合信号レベルが小さいため、このようなノードは確率密度の低い領域にあると見なし、削除します。



アルゴリズムの説明



さて、上記に基づいて、SOINNネットワークの学習アルゴリズムの形式的な説明を行うことができます。 このアルゴリズムは、ネットワークの第1層と第2層の両方をトレーニングするために使用されます。 唯一の違いは、第2層をトレーニングするための入力が第1層によって生成されることであり、第2層をトレーニングする場合、一定の類似性しきい値を計算するために第1層のトポロジ構造がわかります。



使用される表記







アルゴリズム



  1. 2つのノードc1とc2でノードAのセットを初期化します。

    A = {c1、c2}

    空のセットでエッジCのセットを初期化します。

    C = {}。
  2. R ^ nから新しい信号xを入力します。
  3. 勝者s1とセットAの2番目の勝者のノードを、最も近いおよび次の重みベクトル（特定のメトリックによる）を持つノードとして見つけます。 x、s1、およびs2の間の距離が類似性しきい値Ts1またはTs2より大きい場合、新しいノードを作成して手順2に進みます。
  4. s1とs2の間のエッジが存在しない場合は、作成します。 それらの間のエッジ経過時間を0に設定します。
  5. s1から出現するすべてのアークの年齢を1つ増やします。
  6. 入力信号と勝者の間の距離をローカル総誤差Es1に追加します。
  7. ノードs1のローカル信号数を増やします。

    Ms1 = Ms1 +1
  8. 勝者と彼の直接のトポロジカルネイバーの重みベクトルを調整します。

    Ws1 = Ws1 + e1（t）（x-Ws1）

    Wsi = Wsi + e2（t）（x-Wsi）

    ここで、e1（t）およびe2（t）は、勝者とその隣人の学習因子です。
  9. 指定したしきい値を超える年齢のエッジを削除します。
  10. これまでに生成された入力信号の数がラムダパラメーターの倍数である場合、新しいノードを挿入し、次の規則に従って確率密度の低い領域のノードを削除します。

    1. 最大エラーのあるノードqを見つけます。
    2. 近傍qの中で最大誤差を持つノードfを見つけます。
    3. ノードrを追加して、その重みベクトルが重みqとfの算術平均になるようにします。
    4. 累積誤差Er、信号の総数Mr、および継承された誤差半径を計算します。

      Er = alpha1 *（Eq + Ef）

      Mr = alpha2 *（Mq + Mf）

      Rr = alpha3 *（Rq + Rf）
    5. ノードqおよびrの合計誤差を減らします。

      Eq =ベータ* Eq

      Ef =ベータ* Ef
    6. 累積信号数を減らします。

      Mq =ガンマ* Mq

      Mf =ガンマ* Mf
    7. 新しいノードの挿入が成功したかどうかを判断します。 挿入によってこのエリアの平均エラーを減らすことができない場合、挿入は失敗しました。 追加された頂点が削除され、すべてのパラメーターが元の状態に戻ります。 それ以外の場合、挿入に関係するすべてのノードのエラー半径を更新します。

      Rq = Eq / Mq

      Rf = Ef / Mf

      Rr = Er / Mr.
    8. 挿入が成功した場合、q <-> rおよびr <-> fリンクを作成し、q <-> fリンクを削除します。
    9. Aのすべてのノードの中から、1つだけの近傍を持つノードを見つけ、入力信号の累積数をすべてのノードの平均値と比較します。 ノードに含まれるネイバーが1つだけで、シグナルカウンターが適応しきい値を超えない場合は、ノードのセットから削除します。 たとえば、Li = 1でMi <c * sum_ {j = 1 ... Na} Mj / Na（ここで0 <c <1）の場合、頂点iを削除します。
    10. すべての分離されたノードを削除します。
  11. 長い間、LT、入力データからの各クラスは、構築されたグラフに接続されたコンポーネントを持ちます。 クラスラベルを更新します。
  12. ステップ2に進み、トレーニングを続けます。




しきい値計算アルゴリズム



第1層の場合、類似性しきい値Tは、次のアルゴリズムによって適応的に計算されます。

  1. 新しいノードの類似性しきい値を+ ooに初期化します。
  2. ノードが最初または2番目の勝者である場合、類似性しきい値を更新します。

    1. ノードに直接のトポロジネイバーがある場合（Li> 0）、ノードとそのネイバー間の最大距離としてTiの値を更新します。

      Ti =最大|| Wi-Wj ||
    2. ノードに隣接ノードがない場合、TiはノードとセットA内の他のノードとの間の最小距離として設定されます。

      Ti =分|| Wi-Wc ||


2番目のレイヤーでは、類似性のしきい値は一定であり、次のように計算されます。

  1. クラス内距離を計算します。

    dw = 1 / Nc * sum _ {（i、j）in C} || Wi-Wj ||
  2. クラス間距離を計算します。 クラスCiとCjの間の距離は、次のように計算されます。

    db（Ci、Cj）= max_ {Ciのi、Cjのj} || Wi-Wj ||
  3. 類似度しきい値Tcとして、クラス内距離を超える最小クラス間距離を取ります。




アルゴリズムの概略図





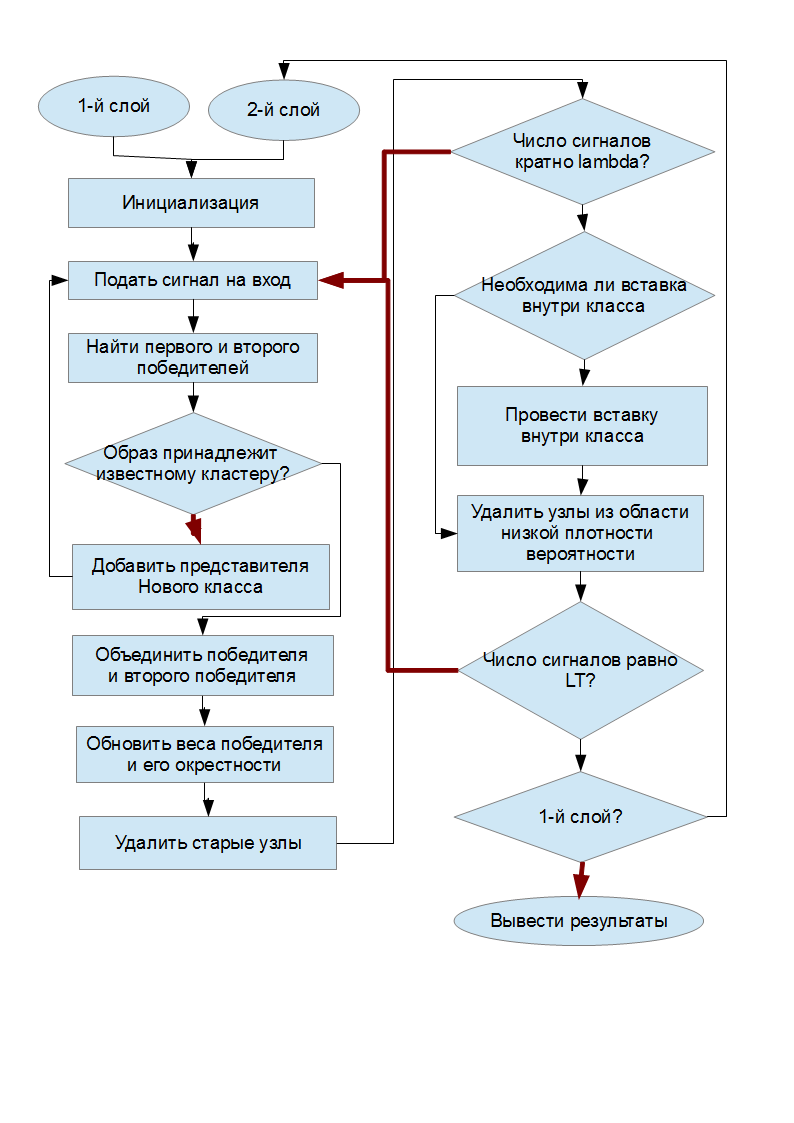
「条件付き」ダイヤモンドでは、黒い矢印は条件の履行に対応し、赤い矢印は履行されないことに対応します。



実験



このアルゴリズムで実験を行うために、Boost Graph Libraryを使用してC ++で実装しました。 コードはここからダウンロードできます 。



実験では、次のアルゴリズムパラメータが選択されました。

  1. ラムダ= 100
  2. age_max = 100
  3. c = 1.0
  4. alpha1 = 0.16
  5. alpha2 = 0.25
  6. alpha3 = 0.25
  7. ベータ= 0.67
  8. ガンマ= 0.75




2つのクラス（リングと円）を表す次の画像をテストデータとして使用しました。



これらのクラスから20,000個のランダムに取得したポイントをSOINNネットワークの入力に適用した後、次の形式の最初のネットワーク層が形成されました。



第1層で得られたデータに基づいて、次の形式の第2層が形成されました。





結論



この記事では、データ謝罪に基づく教師なし学習アルゴリズムの1つを検討しました。 実験的に得られた結果から、この方法の適用は公正であると結論付けることができます。

それでも、SOINNアルゴリズムの欠点に注目する価値はあります。

  1. ネットワークレイヤーは次々と順番にトレーニングされるため、第1レイヤーのトレーニングを停止して第2レイヤーのトレーニングを続行する価値がある瞬間を判断することは困難です。
  2. ネットワークの最初のレイヤーを変更する場合、2番目のレイヤーを完全に再トレーニングする必要があります。 この点で、オンライン学習の問題は解決されていません。
  3. ネットワークには、手動で選択する必要のある多くのパラメーターがあります。




中古文学



「オンライン教師なし分類およびトポロジ学習のためのインクリメンタルネットワーク」Fur尾S、長谷川修、2005年


More articles:


All Articles