🧘🏿 ⚾️ 🎦 数独生成アルゴリズム 🤲🏼 👛 🕞

良い一日！

数独パズルを紹介する必要はないと思います。私たちの多くは彼女の決定の背後に多くの時間を費やしています。たとえば、道路で時間をつぶしたり、脳が乾かないように頭を回転させる必要がある場合。ハブには、パズルを解くための非常に多くの投稿があります。しかし、人が1ダース、または多分100パズルを解くと、次の質問をする探究心が生まれます。また、9x9グリッドのアルゴリズムをどのように説明できますか？」

上記のアルゴリズムは非常に論理的です。しかし、私のタスクは、記述して実装することでした。これはすべてカットの下に書かれています。

基本的な数独ルール

番号は各行に一度だけ表示できます
番号は各列に一度だけ表示される場合があります
数字は各エリアに1回だけ表示できます（エリアは、3x3辺の小さな正方形で、下の画像で紫色に強調表示されています）

ステップ1.基本的なグリッドを基礎として

グリッドは数独規則に従う必要があります。最初の行1 2 ... 8 9に配置します。下の行では、左に3ポジションシフトします。 4 5 ... 2 3および7 8 ... 5 6。

さらに、次のエリアに垂直に移動して、前のエリアの左に1ポジション移動します。

最後に、このようなグリッドを取得する必要があります。これを基本グリッドと呼びます。

実装するには、グリッドクラスを作成します。テーブルがテーブル値のリストであるステップ1に従って入力します。showメソッドはテーブルの視覚的な出力です。

class grid: def __init__(self,n = 3): """Generation of the base table""" self.n = n self.table = [[((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)] print "The base table is ready!" def __del__(self): pass def show(self): for i in range(self.n*self.n): print self.table[i]

ステップ2.グリッドをシャッフルする

順列にはいくつかのタイプがあり、その後、数独テーブルは許容可能な状態になります。

これらには以下が含まれます。

テーブル全体を転置-列が行になり、逆も同様です（転置）

同じエリア内の2行の交換（ swap_rows_small ）
同じ領域内の2つの列を交換します（ swap_colums_small ）

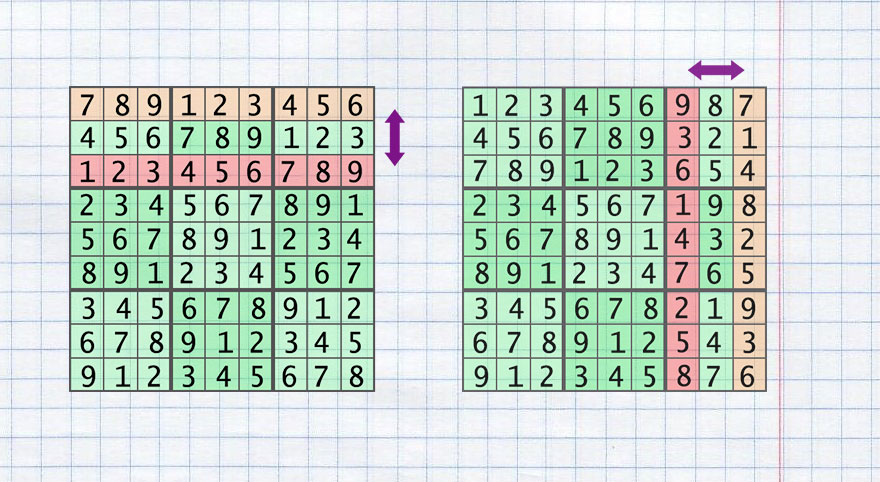
2つの領域の水平方向の交換（ swap_rows_area ）
2つの領域を垂直にスワップ （ swap_colums_area ）

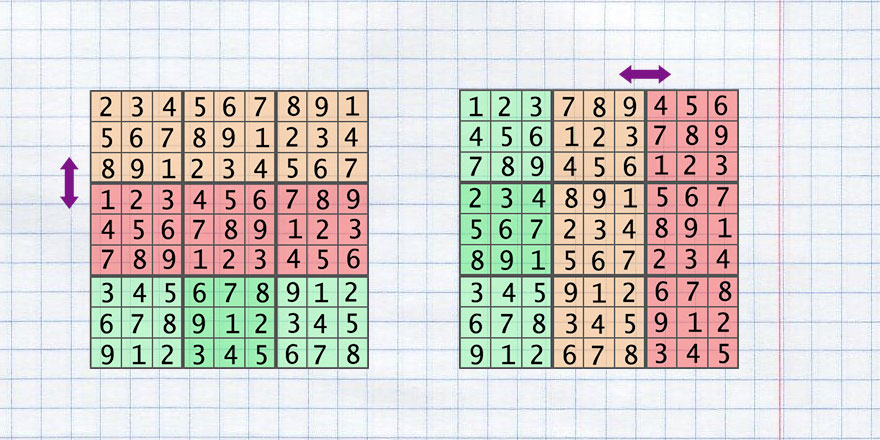
順列ごとに、メソッドを記述します。

転置

  def transposing(self): """ Transposing the whole grid """ self.table = map(list, zip(*self.table))

swap_rows_small

  def swap_rows_small(self): """ Swap the two rows """ area = random.randrange(0,self.n,1) line1 = random.randrange(0,self.n,1) #      N1 = area*self.n + line1 # 1    line2 = random.randrange(0,self.n,1) while (line1 == line2): line2 = random.randrange(0,self.n,1) N2 = area*self.n + line2 # 2    self.table[N1],self.table[N2] = self.table[N2], self.table[N1]

swap_colums_small

列を交換するには、転置されたテーブルの行を変更できます。

  def swap_colums_small(self): grid.transposing(self) grid.swap_rows_small(self) grid.transposing(self)

swap_rows_area

  def swap_rows_area(self): """ Swap the two area horizon """ area1 = random.randrange(0,self.n,1) #   area2 = random.randrange(0,self.n,1) while (area1 == area2): area2 = random.randrange(0,self.n,1) for i in range(0, self.n): N1, N2 = area1*self.n + i, area2*self.n + i self.table[N1], self.table[N2] = self.table[N2], self.table[N1]

swap_colums_area

  def swap_colums_small(self): grid.transposing(self) grid.swap_rows_area(self) grid.transposing(self)

さらに複雑な変換もあるかもしれませんが、これらに限定できると思います。このフレームワークはその構造が不変であり、そのような置換は、ルービックキューブの行列式または回転に関する行列のアクションとほとんど同じです。

ランダムな組み合わせを取得するには、シャッフル関数をランダムな順序で実行するだけです。やってみましょう、amtはミキシングの量です：

  def mix(self,amt = 10): mix_func = ['self.transposing()', 'self.swap_rows_small()', 'self.swap_colums_small()', 'self.swap_rows_area()', 'self.swap_colums_area()'] for i in xrange(1, amt): id_func = random.randrange(0,len(mix_func),1) eval(mix_func[id_func])

例10反復ミキシング

 base [1, 2, 3, 4, 5, 6, 7, 8, 9] [4, 5, 6, 7, 8, 9, 1, 2, 3] [7, 8, 9, 1, 2, 3, 4, 5, 6] [2, 3, 4, 5, 6, 7, 8, 9, 1] [5, 6, 7, 8, 9, 1, 2, 3, 4] [8, 9, 1, 2, 3, 4, 5, 6, 7] [3, 4, 5, 6, 7, 8, 9, 1, 2] [6, 7, 8, 9, 1, 2, 3, 4, 5] [9, 1, 2, 3, 4, 5, 6, 7, 8] swap_colums_area [7, 8, 9, 4, 5, 6, 1, 2, 3] [1, 2, 3, 7, 8, 9, 4, 5, 6] [4, 5, 6, 1, 2, 3, 7, 8, 9] [8, 9, 1, 5, 6, 7, 2, 3, 4] [2, 3, 4, 8, 9, 1, 5, 6, 7] [5, 6, 7, 2, 3, 4, 8, 9, 1] [9, 1, 2, 6, 7, 8, 3, 4, 5] [3, 4, 5, 9, 1, 2, 6, 7, 8] [6, 7, 8, 3, 4, 5, 9, 1, 2] swap_colums_small [7, 8, 9, 4, 5, 6, 2, 1, 3] [1, 2, 3, 7, 8, 9, 5, 4, 6] [4, 5, 6, 1, 2, 3, 8, 7, 9] [8, 9, 1, 5, 6, 7, 3, 2, 4] [2, 3, 4, 8, 9, 1, 6, 5, 7] [5, 6, 7, 2, 3, 4, 9, 8, 1] [9, 1, 2, 6, 7, 8, 4, 3, 5] [3, 4, 5, 9, 1, 2, 7, 6, 8] [6, 7, 8, 3, 4, 5, 1, 9, 2] swap_colums_small [7, 8, 9, 4, 5, 6, 1, 2, 3] [1, 2, 3, 7, 8, 9, 4, 5, 6] [4, 5, 6, 1, 2, 3, 7, 8, 9] [8, 9, 1, 5, 6, 7, 2, 3, 4] [2, 3, 4, 8, 9, 1, 5, 6, 7] [5, 6, 7, 2, 3, 4, 8, 9, 1] [9, 1, 2, 6, 7, 8, 3, 4, 5] [3, 4, 5, 9, 1, 2, 6, 7, 8] [6, 7, 8, 3, 4, 5, 9, 1, 2] transposing [7, 1, 4, 8, 2, 5, 9, 3, 6] [8, 2, 5, 9, 3, 6, 1, 4, 7] [9, 3, 6, 1, 4, 7, 2, 5, 8] [4, 7, 1, 5, 8, 2, 6, 9, 3] [5, 8, 2, 6, 9, 3, 7, 1, 4] [6, 9, 3, 7, 1, 4, 8, 2, 5] [1, 4, 7, 2, 5, 8, 3, 6, 9] [2, 5, 8, 3, 6, 9, 4, 7, 1] [3, 6, 9, 4, 7, 1, 5, 8, 2] swap_colums_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [4, 7, 1, 5, 8, 2, 3, 9, 6] [5, 8, 2, 6, 9, 3, 4, 1, 7] [6, 9, 3, 7, 1, 4, 5, 2, 8] [1, 4, 7, 2, 5, 8, 9, 6, 3] [2, 5, 8, 3, 6, 9, 1, 7, 4] [3, 6, 9, 4, 7, 1, 2, 8, 5] swap_rows_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] [1, 4, 7, 2, 5, 8, 9, 6, 3] [2, 5, 8, 3, 6, 9, 1, 7, 4] [3, 6, 9, 4, 7, 1, 2, 8, 5] swap_rows_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] [2, 5, 8, 3, 6, 9, 1, 7, 4] [1, 4, 7, 2, 5, 8, 9, 6, 3] [3, 6, 9, 4, 7, 1, 2, 8, 5] swap_rows_area [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [2, 5, 8, 3, 6, 9, 1, 7, 4] [1, 4, 7, 2, 5, 8, 9, 6, 3] [3, 6, 9, 4, 7, 1, 2, 8, 5] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] swap_colums_small [7, 1, 4, 8, 2, 5, 6, 9, 3] [8, 2, 5, 9, 3, 6, 7, 1, 4] [9, 3, 6, 1, 4, 7, 8, 2, 5] [2, 5, 8, 3, 6, 9, 1, 4, 7] [1, 4, 7, 2, 5, 8, 9, 3, 6] [3, 6, 9, 4, 7, 1, 2, 5, 8] [5, 8, 2, 6, 9, 3, 4, 7, 1] [4, 7, 1, 5, 8, 2, 3, 6, 9] [6, 9, 3, 7, 1, 4, 5, 8, 2]

ステップ3.細胞の除去

解決策を受け取った後、問題を解決する必要があります（この順序で解決策の一意性を保証できます）。そして、これは最も難しい部分です。独自のソリューションを保証するためにどれだけ削除できますか？これは、数独の複雑さが依存する重要な要素の1つです。数独には81個のセルがあり、通常はフィールドに30〜35個の「チップ」があり、中程度-25〜30個、難しい-20〜25個と考えられています。これは、実世界の例の大規模なセットからのデータです。複雑さに関する法律はありません。 30セルの不溶性バリアントと22セルの「ライト」を作成することができます。

ランダムなアプローチ -50〜60個のセルをランダムに投げることができますが、数独を解決できる確率はどこですか。たとえば、3行が入力された場合（= 27セル）
ちなみに単純な制限があります -たとえば、特定の数Nを制限として取ることができるため、N行と列は空になります。 N = 0-簡単なレベルの場合、N = 1-中、N = 2-難しい

それでは、セルの削除に進みましょう（すべてのオプションは同等であるため、取り消し可能な81個のセルがあるので、すべてを徹底的に検索して確認します）。

ランダムなセルNを選択
マークNを表示
Nを削除
決定を数えます。一意でない場合は、Nを返します

出力は、このミックスで可能な限り最も難しい数独になります。難しい変数は複雑さを評価します-残りの要素の数

 flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)] iterator = 0 difficult = example.n ** 4 #     while iterator < example.n ** 4: i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) #    if flook[i][j] == 0: #    iterator += 1 flook[i][j] = 1 # temp = example.table[i][j] #             example.table[i][j] = 0 difficult -= 1 #,    table_solution = [] for copy_i in range(0, example.n*example.n): table_solution.append(example.table[copy_i][:]) #    i_solution = 0 for solution in solver.solve_sudoku((example.n, example.n), table_solution): i_solution += 1 #   if i_solution != 1: #    --    example.table[i][j] = temp difficult += 1 # example.show() print "difficult = ",difficult

sudoku_generator.py

 # coding=utf-8 import random import solver class grid: def __init__(self,n = 3): """ Generation of the base table """ self.n = n self.table = [[ ((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)] print "The base table is ready!" def __del__(self): pass def show(self): for i in range(self.n*self.n): print self.table[i] def transposing(self): """ Transposing the whole grid """ self.table = map(list, zip(*self.table)) def swap_rows_small(self): """ Swap the two rows """ area = random.randrange(0,self.n,1) line1 = random.randrange(0,self.n,1) #      N1 = area*self.n + line1 # 1    line2 = random.randrange(0,self.n,1) # ,      while (line1 == line2): line2 = random.randrange(0,self.n,1) N2 = area*self.n + line2 # 2    self.table[N1],self.table[N2] = self.table[N2], self.table[N1] def swap_colums_small(self): grid.transposing(self) grid.swap_rows_small(self) grid.transposing(self) def swap_rows_area(self): """ Swap the two area horizon """ area1 = random.randrange(0,self.n,1) #   area2 = random.randrange(0,self.n,1) # ,      while (area1 == area2): area2 = random.randrange(0,self.n,1) for i in range(0, self.n): N1, N2 = area1*self.n + i, area2*self.n + i self.table[N1], self.table[N2] = self.table[N2], self.table[N1] def swap_colums_area(self): grid.transposing(self) grid.swap_rows_area(self) grid.transposing(self) def mix(self,amt = 10): mix_func = ['self.transposing()', 'self.swap_rows_small()', 'self.swap_colums_small()', 'self.swap_rows_area()', 'self.swap_colums_area()'] for i in xrange(1, amt): id_func = random.randrange(0,len(mix_func),1) eval(mix_func[id_func]) example = grid() example.mix() flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)] iterator = 0 difficult = example.n ** 4 #     example.show() print "---------------------------" while iterator < example.n ** 4: i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) #    if flook[i][j] == 0: #    iterator += 1 flook[i][j] = 1 # temp = example.table[i][j] #             example.table[i][j] = 0 difficult -= 1 #    table_solution = [] for copy_i in range(0, example.n*example.n): table_solution.append(example.table[copy_i][:]) #    i_solution = 0 for solution in solver.solve_sudoku((example.n, example.n), table_solution): i_solution += 1 #   if i_solution != 1: #       example.table[i][j] = temp difficult += 1 #  example.show() print "difficult = ",difficult

solver.py

 #!/usr/bin/env python3 # Author: Ali Assaf <ali.assaf.mail@gmail.com> # Copyright: (C) 2010 Ali Assaf # License: GNU General Public License <http://www.gnu.org/licenses/> from itertools import product def solve_sudoku(size, grid): """ An efficient Sudoku solver using Algorithm X. >>> grid = [ ... [5, 3, 0, 0, 7, 0, 0, 0, 0], ... [6, 0, 0, 1, 9, 5, 0, 0, 0], ... [0, 9, 8, 0, 0, 0, 0, 6, 0], ... [8, 0, 0, 0, 6, 0, 0, 0, 3], ... [4, 0, 0, 8, 0, 3, 0, 0, 1], ... [7, 0, 0, 0, 2, 0, 0, 0, 6], ... [0, 6, 0, 0, 0, 0, 2, 8, 0], ... [0, 0, 0, 4, 1, 9, 0, 0, 5], ... [0, 0, 0, 0, 8, 0, 0, 7, 9]] >>> for solution in solve_sudoku((3, 3), grid): ... print(*solution, sep='\\n') [5, 3, 4, 6, 7, 8, 9, 1, 2] [6, 7, 2, 1, 9, 5, 3, 4, 8] [1, 9, 8, 3, 4, 2, 5, 6, 7] [8, 5, 9, 7, 6, 1, 4, 2, 3] [4, 2, 6, 8, 5, 3, 7, 9, 1] [7, 1, 3, 9, 2, 4, 8, 5, 6] [9, 6, 1, 5, 3, 7, 2, 8, 4] [2, 8, 7, 4, 1, 9, 6, 3, 5] [3, 4, 5, 2, 8, 6, 1, 7, 9] """ R, C = size N = R * C X = ([("rc", rc) for rc in product(range(N), range(N))] + [("rn", rn) for rn in product(range(N), range(1, N + 1))] + [("cn", cn) for cn in product(range(N), range(1, N + 1))] + [("bn", bn) for bn in product(range(N), range(1, N + 1))]) Y = dict() for r, c, n in product(range(N), range(N), range(1, N + 1)): b = (r // R) * R + (c // C) # Box number Y[(r, c, n)] = [ ("rc", (r, c)), ("rn", (r, n)), ("cn", (c, n)), ("bn", (b, n))] X, Y = exact_cover(X, Y) for i, row in enumerate(grid): for j, n in enumerate(row): if n: select(X, Y, (i, j, n)) for solution in solve(X, Y, []): for (r, c, n) in solution: grid[r][c] = n yield grid def exact_cover(X, Y): X = {j: set() for j in X} for i, row in Y.items(): for j in row: X[j].add(i) return X, Y def solve(X, Y, solution): if not X: yield list(solution) else: c = min(X, key=lambda c: len(X[c])) for r in list(X[c]): solution.append(r) cols = select(X, Y, r) for s in solve(X, Y, solution): yield s deselect(X, Y, r, cols) solution.pop() def select(X, Y, r): cols = [] for j in Y[r]: for i in X[j]: for k in Y[i]: if k != j: X[k].remove(i) cols.append(X.pop(j)) return cols def deselect(X, Y, r, cols): for j in reversed(Y[r]): X[j] = cols.pop() for i in X[j]: for k in Y[i]: if k != j: X[k].add(i) if __name__ == "__main__": import doctest doctest.testmod()

作業結果

 The base table is ready! [5, 4, 6, 8, 7, 9, 2, 1, 3] [8, 7, 9, 2, 1, 3, 5, 4, 6] [2, 1, 3, 5, 4, 6, 8, 7, 9] [6, 5, 7, 9, 8, 1, 3, 2, 4] [9, 8, 1, 3, 2, 4, 6, 5, 7] [3, 2, 4, 6, 5, 7, 9, 8, 1] [7, 6, 8, 1, 9, 2, 4, 3, 5] [1, 9, 2, 4, 3, 5, 7, 6, 8] [4, 3, 5, 7, 6, 8, 1, 9, 2] --------------------------- [0, 0, 6, 0, 0, 0, 0, 0, 0] [8, 7, 0, 0, 1, 0, 0, 0, 6] [0, 0, 0, 5, 4, 0, 0, 0, 9] [6, 0, 0, 0, 8, 1, 3, 0, 4] [0, 0, 0, 3, 0, 0, 0, 5, 0] [0, 0, 0, 0, 0, 7, 0, 0, 0] [0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 9, 0, 4, 0, 0, 0, 0, 8] [0, 0, 5, 0, 6, 0, 1, 0, 0] difficult = 22

zipでダウンロード

数独テーブルを作成するためのより複雑なアプローチがあると確信しています。私の目標は達成され、実用的なアルゴリズムを得ました。今、私は新しいリリースを検索する必要はありません、それらを生成することができます:)

原則として、Sudoku 9x9の特別なケースがあります。ただし、16x16および25x25で使用する場合の制限はありません。

ソリューションを検証するために、アルゴリズムXが使用され、Sudoku向けに実装されました
すべての言語の数独ソリューションhttp://rosettacode.org/wiki/Sudoku

誰もが最高のお得な情報を持っている場合-コメントを残してお気軽に。

ご清聴ありがとうございました。

数独生成アルゴリズム