# Python
基本
おそらく、私が今まで聞いた中で、ダイナミクスの最高の説明を1つの文で書いたものです。
動的プログラミングとは、解決方法が明確ではないタスクがあり、それをより小さなタスクに分割することであり、これも解決方法が明確ではありません。 （c）A.クモック。
ダイナミクスによって問題を解決するには、次のものが必要です。
1）ダイナミクスの状態：サブタスクを一意に指定するパラメーター。
2）初期状態の値。
3）状態間の遷移：再計算式。
4）再集計の手順。
5）問題に対する答えの位置：これは時々合計、または、例えば、いくつかの状態の値の最大値です。
再計算手順
3つの変換オーダーがあります。
1）直接注文：
状態は、すでに計算された状態に基づいて順次再計算されます。
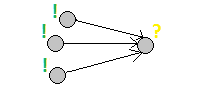
2）逆順：
現在の状態に応じて、すべてのステータスが更新されます。
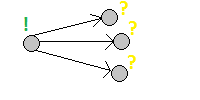
3）レイジーダイナミクス：
ダイナミクスの再帰的メモ再計算機能。 これは、エッジがそれらの間の依存関係である非循環状態グラフでのディープサーチのようなものです。
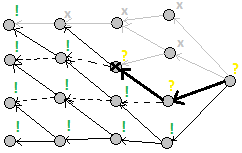
基本例： フィボナッチ数 ステータス-番号。
直接注文：
fib[1] = 1 # fib[2] = 1 # for i in range(3, n + 1): fib[i] = fib[i - 1] + fib[i - 2] # i
逆順：
fib[1] = 1 # for i in range(1, n): fib[i + 1] += fib[i] # i + 1 fib[i + 2] += fib[i] # i + 2
レイジーダイナミクス：
def get_fib(i): if (i <= 2): # return 1 if (fib[i] != -1): # return fib[i] fib[i] = get_fib(i - 1) + get_fib(i - 2) # return fib[i]
3つのオプションすべてに生命権があります。 それらはそれぞれ独自のスコープを持っていますが、多くの場合他のスコープと重複しています。
多次元ダイナミクス
1次元のダイナミクスの例は、上記の「変換の順序」で示されているため、すぐに多次元から始めます。 ご想像のとおり、1次元とは異なり、測定の数、つまり状態のパラメーターの数です。 これに基づく分類は通常、「1対2」スキームに基づいており、実際には特に基本的ではありません。
多次元ダイナミクスは1次元とそれほど変わりません。いくつかの例を見るとわかります。
例1：SMSの数
以前は、電話機にボタンがあった場合、キーボードは次のようになりました。
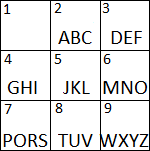
このようなキーボードのタップを
k
回以下使用して、複数のテキストメッセージをいくつ書くかを計算する必要があります。
解決策
1）ダイナミクス状態：
タップを使用した長さ
異なるメッセージの数。
2）初期状態：長さゼロのメッセージが1つあり、ゼロクリックを使用して-空。
3）再計算式：1回、2回、3回のクリックが必要な書き込み用の8文字と、4回のクリックが必要な2文字があります。
直接再集計：
4）変換手順：
直接書く場合、たとえば、小さな
は存在しないかもしれない
に向かうとき、ダイナミクスの境界を越えることについて別に考える必要があります。 これを回避するには、中立的な要素（答えを変更しない）に関してチェックを設定するか、書き留めます。
再集計を使用すると、すべてがよりシンプルになります。ネガティブな要素に陥らないように、常に前を向いています。
5）答えはすべての州の合計です。
UPD：
残念なことに、私は間違いを犯しました-状態からメッセージ
の長さを取り除くだけで、問題を1次元で解決できます。
1）ステータス：
回のクリックで入力できるさまざまなメッセージの数。
2）初期状態：
3）再計算式：
5）答えはすべての州の合計です。
dp[n][m]
m
タップを使用した長さ
n
異なるメッセージの数。
2）初期状態：長さゼロのメッセージが1つあり、ゼロクリックを使用して-空。
3）再計算式：1回、2回、3回のクリックが必要な書き込み用の8文字と、4回のクリックが必要な2文字があります。
直接再集計：
dp[n][m] = (dp[n - 1][m - 1] + dp[n - 1][m - 2] + dp[n - 1][m - 3]) * 8 + dp[n - 1][m - 4] * 2
カウントダウン：
dp[n + 1][m + 1] += dp[n][m] * 8 dp[n + 1][m + 2] += dp[n][m] * 8 dp[n + 1][m + 3] += dp[n][m] * 8 dp[n + 1][m + 4] += dp[n][m] * 2
4）変換手順：
直接書く場合、たとえば、小さな
m
は存在しないかもしれない
dp[n - 1][m - 4]
に向かうとき、ダイナミクスの境界を越えることについて別に考える必要があります。 これを回避するには、中立的な要素（答えを変更しない）に関してチェックを設定するか、書き留めます。
再集計を使用すると、すべてがよりシンプルになります。ネガティブな要素に陥らないように、常に前を向いています。
5）答えはすべての州の合計です。
UPD：
残念なことに、私は間違いを犯しました-状態からメッセージ
n
の長さを取り除くだけで、問題を1次元で解決できます。
1）ステータス：
dp[m]
m
回のクリックで入力できるさまざまなメッセージの数。
2）初期状態：
dp[0] = 1
3）再計算式：
dp[m] = (dp[m - 1] + dp[m - 2] + dp[m - 3]) * 8 + dp[m - 4] * 2
4）順序：3つのオプションすべてを使用できます。
5）答えはすべての州の合計です。
例2：馬
チェスの馬は、サイズ
N
x
M
ボード上のケージ
(1, 1)
に立っています
M
セル
(N, M)
に到達する方法の数を4つのタイプのステップでカウントする必要があります。
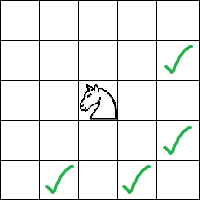
解決策
1）ダイナミクス状態：
-
に到達する方法の数。
2）初期値：セル
一方向で到達できます-何もしません。
3）再計算式：
直接注文の場合：
4）そして今、このタスクで最も興味深い部分は、順序です。 ここでは、行や列だけを移動することはできません。 それ以外の場合は、まだ再計算されていない状態を直接の順序で参照し、未完成の状態を逆のアプローチで取得するためです。
2つの方法があります。
1）適切な回避策を考え出します。
2）レイジーダイナミクスを実行し、彼女にそれを理解させます。
あなたが考えるのが面倒な場合-怠dynamicなダイナミクスを実行すると、それは完璧に仕事をします。
怠lazでなければ、次のような回避策を考えることができます。
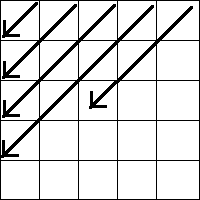
この順序により、直接ラウンドの各ステップで必要なすべてのセルの処理と、反対の現在の状態の処理が保証されます。
5）答えは単に
ます。
dp[i][j]
-
(i, j)
に到達する方法の数。
2）初期値：セル
(1, 1)
一方向で到達できます-何もしません。
3）再計算式：
直接注文の場合：
dp[i][j] = dp[i - 2][j - 1] + dp[i - 2][j + 1] + dp[i - 1][j - 2] + dp[i + 1][j - 2]
逆順の場合：
dp[i + 1][j + 2] += dp[i][j] dp[i + 2][j + 1] += dp[i][j] dp[i - 1][j + 2] += dp[i][j] dp[i + 2][j - 1] += dp[i][j]
4）そして今、このタスクで最も興味深い部分は、順序です。 ここでは、行や列だけを移動することはできません。 それ以外の場合は、まだ再計算されていない状態を直接の順序で参照し、未完成の状態を逆のアプローチで取得するためです。
2つの方法があります。
1）適切な回避策を考え出します。
2）レイジーダイナミクスを実行し、彼女にそれを理解させます。
あなたが考えるのが面倒な場合-怠dynamicなダイナミクスを実行すると、それは完璧に仕事をします。
怠lazでなければ、次のような回避策を考えることができます。
この順序により、直接ラウンドの各ステップで必要なすべてのセルの処理と、反対の現在の状態の処理が保証されます。
5）答えは単に
dp[n][m]
ます。
ダイナミクスと遷移マトリックス
行列を乗算したことがないが、この見出しを理解したい場合は、少なくともwikiを読む必要があります 。
例えば、永遠のフィボナッチ数など、動的計画法によってすでに解決した問題があると仮定します。
少し作り直しましょう。 ベクトルがありますか
。 数式を少し開いてみましょう。 
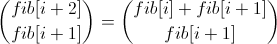。 あなたはベクトルからそれを見ることができます 
最初のベクトルの折り畳まれた変数のみが最終ベクトルに表示されるため、何らかの種類の行列を乗算します。 このマトリックスは簡単に導き出せます。ここにあります： 
。 これを遷移行列と呼びます。
これは、ベクトルを取る場合
遷移行列をn - 1
回乗算すると、ベクトルが得られます
、 fib[n]
-問題への答え。
そして今、なぜこれがすべて必要なのか。 行列の乗算には結合性の特性があります。
（しかし、これには可換性がありません。これは私の意見では驚くべきことです）。 このプロパティは、これを行う権利を与えます。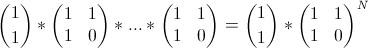 
。
これは、高速累乗法を適用できるためです。
。 合計で、算術演算の対数のN
フィボナッチ数を計算することができました。
そして今、例はより深刻です：
例3：ノコギリシーケンス
長さ
N
のこぎり波シーケンスを、極端でない各要素に対して条件が満たされるシーケンスとして示します。それは、その2つの近傍よりも小さいか、それ以上です。 長さ
N
の数字の鋸歯状シーケンスの数を計算する必要があります
N
次のようになります。
解決策
まず、遷移行列のないソリューション：
1）ダイナミクス状態：
-
桁で終わる長さ
のこぎり歯列の数。 そして、
場合、最後の桁は最後から2桁より小さく、
場合、それより大きくなります。
2）初期値：
たカップルのみです。
5）答えは合計
です。
ここで、初期ベクトルとそれに対応する遷移行列を作成する必要があります。 ベクトルはすぐに発明されたようです。すべての状態はシーケンス
長さを示します
さて、変換式を見て、遷移行列が導出されます。
1）ダイナミクス状態：
dp[n][last][less]
-
last
桁で終わる長さ
n
のこぎり歯列の数。 そして、
less == 0
場合、最後の桁は最後から2桁より小さく、
less == 1
場合、それより大きくなります。
2）初期値：
for last in range(10): dp[2][last][0] = 9 - last dp[2][last][1] = last
3）ダイナミクスの再計算：
for prev in range(10): if prev > last: dp[n][last][0] += dp[n - 1][prev][1] if prev < last: dp[n][last][1] += dp[n - 1][pref][0]
4）再計算の順序：常に以前の長さを参照するため、のネストさfor
たカップルのみです。
5）答えは合計
dp[N][0..9][0..1]
です。
ここで、初期ベクトルとそれに対応する遷移行列を作成する必要があります。 ベクトルはすぐに発明されたようです。すべての状態はシーケンス
N
長さを示します
N
さて、変換式を見て、遷移行列が導出されます。
ベクトルと遷移行列 
サブセグメントダイナミクス
これは、状態が配列のサブセグメントの境界であるダイナミクスクラスです。 一番下の行は、配列のすべての可能なサブセグメントに基づいてサブタスクの回答を計算することです。 通常、それらは長さの増加順にソートされ、計算はそれぞれ短いセグメントに基づいています。
例4：文字列のパック
これが展開された状態です。 簡単にもう一度言います。
圧縮された行を定義します。
1）文字のみで構成される文字列は、圧縮された文字列です。 彼女は自分自身を開きます。
2）2つの圧縮された文字列
A
と
B
連結した文字列 展開された行
A
と
B
を連結するために展開されます
B
3）文字列
D(X)
、ここで
D
は
1
より大きい整数、
X
は圧縮された文字列です。
X
から圧縮解除された
D
文字列の連結に圧縮解除されます
X
例：
“3(2(A)2(B))C”
“AABBAABBAABBC”
展開されます。
行
s
展開される最短の圧縮行の長さ
s
見つける必要があります。
解決策
この問題は、おそらく既に推測されているように、サブセグメントのダイナミクスによって解決されています。
1）ダイナミクス状態：
-文字列
展開される最小長の圧縮文字列
2）初期状態：長さ1のすべての部分文字列は、その中でのみ圧縮できます。
3）ダイナミクスの再計算：
最良の答えは、ある種の最終的な圧縮操作です。それは単に大文字の文字列であるか、2行の連結であるか、圧縮そのものです。 それでは、すべてのオプションを調べて、最適なものを選択しましょう。
5）答えは
ます。
1）ダイナミクス状態：
d[l][r]
-文字列
s[l:r]
展開される最小長の圧縮文字列
2）初期状態：長さ1のすべての部分文字列は、その中でのみ圧縮できます。
3）ダイナミクスの再計算：
最良の答えは、ある種の最終的な圧縮操作です。それは単に大文字の文字列であるか、2行の連結であるか、圧縮そのものです。 それでは、すべてのオプションを調べて、最適なものを選択しましょう。
dp_len = r - l dp[l][r] = dp_len # - . for i in range(l + 1, r): dp[l][r] = min(dp[l][r], dp[l][i] + dp[i][r]) # for cnt in range(2, dp_len): if (dp_len % cnt == 0): # , good = True for j in range(1, (dp_len / cnt) + 1): # , cnt good &= s[l:l + dp_len / cnt] == s[l + (dp_len / cnt) * j:l + (dp_len / cnt) * (j + 1)] if good: # cnt dp[l][r] = min(dp[l][r], len(str(cnt)) + 1 + dp[l][l + dp_len / cnt] + 1)
4）再カウントの手順：サブストリングの直接昇順または遅延ダイナミクス。
5）答えは
d[0][len(s)]
ます。
例5： オークス
サブツリーダイナミクス
サブツリーに沿ったダイナミクスの状態のパラメーターは、通常、この頂点がルートであるサブツリーを示す頂点です。 現在の状態の値を取得するには、通常、すべての子供の結果を知る必要があります。 ほとんどの場合、彼らはそれを遅延的に実装します-彼らは単に木の根から深さで検索を書きます。
例6：論理ツリー
中断されたツリーが与えられた場合、そのリーフにはシングルビット番号
0
または
1
が含まれます。 数値はすべての内部頂点にも書き込まれますが、次のルールに従って、各頂点に対して論理演算の1つが選択されます：「AND」または「OR」。 「AND」の場合、ピークの値はそのすべての子の値の論理「AND」です。 「OR」の場合、頂点の値はそのすべての子の値の論理「OR」です。
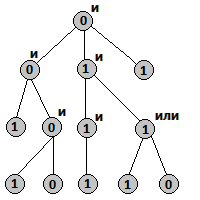
ルートの値が変更されるか、不可能であることを通知するように、内部頂点での論理演算の最小変更数を見つける必要があります。
解決策
1）ダイナミクス状態：
-頂点
で
の値を取得するために必要な操作の数。 これが不可能な場合、状態値は
です。
2）初期値：葉の場合、変更がゼロの場合に値を取得できることは明らかですが、値を変更することはできません。つまり、
操作に対してのみ可能です。
3）再計算式：
頂点の値がすでに
である場合、ゼロです。 そうでない場合、2つのオプションがあります。現在の頂点で操作を変更するかどうかです。 どちらの場合も、最適なオプションを見つけて最適なものを選択する必要があります。
「And」操作で「0」を取得する必要がある場合、答えは値
の最小値です。ここで、
は
の息子です。
「And」操作で「1」を取得する必要がある場合、答えはすべての値
の合計です。ここで、
は
の息子です。
操作が「OR」で、「0」を取得する必要がある場合、答えはすべての値
の合計です。ここで、
は
の息子です。
操作が「OR」で、「1」を取得する必要がある場合、答えは値
の最小値です。ここで、
は
の息子です。
4）再計算順序：最も簡単に遅延的に実装されます-ルートからの深さの検索の形式で。
5）答えは
です。
d[v][x]
-頂点
v
で
x
の値を取得するために必要な操作の数。 これが不可能な場合、状態値は
+inf
です。
2）初期値：葉の場合、変更がゼロの場合に値を取得できることは明らかですが、値を変更することはできません。つまり、
+inf
操作に対してのみ可能です。
3）再計算式：
頂点の値がすでに
x
である場合、ゼロです。 そうでない場合、2つのオプションがあります。現在の頂点で操作を変更するかどうかです。 どちらの場合も、最適なオプションを見つけて最適なものを選択する必要があります。
「And」操作で「0」を取得する必要がある場合、答えは値
d[i][0]
の最小値です。ここで、
i
は
v
の息子です。
「And」操作で「1」を取得する必要がある場合、答えはすべての値
d[i][1]
の合計です。ここで、
i
は
v
の息子です。
操作が「OR」で、「0」を取得する必要がある場合、答えはすべての値
d[i][0]
の合計です。ここで、
i
は
v
の息子です。
操作が「OR」で、「1」を取得する必要がある場合、答えは値
d[i][1]
の最小値です。ここで、
i
は
v
の息子です。
4）再計算順序：最も簡単に遅延的に実装されます-ルートからの深さの検索の形式で。
5）答えは
d[root][value[root] xor 1]
です。
サブセットダイナミクス
サブセット上のダイナミクスでは、特定のセットのマスクが通常状態になります。 それらは、このマスクのユニット数が増加する順序で最も頻繁に選択され、包含の小さい状態からそれぞれ再カウントされます。 回避策を特に考えないように、通常は怠dynamicなダイナミクスが使用されますが、これは完全に些細なことではありません。
例7：最小重量のハミルトニアンサイクル、または巡回セールスマン問題
サイズ
N
重み付き（エッジの重みが負でない）グラフ
G
与えられた場合 最小重みのハミルトニアンサイクル （自己交差なしですべての頂点を通過するサイクル）を見つけます。
解決策
すべての頂点を通過するサイクルを探しているので、「初期」頂点に任意のものを選択できます。 それを頂点番号
ます。
1）ダイナミクス状態：
-頂点
から頂点
までの最小重みのパス。
あり、それらに沿っているすべての頂点を通過します。
2）初期値：
、最初は他のすべての状態-
。
3）再計算式：
のi番目のビットが
、
から
へのエッジがある場合：
は
から
までのエッジの重みです。
4）変換手順：最も簡単で最も便利な方法は、レイジーダイナミクスを記述することですが、マスクの列挙を歪めて記述して、その中の単一ビットの数を増やすことができます。
5）答えは
ます。
0
ます。
1）ダイナミクス状態：
dp[mask][v]
-頂点
0
から頂点
v
までの最小重みのパス。
mask
あり、それらに沿っているすべての頂点を通過します。
2）初期値：
dp[1][0] = 0
、最初は他のすべての状態-
+inf
。
3）再計算式：
mask
のi番目のビットが
1
、
i
から
v
へのエッジがある場合：
dp[mask][v] = min(dp[mask][v], dp[mask - (1 << i)][i] + w[i][v])
ここで、 w[i][v]
は
i
から
v
までのエッジの重みです。
4）変換手順：最も簡単で最も便利な方法は、レイジーダイナミクスを記述することですが、マスクの列挙を歪めて記述して、その中の単一ビットの数を増やすことができます。
5）答えは
d[(1 << N) - 1][0]
ます。
プロファイルダイナミクス
プロファイルに沿ったダイナミクスによって解決される古典的な問題は、いくつかの数字でフィールドを並べるタスクです。 さらに、たとえば、タイリングの方法の数、または最小数の数字でタイリングするなど、さまざまなことが求められる場合があります。
これらのタスクは、
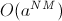ここでa
は1つのセルのタイリングのバリアントの数です。 プロファイルに沿ったダイナミクスは、いずれかの次元の時間を線形に最適化し、係数のみを指数関数的に残します。 次のようなものが得られます。
プロファイルは
k
列（多くの場合1列）で、既にタイル化されている部分とまだタイル化されていない部分との境界です。 この境界は部分的にしか塗りつぶされていません。 非常に多くの場合、ダイナミクスの状態の一部です。
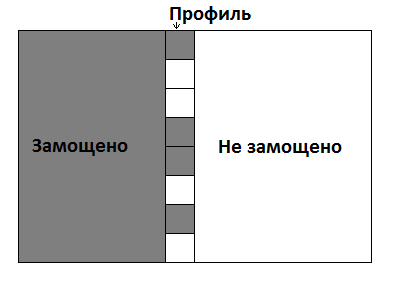
ほとんどの場合、状態はプロファイルであり、このプロファイルの場所です。 そして、移行により、この場所が1つ増えます。 プロファイルサイズに比例した時間で、あるプロファイルから別のプロファイルに切り替えることができるかどうかを確認できます。 これは再カウント中に毎回確認できますが、カウントすることもできます。 2次元配列
can[mask][next_mask]
をカウントします。複数の図形を配置して、プロファイルの位置を1つずつ増やすことで、あるマスクから別のマスクに移動できます。 カウントすると、実行時間が短くなり、メモリが増えます。
例8：ドミノの支配
1
x
2
および
2
x
1
寸法のドミノを使用して、テーブル
N
x
M
をブリッジする方法の数を見つけます。
解決策
ここでは、プロファイルは単一の列です。
タイル化されていない列セル、
タイル化されたバイナリマスクの形式で保存すると便利です。 つまり、合計プロファイル
。
0）事前計算（オプション）：プロファイルのすべてのペアを反復処理し、あるプロファイルから別のプロファイルに移行できることを確認します。 このタスクでは、これは次のように検証されます。
次の場所の最初のプロファイルが1の場合、2番目のプロファイルでは
でなければなりません
これは、このセルを数字で埋めることができないためです。
次の場所の最初のプロファイルが
場合、2番目の
または
2つのオプションがあります。
場合、これは垂直ドミノを配置する義務があることを意味します。つまり、次のセルを
と見なすことができます。
場合、垂直ドミノを配置し、次のセルに移動します。
遷移の例（上のプロファイルから下の遷移に移動できます）
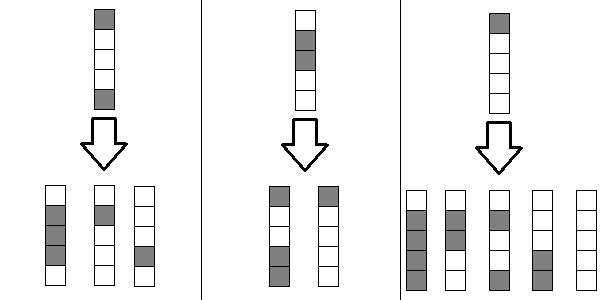
その後、すべてを配列に保存
、行くことができる場合、
できない場合。
1）ダイナミクスの状態：
-最初の
完全なタイルの数
プロファイル
列。
2）初期状態：
フィールドの左の境界は直線の壁です。
3）再計算式：
4）バイパス順
の増加順。
5）答えはdp [pos] [0]にあります。
結果の漸近は
。
0
タイル化されていない列セル、
1
タイル化されたバイナリマスクの形式で保存すると便利です。 つまり、合計プロファイル
。
0）事前計算（オプション）：プロファイルのすべてのペアを反復処理し、あるプロファイルから別のプロファイルに移行できることを確認します。 このタスクでは、これは次のように検証されます。
次の場所の最初のプロファイルが1の場合、2番目のプロファイルでは
0
でなければなりません
0
これは、このセルを数字で埋めることができないためです。
次の場所の最初のプロファイルが
0
場合、2番目の
0
または
1
2つのオプションがあります。
0
場合、これは垂直ドミノを配置する義務があることを意味します。つまり、次のセルを
1
と見なすことができます。
1
場合、垂直ドミノを配置し、次のセルに移動します。
遷移の例（上のプロファイルから下の遷移に移動できます）
その後、すべてを配列に保存
can[mask][next_mask]
1
、行くことができる場合、
0
できない場合。
1）ダイナミクスの状態：
dp[pos][mask]
-最初の
pos - 1
完全なタイルの数
pos - 1
プロファイル
mask
pos - 1
列。
2）初期状態：
dp[0][0] = 1
フィールドの左の境界は直線の壁です。
3）再計算式：
dp[pos][mask] += dp[pos - 1][next_mask] * can[mask][next_mask]
4）バイパス順
pos
の増加順。
5）答えはdp [pos] [0]にあります。
結果の漸近は
。
壊れたプロファイルダイナミクス
これは、プロファイルのダイナミクスの非常に強力な最適化です。 ここでは、プロファイルはマスクだけでなく、骨折部位でもあります。 次のようになります。
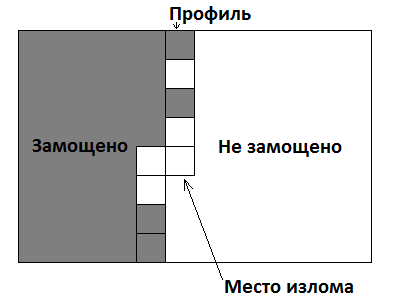
これで、プロファイルにキンクを追加した後、キンクの左のセルをカバーする1つの図のみを追加して、次の状態に進むことができます。 つまり、状態数を
N
倍に増やすことで（ブレークがどこにあるかを覚えておく必要があります）、1つの状態から別の状態への遷移の数を減らします。
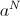前に 
。 漸近性の改善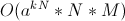 
。
ドミノのタイル張りの問題の例（例8）による、破損したプロファイルに沿ったダイナミクスの遷移：
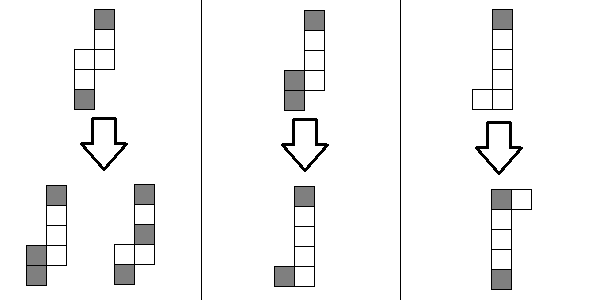
回答の回復
ベストアンサーの特性を知るだけでは不十分な場合があります。 たとえば、「文字列のパッキング」タスク（例4）では、圧縮された最短の文字列の長さだけで終わりますが、ほとんどの場合、その長さではなく、文字列自体が必要です。 この場合、答えを復元する必要があります。
各タスクには答えを復元する独自の方法がありますが、最も一般的な方法は次のとおりです。
- ダイナミクス状態の値の横に、サブタスクへの完全な応答を保持します。 答えが大きい場合、必要なメモリが多すぎる可能性があります。そのため、別の方法を使用できる場合、通常はそうします。
- 与えられた条件の祖先を知って、答えを復元します。 多くの場合、受け取った方法だけを知って、答えを復元できます。 同じ「ラインパッキング」で、答えを復元するために、最後のアクションのフォームとそれが受信された状態のみを保存できます。
- 追加のメモリをまったく使用しない方法があります-ダイナミクスを再計算した後、最後から最適なパスに進み、道に沿って答えを書きます。
マイナーな最適化
記憶
多くの場合、ダイナミクスでは、状態がカウントされる他の状態を非常に多く必要としないという問題に対処できます。 たとえば、フィボナッチ数を計算するとき、最後の2つだけを使用し、前の数に戻ることはありません。 したがって、それらについては忘れることができます。つまり、メモリに保存しないでください。 これにより、漸近的メモリ推定が改善される場合があります。 この手法は、例1、2、3（遷移マトリックスなしのソリューション）、7、8で使用できます。 確かに、バイパスの順序が遅延ダイナミクスの場合、これはまったく機能しません。
時間
ある種のデータ構造を使用して漸近時間を改善できる場合があります。 たとえば、 ダイクストラのアルゴリズムでは、 優先度キューを使用して漸近時間を変更できます。
状態の置換
決定において、ダイナミクスには常に状態が含まれます。これは、サブタスクを一意に指定するパラメーターですが、必ずしもこの状態が唯一の状態ではありません。場合によっては、他のパラメータを思いついて、漸近的な時間または記憶の減少という形でこの恩恵を受けることができます。
例9：数値の分解
数
N
をさまざまな用語に分解する数を見つける必要があります。たとえば、の場合
N = 7
、そのような展開
5
：
- 7
- 3 + 4
- 2 + 5
- 1 + 7
- 1 + 2 + 4
状態の異なる2つのソリューション
1) :
—
,
.
, , .
2) :
,
.
3) :
4) : ,
.
5) —
.
:
, : 
。 漸近： 
。
1) . dp[n][k] —
. , .
2) :
,
.
3) :
, . ( ) :
, :
.
, — . — , , — : .
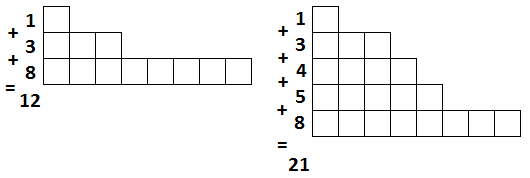
4) : ,
.
, , 
. , —
,
(
). ,
。
5) —
.
漸近： 。
№1:
1) :
dp[n][k]
—
n
,
k
.
k
, , .
2) :
dp[1][1] = 1
,
dp[1][i] = 0
.
3) :
for last_summand in range(1, k + 1): dp[n][k] += dp[n - last_summand][last_summand]
4) : ,
n
.
5) —
dp[N][1..N]
.
:
。 漸近： 。
№2:
1) . dp[n][k] —
n
k
. , .
2) :
dp[1][1] = 1
,
dp[1][i] = 0
.
3) :
dp[n][k] = dp[n - k][k] + dp[n - k][k - 1]
, . ( ) :
-
1
. -
1
.1
.
, :
.
, — . — , , — : .
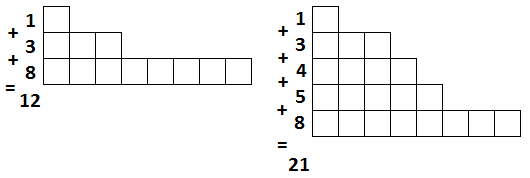
4) : ,
n
.
,
. , — k
N
,
( 1
k
). ,
5) —
dp[N][1..k_max]
.
漸近：
おわりに
主な情報源は校長で、情報はサマーコンピュータースクール（児童向け）での講義、アンドレイスタンケビッチのサークル、ミハイルドヴォルキン（darnley）の特別コースから得られました。
ご清聴ありがとうございました。この記事が誰かに役立つことを願っています！私は便利になりましたが、記事を書くことはすべてを覚える良い方法であることがわかりました。