👧🏽 👨🏼‍🎤 🧑🏼 流体力学シミュレーション：格子ボルツマン法 💅🏾 🚣🏼 ⛺️

火山噴火のシミュレーション

格子ボルツマン法を使用。（c）ソース

この記事では、 Lattice Boltzmann Method （LBM）の流体力学をモデル化するための数値的手法について説明します。ロシア語では、格子ボルツマン方程式の方法。並列化の容易さ、多相流をシミュレートする機能、および多孔質媒体内の流れをシミュレートする能力において、他の既知の方法（たとえば、有限要素法）をしのぐさらに、計算アルゴリズムには最も単純な算術演算のみが含まれています。この方法は非常に新しく、それに基づいた最初の商用製品が2010年頃に登場し始めました。

ハブには流体物理学に関する一連の記事が既にありましたが、この記事はその論理的な続編かもしれません。これは、流体力学とモデリング方法をよく知っている人々に役立つように書かれており、この分野の初心者（たとえば、ソフトウェアエンジニアの教育を受けた人々）に理解できるものです。もちろん、この点に関しては、専門家にとって詳細すぎるものが多くあり、十分なスペースがないものもあります。記事はかなり大きいことが判明しましたが、いくつかの部分に分けたいとは思いません。

なぜこれがすべて必要なのですか？より正確には、どの産業で流体力学をシミュレートする必要があるか：

航空機建設、ロケット科学、自動車産業（車体特性、エンジン運転、ノズル）
工業化学（物質の分離、化学反応器）
気象学、地質学（多孔質媒体、砂岩、ダムを通る流体の流れ）
その他のエンジニアリング産業（風力発電所）
薬（血流、リンパ）

この記事には次のセクションが含まれます。

物理学のレビュー-基本的な必須方程式の高レベルのレビュー
基本的な考え方は、アルゴリズムの基本原理の説明です
技術的詳細—ソース方程式のより詳細な説明、計算スキーム
- ナビエ・ストークス方程式
- ボルツマン方程式
- 離散ボルツマン方程式
- コンピューティング図
- 空間回折格子
- 平衡分布関数
- 非圧縮性
- 粘度とレイノルズ数
- もう一度、すべて一緒に
雑多
- アルゴリズムの追加
- 落とし穴
- 既存のソリューション
- 何を読む

物理の概要

流体力学と空気力学は、ナビエ・ストークス方程式によって巨視的に記述されます。初期および境界条件と媒体のパラメーターに応じて、各瞬間における空間の各点での液体の圧力、密度、速度がどのようになるかを示しています。

一方、希薄気体の場合、空間の各点での粒子速度分布密度が時間とともにどのように変化するかを説明するボルツマン方程式が有効です。特定のポイントで粒子速度分布を統合すると、特定のポイントで密度と巨視的速度を取得できます。言い換えれば、巨視的には、ボルツマン方程式はナビエ・ストークス方程式と同等です。

主なアイデア

密度の高い液体の場合、ボルツマン方程式は適用できないという事実にもかかわらず、それをモデル化することを学べば、これらの液体のナビエ・ストークス方程式もモデル化できます。つまり、それによって抽象化の基礎レベル（高密度液体の微視的方程式）を物理的に正しくない実装（希薄気体の微視的方程式）に置き換えますが、上位レベル（巨視的ナビエ・ストークス方程式）は正しく記述されます。

この状況を下の図に示します。

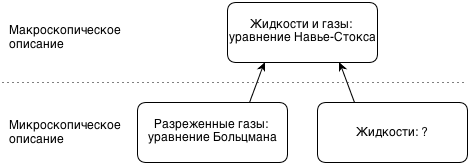
格子ボールツマン法のアイデア

その中の疑問符は、どの方程式が微視的レベルでの高密度液体の挙動を説明するのかわからないという事実を象徴しています。時々、彼らは「微視的」の代わりに「メソスコピック」と言います-微視的記述は個々の原子と分子の挙動の記述であり、ボルツマン方程式は分子の流れを記述するという意味で。

コンピューターは連続量の操作方法を知らないため、ボルツマン方程式を離散化する必要があります：時間、空間座標（モデリング用の空間ノードを取得）、および各空間ノードで可能な粒子方向。方向は特別な方法で選択され、常にいくつかの隣接ノードを指します。

技術的な詳細

この大きなセクションには、元の方程式のより詳細な説明と計算スキームの導出が含まれています。本当に重要な方程式は、技術的背景を持つすべての読者にとって明確でなければなりません（線形代数の基礎、積分計算が必要です）。理解できないそれらの方程式は、おそらく重要ではありません（これらはnablaがある場合です）。ベクトルは太字で示されています。

ナビエ・ストークス方程式

非圧縮性の液体と気体の巨視的な動力学の方程式の変形は次のようになります。

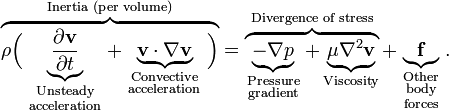ナビエ・ストクス方程式

（1）

ここで、vは流速、ρは流体の密度、pは流体内の圧力、fは外力（重力など）です。

逆三角形と偏導関数が何であるかわからなくても心配する必要はありません。将来必要になることはなく、計算アルゴリズムには最も単純な算術演算のみが含まれます。

詳細な結論と物理的な意味はWikipediaとHabréで調べることができますが、ここでは主なアイデアを示します。

液体中の少量を精神的に選択し、その動きを追跡します。所定量の流体に作用する加速度は、（i）左、右、上、下などの圧力によって決まります。（さらに、それらは互いに部分的に補償します）、（ii）流体内の内部摩擦力の作用によって（iii）外力によって。一方、加速度は、初期時点の初期時間と、液体の体積が存在する新しい時点の次の時点の速度の差で表すことができます。

これらの量をニュートン方程式F = maに代入すると、単純な変換の後、上記の方程式が得られます。左側はma、右側はFです。

ボルツマン方程式

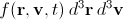この方程式は、座標と速度f（r、v、t）に沿った粒子の確率密度の分布関数で動作します。値f（x、y、z、v _x 、v _y 、v _z 、t）dx dy dz dv _x dv _y dv _zは、時間tでの粒子の割合がxからx + dx、yの立方体にあることを示しますto y + dy、zからz + dz、速度はv _xからv _x + dv _x 、v _yからv _y + dv _y 、v _zからv _z + dv _z 次のように書くこともできます f（r、v、t）d ^ 3r d ^ 3v

。

この関数は通常、調査中のシステム内のガスの質量に正規化されているため、各ポイントでの巨視的なガス密度は、すべての可能な速度値について、特定のポイントでの確率密度の合計（積分）として決定されます。

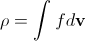。（2）

同様に、巨視的な速度は

。（3）

方程式を導出するための基本的な考え方は、ナビエ・ストークス方程式の導出に似ています。与えられた小さな体積内の与えられた瞬間に、与えられた方向（より正確には狭い方向の円錐）に飛ぶ分子のビームを精神的に隔離しましょう。 dtの短い時間の後、それらは（速度の存在により）隣接点にあり、外力による分子の加速により速度自体が変化します。さらに、パスのこのセグメントでは、一部の分子が他の分子と衝突して速度が変化し、元のビームに含めることができなくなります。一方、反対方向に飛んでいる同じ体積の分子の衝突の結果として、それらのいくつかは速度の望ましい方向を獲得し、それらをビームに追加します。

これは次のように記述できます。

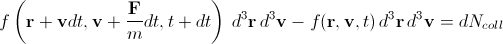$ボルツマン導出、f \左（\ mathbf {r} + \ mathbf {v} dt、\ mathbf {v} + \ frac {\ mathbf {F}} {m} dt、t + dt \ right）\、d ^ 3 \ mathbf {r} \、d ^ 3 \ mathbf {v} -f（\ mathbf {r}、\ mathbf {v}、t）\、d ^ 3 \ mathbf {r} \、d ^ 3 \ mathbf {v} = dN_ {coll}$ 、（4）

ここで、Fは外力、mは分子の質量、dN _collは衝突によるビーム内の粒子数の変化です。

一般的な用語で決定されるように、dN _collの値はリーダーから隠されたままになります。必要なのは、その標準的な近似であるBatnagar-Gross-Crook （BGK）だけです。この近似では、dN _collは次と等しくなります。

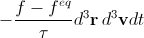$BGK近似、-\ frac {ff ^ {eq}} {\ tau} d ^ 3 \ mathbf {r} \、d ^ 3 \ mathbf {v} dt$ 、（5）

ここで、f ^eqは平衡分布関数、 Maxwell-Boltzmann分布、τはいわゆる緩和時間です。

結果として、

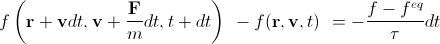$ボルツマン導出、f \左（\ mathbf {r} + \ mathbf {v} dt、\ mathbf {v} + \ frac {\ mathbf {F}} {m} dt、t + dt \右）\-f（ \ mathbf {r}、\ mathbf {v}、t）\ =-\ frac {ff ^ {eq}} {\ tau} dt$ 。（6）

f ^eqは、特定のポイントでの巨視的な密度と速度に依存することに注意してください（つまり、暗黙的に座標と時間に依存します）。将来必要になるのはこの方程式ですが、通常はdtで除算され、

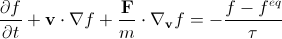$ボルツマン方程式、\ frac {\ partial f} {\ partial t} + \ mathbf {v} \ cdot \ nabla f + \ frac {\ mathbf {F}} {m} \ cdot \ nabla _ {\ mathbf {v} } f =-\ frac {f- f ^ {eq}} {\ tau}$ 、（7）

ここで、インデックスvのnablaは、速度変数に関してnablaです。

離散ボルツマン方程式

コンピューターで連続ボルツマン方程式のダイナミクスをシミュレートできるようにするには、離散化する必要があります。これを行うには、まず空間座標の均一なグリッドを導入します。グリッドのステップをすべての軸に沿って同じにします。液体の挙動は、グリッドのノードで正確に決定されます。実際、特定の空間ノードにのみ分子を配置できます。さらに、時間を離散化する必要があります。液体の状態を互いに等しい時間で判断します。さらに、分子が特定の速度値のみを持つことを許可します。これにより、時間ステップで分子が隣接ノードに移動できるようになります。これらの許可された方向は、すべての空間ノードで同じです。明らかに、対角線方向の粒子速度は、非対角線方向の粒子速度よりも大きくなります。

直感的には、無限に小さな時間ステップと空間格子ステップで、この離散システムは通常のボルツマン方程式に進み、巨視的限界のナビエ・ストークス方程式に進むと結論付けることができます。奇妙なことに、これはそれほど単純な質問ではなく、今のところ延期します。

さらなる説明では、格子のステップが長さの単位であり、時間のステップが時間の単位であるような単位系であると想定されています。

簡単にするために、以下では外力がないと仮定します。インデックスiを使用して、許可された速度方向に1からQまでの番号を付けます。ここで、時間ステップで特定のノードから方向iに飛行する粒子の質量をf _iで表すと、式（6）は次のようになります。

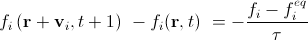$離散ボルツマン、f_i \左（\ mathbf {r} + \ mathbf {v} _i、t + 1 \右）\-f_i（\ mathbf {r}、t）\ =-\ frac {f_i-f_i ^ {eq }} {\ tau}$ 。（8）

ここでは、タイムステップが1に等しいことを考慮し、（6）のすべてのdtを1に置き換えました。 f _i ^eqは、特定のノードでの巨視的な質量と速度に依存する離散的な平衡分布密度を示します。どの特定のノードからf _i ^eqを使用するかは示しませんでした。時間t + 1ではr + v _i tから、時間tではrからです。計算スキームでは、時刻t + 1でノードr + v _i tを使用する方が便利であることがわかります。その後、上記の方程式は、拡散ステップと衝突ステップの2つのコンポーネントに分解できます。

ストリーミングステップ：

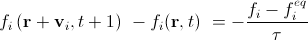$ストリーミング、\ tilde {f} _i \ left（\ mathbf {r} + \ mathbf {v} _i、t + 1 \ right）\ = f_i（\ mathbf {r}、t）\、$ 。（9）

衝突ステップ：

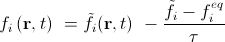$衝突、f_i \左（\ mathbf {r}、t \右）\ = \チルダ{f} _i（\ mathbf {r}、t）\-\ frac {\チルダ{f} _i-f_i ^ {eq} } {\ tau}$ 。（10）

ここで、チルダ付きのf _iは、i方向のサイトに到着したが、到着した他の粒子とまだ衝突していない粒子の質量を示します。ストリーミングステップは、移流ステップと呼ばれることもあります。

離散化された速度方向の場合、各ノードの質量と巨視的速度は次のように計算されます。

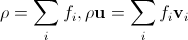$密度と速度の離散、\ rho = \ sum_ {i} f_i、\ rho \ mathbf u = \ sum_ {i} f_i \ mathbf v_i$ 。（11）

以下では、格子の単一の空間ステップで、単一のボリュームが各ノードに関連付けられ、質量と密度の値が一致するため、質量ではなく密度をどこにでも記述します。

平衡分布関数は、節点の質量と巨視的な速度に依存することを示します。したがって、ストリーミングステップの後、各ノードの質量と速度を再計算し、平衡分布関数を再計算してから、衝突を起こす必要があります。

したがって、計算スキームの各ステップで、粒子を「伝播」する必要があります。つまり、ノードrから方向iに飛ぶ粒子をノードr + v _iに移動する必要があります（すべての粒子と方向でこれを行います）。この後、質量、速度、および平衡分布関数を再計算する必要があります。最後に、特定のサイトに到着した粒子を「衝突」させる必要があります。つまり、粒子を方向に再分配します。

コンピューティング図

2次元システムの例で計算スキームを説明します。空間ノードへの離散化とそれらの間の関係（つまり、許容される速度の方向）を以下の図に示します。空間ノードは円で示され、ノード間の接続は細い線で示されます。

D2Q9

次の図は、ストリーミングと衝突のペアの1つの反復を示しています。色付きの矢印は、飛ぶ分子の流れを表しています。色の強さは、特定のストリームを飛行する分子の質量をエンコードします。矢印の長さは、タイムステップでストリームが移動する経路にほぼ対応します（矢印はノードの中心からノードの中心に移動する必要があるため、およそのみです）。

衝突移流

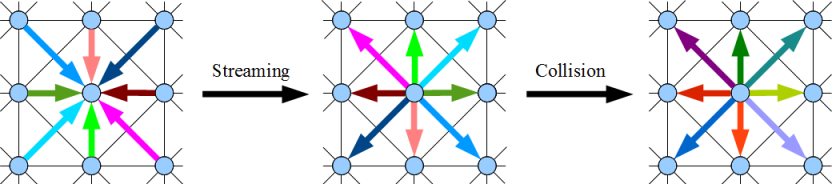
空間回折格子

LBMでは、ラティスは許容される速度ベクトルのセットです（各空間ノードで同じ）。これは、エンティティとしてのラティスの標準的な数学的な定義と一貫性があり、並列転送によって空間グリッド全体を取得できます。

LBMでは、ラティスにはノードからそれ自体へのゼロベクトルが含まれている必要があります。これは、特定のノードからどこにも飛ばないパーティクルを表します。 LBMでは、ラティスは通常、略語DnQmで示されます。ここで、nは空間の次元、mはラティスのベクトルの数です。たとえば、D2Q9、D3Q19など。

2次元LBM空間では、ラティスは、たとえば、5つのベクトル（ノードからそれ自体への2つの垂直、2つの水平ベクトルおよびゼロベクトル）で構成するか、上の図のように9つのベクトル（垂直2、水平2、対角4、1ゼロ）。これらは、それぞれD2Q5およびD2Q9ラティスです。

ラティスを選択するための明らかな要因は次のとおりです。1.シミュレーションの精度（直感的に、ラティス内のベクトルが多いほど、シミュレーションの精度が上がります）2.計算コスト（D2Q5ラティスでの計算はD2Q9での計算よりも速くなります）。奇妙なことに、これらは最も重要な要因ではありません。最も重要な要因は、Navier-Stokes方程式の再現性と、格子ベクトルに基づくいくつかのテンソルの対称性です。

一般的に使用されるグリルは、D2Q9、D3Q15、D3Q19です。グリルD2Q9およびD3Q19を以下に示します。基本的な格子ベクトルは、通常e _iまたはc _i （単位時間ステップで以前に導入された速度v _iと一致します）として示されます。以下では、表記e _iを使用します。

D2Q9

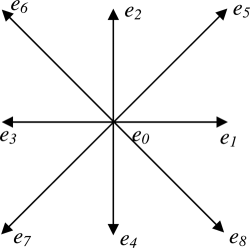
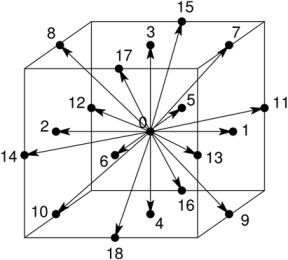
D2Q9の基底ベクトルを記述します。

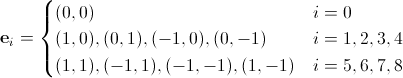$D2Q9ベクトル\太字{e} _i = \ begin {cases}（0,0）＆i = 0 \\（1,0）、（0,1）、（-1,0）、（0、-1）＆i = 1,2,3,4 \\（1,1）、（-1,1）、（-1、-1）、（1、-1）＆i = 5,6,7,8 \ \ \ end {cases}$ （11）

およびD3Q19の場合：

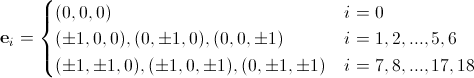$D3Q19ベクトル\太字{e} _i = \ begin {cases}（0,0,0）＆i = 0 \\（\ pm 1,0,0）、（0、\ pm 1,0）、（0、 0、\ pm 1）＆i = 1,2、...、5,6 \\（\ pm 1、\ pm 1,0）、（\ pm 1,0、\ pm 1）、（0、\ pm 1、\ pm 1）＆i = 7.8、...、17.18 \\ \ end {cases}$ （12）

繰り返しますが、タイムステップはユニティに等しいと仮定しているため、v _i = e _iです。

平衡分布関数

連続的な場合、平衡分布関数（ Maxwell-Boltzmann分布）は

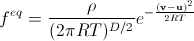$Maxwell分布、f ^ {eq} = \ frac {\ rho} {（2 \ pi RT）^ {D / 2}} e ^ {-\ frac {（\ bold {v}-\ bold {u}）^ 2} {2RT}}$ 。（13）

以前は未知の量があります：Rは普遍的な気体定数、Tは温度、Dは空間の次元、vは速度ベクトルで、確率密度を求めます。ここでは、ガスのモル質量は1に等しくなります（私たちにとっては重要ではありません-巨視的な密度のみが重要です）。これは、シミュレーションでの質量単位の変化と考えることができます。さらに、関数は局所的な巨視的な密度に正規化され、統一性ではありません。また、通常、ガスuの巨視的な速度はvから取り除かれないことに注意してください。これは通常、定常ガスの場合に分布が研究されるためですが、Maxwell-Boltzmann分布を使用するには、特定の時点で特定の点で現在のガス速度で移動する局所慣性基準座標系に移動する必要があります。 uを引くと、そのような遷移になります。

空間内の特定のポイントで、分子の速度分布が平衡になったと仮定します。この分布は、巨視的な質量ρと速度uに依存します。一方、分布関数からρとuを計算できます（式（2）および（3）を参照）。明らかに、この計算は正しいρとuを与える必要があります（つまり、ある意味では、これは分布関数に対する追加の制限です）。

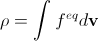$密度平衡、\ rho = \ int f ^ {eq} d \ mathbf v$ 、 $速度平衡、\ rho \ mathbf u = \ int f ^ {eq} \ mathbf v d \ mathbf v$ 。（14）

離散的な場合の密度と速度の計算に同じ要件を課します。

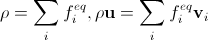$密度と速度の離散平衡、\ rho = \ sum_ {i} f ^ {eq} _i、\ rho \ mathbf u = \ sum_ {i} f ^ {eq} _i \ mathbf v_i$ 。（15）

離散平衡分布関数の主な要件は、無限小時間ステップと格子ステップの極限でのナビエ・ストークス方程式の再現です。これは、与えられたρとuについて、連続ケースと離散ケースで平衡分布関数を使用してそれらを再度計算しようとすると、結果が一致するという事実に相当します（離散ケースでは質量は密度ではなく質量を意味するという上記の注意を参照）。 e。

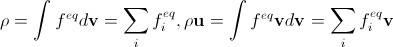$密度と速度の等式、\ rho = \ int f ^ {eq} d \ mathbf v = \ sum_ {i} f ^ {eq} _i、\ rho \ mathbf u = \ int f ^ {eq} \ mathbf vd \ mathbf v = \ sum_ {i} f ^ {eq} _i \ mathbf v$ 。（16）

平衡離散分布関数を一意に決定するには、特定のポイントでの巨視的な熱エネルギーの等価性に関する同様の要件も含める必要がありますが、簡潔にするために省略しています。

速度の方向に沿った衝突ステップの式（10）を要約すると、式（16）を考慮に入れると、衝突ステップがサイト内の分子の巨視的な質量と速度を変えないことを示すことができます。

（11）と（12）からの離散速度ベクトルe _i = v _iを単純に連続平衡分布関数（13）に代入すると、等式（16）は成り立たないことがわかります。

また、Maxwell-Boltzmann分布（13）をTaylor級数で巨視的速度の2次まで拡張すると、等式（16）を保持できることがわかります。これは、u / sqrt（RT）が非常に小さいという事実に対応しています。この制限は、すべてのノードでのシミュレーションプロセス中に常に満たされる必要があります。

しかし、テイラー級数に拡大しても十分ではありません。また、離散関数f _i ^eqに特別に選択された因子w _iを導入する必要があります（計算の詳細はこの美しい記事にあります- 無料版もあります;もちろん、すべては表面的な説明よりも少し複雑になります-実際、計算は起こります）格子ベクトルに基づいて、最大4ランクまでのテンソルを介して）。最後に取得

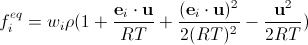$Maxwell分布離散、f ^ {eq} _i = w_i \ rho（1+ \ frac {\ vec {v_i} \ cdot \ vec {u}} {RT} + \ frac {（\ vec {v_i} \ cdot \ vec {u}）^ 2} {2（RT）^ 2}-\ frac {\ vec {u} ^ 2} {2RT}）$ 。（17）

キャッチがあります：格子のピッチと時間はそれぞれ長さと時間の単位であると常に仮定します。したがって、SIからRの値を取得することはできず、ここでの温度はケルビンでシミュレートされた流体の温度と等しくありません。

それらの値を決定するために、次のことに注意してください。流体に乱れがあると仮定します。つまり、いくつかのノードに過剰な質量があります。この質量は、空間、さらに摂動領域の右端のノードで「広がり」始め、3Dの方向（1、0、0）または2Dの（1、0）に移動します。時間の単位では、これらの方向に沿った分子は長さの単位を通過します。つまり、速度は1に等しくなります。これは、システム内の外乱の伝播速度としての音速も1に等しいことを意味します。一方、音速はsqrt（γRT /μ）に等しく、ここでγは断熱定数、μはモル質量であり、これは以前に1に等しいと仮定しました。断熱定数γは1 + 2 / dです。dは分子の自由度の数です。理想的な気体では、それは空間の次元に等しい。私たちのガスでは、分子はノードを結ぶ直線に沿ってしか移動できないため、次元は3（または2）ではなく1です。つまり、γ= 3、sqrt（3 RT）= 1です。

通常、LBMの文献では、「音速」とは

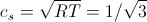$音速、c_s = \ sqrt {RT} = 1 / \ sqrt {3}$ 。（18）

さて、ついに、

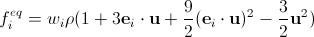$Maxwell分布離散、f ^ {eq} _i = w_i \ rho（1 + 3 \ mathbf {e} _i \ cdot \ mathbf {u} + \ frac {9} {2}（\ mathbf {e} _i \ cdot \ mathbf {u}）^ 2- \ frac {3} {2} \ mathbf {u} ^ 2）$ 。（19）

最も一般的な格子の係数w _iの値を書きます。

D2Q9の場合：

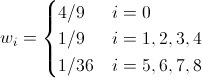$D2Q9の重みw_i = \ begin {cases} 4/9＆i = 0 \\ 1/9＆i = 1,2,3,4 \\ 1/36＆i = 5,6,7,8 \\ \ end {ケース}$ （20）

D3Q19の場合：

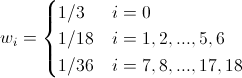$D3Q19の重みw_i = \ begin {cases} 1/3＆i = 0 \\ 1/18＆i = 1,2、...、5,6 \\ 1/36＆i = 7,8、... 、17、18 \\ \ end {cases}$ （21）

非圧縮性

小さな巨視的な流体速度の制限は、次のように記述できます。

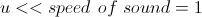$非圧縮性、u << speed of \ sound = 1$ 。（22）

マッハ数は、システム内の特徴的なガス速度と音速の比であることを思い出してください。次に、上記の制限は小さなマッハ数または非圧縮性流体に対応します。実際、音速（密度摂動の伝播速度）が大きい場合、密度摂動はシステム全体に急速に広がり、密度は再び同じになります。つまり、1つのローカルエリアで液体を圧縮することに成功しません。

ノードでの巨視的速度の適切な最大値は、たとえば0.01です。

粘度とレイノルズ数

LBM の動粘度 ν（通常、格子単位）は、次のように計算されます。

$粘度、\ nu =（\ tau-1/2）c ^ 2_s =（\ tau-1/2）/ 3$ 。（23）

ここで、τは式（5）で前述した緩和時間であり、 _s = 1 / sqrt（3）は（18）で導入した「音速」です。

温度変化を考慮せずに流体力学をモデル化する場合、所定のジオメトリを持つシステム（たとえば、断面が正方形のパイプ）は、1つの無次元パラメーター（レイノルズ数）で完全に記述されます。

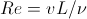$レイノルズ、Re = v L / \ nu$ 、（24）

ここで、vはシステムの特性速度（たとえば、パイプの中心の速度）、Lはシステムの特性長（たとえば、正方形断面の辺の長さ）です。

標準形状の場合、通常、特性速度と外力（流れを提供する）の関係は既知です。したがって、特定のレイノルズ数でモデリングするには、次が必要です。

特性速度vを選択します。わかったように、音の速度よりもはるかに小さいはずです。たとえば、0.01。
そのような速度に必要な外力を計算する
（23）に従って粘度を計算し、目的のレイノルズ数を取得する
（24）から緩和時間を計算して、目的の粘度を得る

シミュレーション問題がSI単位でコンパイルされている場合（仮に、正方形のパイプ断面の側面が1 m、パイプ入口の圧力がXパスカル、出口で— Yパスカル）、最初に無次元のレイノルズ数を見つけ、上記のアルゴリズムを使用する必要があります。

もう一度、すべて一緒に

モデリングの前に、各ノードで初期の巨視的な質量と速度を設定する必要があります。次に、各ノードで許可された各方向e _iの質量流量を設定します（落とし穴を参照）。最も簡単な方法は、平衡分布からのフローを示すことです。

ループコミットでシミュレートするには

式（9）によるストリーミングステップ
式（11）による各ノードの巨視的な質量と速度の再計算、式（19）によるすべての方向の平衡流の再計算
式（10）による衝突ステップ

モデリングは通常、システムが静止するまで行われます。定常性は、たとえば、隣接するステップ間の各ノードの巨視的な速度と質量の差、すべてのノードの最大値によって確認できます。

雑多

アルゴリズムの追加

モデリングに外力を含めること（たとえば、重力）には触れませんでした。これらは、ストリーミングステップの式（9）に少し追加されます。

境界条件にも触れませんでした-ボディの表面、システムの入口と出口（たとえば、パイプの入口に一定の圧力または速度フィールドが指定されている場合）。メソッドは微視的レベル（分子の流れ）で定式化され、そのような境界条件は巨視的レベルで定式化されるため、LBMはそのような条件のモデリングに大きな自由があります。顕微鏡レベルで境界条件を設定するには多くの方法があり、多くのアルゴリズムがあります。

no-slip boundary conditions ( ). bounce-back conditions ( ). , 4.6.

, , single relaxation time. , , multiple relaxation time ( , double relaxation time).

LBM ( ).

LBMでは、熱伝導率の存在（つまり、システム内の熱伝達、システム内のさまざまなポイントでの温度の変化、およびその結果、システムパラメーターの変化（密度など））もサポートされます。温度は、同じくLBMアルゴリズムを使用して、別個の「気体」としてモデル化されますが、この気体の速度は主流体の速度によって決まります。この意味での温度は受動的なスカラーであると言われています。LBMを介したレイリー-ベナール対流現象のモデル化に関する多くの記事があります。効果的な実装と並列化の問題にはまったく触れませんでした。

落とし穴

熱伝導率を使用してシステムをモデル化する場合、2つの無次元量で記述されます。レイリーベナール対流の場合、プラントル数とレイリー数が通常選択されます。このシステムを格子単位で再現するためには、システムの内部パラメーター（特性速度、外力、熱伝導率）を正しく設定することにより、これらの無次元量の両方を再現するだけでは十分ではありません。実際には、内部パラメーター間に非表示の依存関係が存在します。詳細はこちらをご覧ください。

すでに述べたように、システムで特徴的な速度を選択するとき、マッハ数が1よりもはるかに小さいことを忘れないでください（式（22））。

LBMは、レイノルズ数が大きいシステムでは不安定になる可能性があります（ただし、流れがまだ層流の場合）。

LBM では、ガリレオ不変性は成り立ちません。ただし、これは通常重要ではありません。

シミュレーションの開始時に、許可されたすべての方向の各ノードからの分子の流れを指定する必要があります。流れの平衡分布がしばしば選択されます（式（19））。平衡は定常性を意味しないことを覚えておくことが重要です。つまり、速度、外力などの勾配がある場合の定常分布です。平衡とは異なります。それらの計算をここに示します（参照により式12、19、20）。

既存のソリューション

LBM専用の大規模で非常に成熟したオープンソースプロジェクト、Palabos（PArallel LAttice BOLtzmann）があります。プロジェクトにはwikiもあります。開発者は、流体力学のモデリングに関する有料のアドバイスを提供します。MATLABでの典型的なシステムのモデリングに関する優れたチュートリアル例

があります。たとえば、レイリー–ベナール対流（外力、熱伝導率、境界条件、量の正しい変換がある場合）。MATLABでは合計160行。

たとえば、thisまたはthatなど、多くの商用ソリューションがあります。

商用および非商用のLBMパッケージの詳細なリストは、Wikipediaにあります。

何を読む

記事にあるすべてのリンクに加えて、これらの記事と書籍のリストを推奨できます。基本的に、同様の書籍のリストがWikipediaにあります。

それだけです

流体力学シミュレーション：格子ボルツマン法