3、7、11、および4で割ったときに3の剰余を与える他の数値がa 2 + b 2の形式で表現できない理由を理解するのは非常に簡単です:偶数の2乗は常に4で除算し、奇数の2乗は常に4で割ったとき剰余1を与えます、4で割ったときの2つの平方の合計は、0、1または2の剰余を与えることができますが、3ではありません。4k+ 1の形式の素数の表現可能性は明白ではありません(特に、単純さが不可欠であることに気づいた場合:望ましい21の数21は、合計が2です正方形なし)。
控除
自然数は無限にあります。 いくつかの理由でそれらをクラスに結合すると便利です。 特に、ある数nによる除算の剰余を結合すると、 nを法とする剰余になります。剰余x̅は、 nで除算するとxと同じ剰余を与えるすべての数のクラスです。 これは同等であり、剰余x̅はx + n∙kの形式のすべての数で構成されます。ここで、 kは整数です。 この投稿のフレームワーク内では、すべての残基はモジュロp (導入部と同じ奇数の素数)になります。 当然、 pで除算した残基、つまり正確にpの残基と同じ数の異なる残基があります。 自然数の無限と比較して、残基への移行はオプションの数を大幅に減らします。
クラス操作は常に意味をなさない。 たとえば、素数のクラスを複合数のクラスに追加しようとしても意味がありません。数字のみを追加でき、素数と複合数の合計にはクラスに共通のプロパティが表示されません。 トートロジークラブのメンバーは、素数のクラスと複合数のクラスを合計すると、素数と複合数の合計で合計できる数のクラスを与えると言うことができます。
ただし、控除の場合、自然数から「継承」される加算、減算、および乗算は、他の控除を与えます。 たとえば、2̅+3̅=5̅:剰余2の任意の数を取り、残り3の任意の数を取り、それらの合計は間違いなく5の剰余を与えます。不快なモジュール6。 しかし、単純なモジュールの場合、明らかに、これは起こりません。彼らが言うように、 ゼロ除数はありません 。 さらに、 a̅=0̅の場合を除き、任意の2つの剰余について方程式a̅∙x̅=b̅ (除算)を解くことができ、結果は一意に決定されます。 一意性は、非ゼロの剰余の積が非ゼロであるという事実から得られます。 a̅≠0̅であるため、 aとpの最大公約数は1です(ここでも単純さpが必要です)。 拡張ユークリッドアルゴリズムは、 a∙x + p∙y = 1のようにxとyを見つけます。つまり、 a̅∙(b̅∙x̅)=b̅となります。
ゼロ除数がないことの重要な結果:次数nの単一変数の非ゼロ多項式は、 nを超える根を持つことはできません。 (これは通常の整数ではよく知られていますが、剰余演算を使用する場合、追加の正当化が必要です。3̅∙x̅=0̅6を法とする3つの解0̅、2̅、4̅があります。)実際、通常の「列」除算は多項式f(x)は、 f(x)=(x-c)g(x)+ (定数)として表すことができます。ここで、多項式g(x)の次数は1未満です。 cがf(x)の根である場合、定数はゼロ( x = cを代入)です。 c 'がf(x)の別のルートである場合、 g(x)のルートになります(ここではゼロ除数がないことが重要です)。したがって、プロセスを続行できます。 n個の根が既に蓄積されている場合、残りのg(x)は定数であり、さらにゼロ以外(f(x)= 0 )であり、根はもうありません。
単純なモジュールによる控除は、加算、減算、乗算できます。 非ゼロの控除は分割できます。 これらすべての操作には、タイプa̅∙b̅=b̅∙a̅の通常のプロパティがあります。 スマートブックは、単純なモジュールによる控除がフィールドを形成すると言います (そして、分割することが不可能で、他のすべてが同じである複合モジュールによる控除は可換環です )。 そして、この分野を有限と呼ぶのに賢い本である必要はありません。 残差フィールドは唯一の有限フィールドではありませんが、他の最終フィールドは必要ありません。
楕円曲線について少し
pを法とする楕円曲線(同じ奇数素数)は、方程式y 2 = x 3 + a 2 x 2 + a 4 x + a 6の解の集合と考えることができます。ここで、 x 、 y 、およびすべてのaは剰余です(各解は1と呼ばれます) point )に加えて、ペアx、yを持たない1つの特別なポイントO。 方程式の右辺は正方形で除算しないでください。そうしないと楕円曲線になりません。タイプy 2 =(x-1̅) 2 (x +2̅)の方程式では、変数yをz = y /(x-1̅)に置き換えて依存関係を取得できます3度ではなく2度。
p≠3の場合、変数xの代わりにx + a 2/3を取り 、 x 2の項を取り除きます。
x、yは有限集合に属するため、楕円曲線上の点の数も有限であることは明らかです。 それらのいくつ? これは一般的に難しい質問です。 y 2 = x 3 -k∙xの形式の曲線に制限します。 そのような曲線の場合、完全な証明を1つのHabrポストに入れることができます(かなり長いものですが)。
二次控除と非控除
まず簡単な質問をしてみましょう。 方程式y 2 = cの解はいくつありますか。ここで、 y、cは剰余です。 p = 7の例:
| y | 0̅ | 1̅ | 2̅ | 3̅ | 4̅ | 5̅ | 6̅ |
| y 2 | 0̅ | 1̅ | 4̅ | 2̅ | 2̅ | 4̅ | 1̅ |
解が存在するcの非ゼロの剰余は、 2次剰余と呼ばれます。 解が存在しない剰余cは2次剰余と呼ばれます。 二次的な非控除は控除であることに注意する価値があります。二次的であることは彼が幸運ではなかったというだけです。 ルジャンドル記号
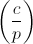 cと2乗の関係を示します。適用される場合は1(つまり、 cは二次剰余)、-1が適用されない場合(つまりcは二次剰余)、 c =0̅の場合は0です。 方程式y 2 = cの解の数は
cと2乗の関係を示します。適用される場合は1(つまり、 cは二次剰余)、-1が適用されない場合(つまりcは二次剰余)、 c =0̅の場合は0です。 方程式y 2 = cの解の数は 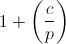 。
。
楕円曲線に戻ります。 固定xのオプションyの数、曲線上のポイントの総数y 2 = x 3 -k∙xは、すべてのxを合計し、特別なポイントを忘れずに書き留めることができます。
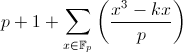 。 前に現れなかったシンボルF pによって、 pを法とする剰余のフィールド(フィールド)を示すのが慣例です。
。 前に現れなかったシンボルF pによって、 pを法とする剰余のフィールド(フィールド)を示すのが慣例です。
これで、2乗和のpの展開の成分の約束された式を提示する準備ができました。 定理 gを任意の2次非剰余とします。 pを4で除算して余り1が得られる場合、
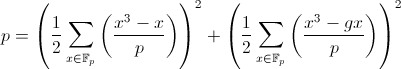
また、最初の括弧内の数字は奇数の整数であり、2番目の括弧内の数字は偶数の整数です。 pを4で除算すると、剰余が3になる場合、括弧内の両方の合計はゼロになります(つまり、楕円曲線上の点の数はp + 1になります )。
証明
ポストはすでに長いため、証拠はネタバレの下で削除されます。 知覚を損なうことなく安全にスキップできます。
パート1。ケースp = 4k + 3およびパリティ/奇数の問題。
非ゼロの残基cを取得し、それを1̅からp̅- 1allまでのすべての残基で乗算すると、すべての積は非ゼロであり、ペアごとに異なります( c∙x = c∙yの場合、 c∙(xy)= 0 which x = yの場合のみ)、つまり、 1̅からp̅-1̅までのすべての残基のある種の順列になります。 したがって、 1̅∙2̅∙...∙(p̅-1̅)=(c∙1̅)∙(c∙2̅)∙...∙(c∙(p̅-1̅))= c p-1 ∙1̅∙2̅ ∙...∙(p̅-1̅)およびc p-1 =1̅(ゼロ以外の剰余cの場合) (これはフェルマーの小さな定理の証明でした 。)
したがって、多項式x p-1 -1 =(x (p-1)/ 2 -1)(x (p-1)/ 2 +1)の根はp-1です。 したがって、各ブラケットには(p-1)/ 2のルート(ブラケットの次数の最大可能数)があります。 各二次剰余は、最初のブラケットのルートです( x = c 2の場合、次にx (p-1)/ 2 = c p-1 =1̅ )、それらの(p-1)/ 2があります 。つまり、すべての二次剰余に対して2番目のブラケットが残ります。 したがって、 cのルジャンドル記号はc (p-1)/ 2と同じ残基に属します。 (これはオイラーの基準の証明でした)。
結果として、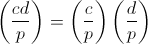 。
。
-1̅は2次剰余ですか? 符号に依存(-1) (p-1)/ 2 pを 4で割ったときに剰余1が得られる場合、 (p-1)/ 2は偶数、 (-1) (p-1)/ 2 = 1 、-1̅は2次剰余です。 pを4で割ると、剰余が3になる場合、すべてが逆になり、-1̅は2次の非剰余になります。
定理の単純な部分: pは、4で割ったときに剰余3を与えます。次に、各括弧内で、 xと-xの項は、-1のルジャンドル記号を掛けることで互いに異なります。つまり、符号が反対で、合計が0になります。 x =0̅を除いて、それらは合計がゼロのペアに分割され、 x = 0 withの項はゼロであり、合計は0です。
pが4で割ったときに余り1を与える場合、 xと-xの項は等しく、それらの合計は偶数です。 したがって、全体の量も偶数であり、括弧内の数値は実際には整数です。 半減後のパリティ/奇数はそれほど複雑ではありません:定理の最初のブラケットには3つのゼロ項があり、残りの項は(p-3)/ 2つのペアに分割され、各ペアの合計は±2です。 4で除算するときの符号を使用すると、剰余は2になり、4で除算するときの全量はp-3と同じ、つまり2になります。半分に除算すると、奇数になります。 定理の2番目のブラケットには、ゼロ項が1つと(p-1)/ 2のペアが2つあり、4で除算した最終余りは0になります。半分に除算すると、偶数が残ります。
したがって、多項式x p-1 -1 =(x (p-1)/ 2 -1)(x (p-1)/ 2 +1)の根はp-1です。 したがって、各ブラケットには(p-1)/ 2のルート(ブラケットの次数の最大可能数)があります。 各二次剰余は、最初のブラケットのルートです( x = c 2の場合、次にx (p-1)/ 2 = c p-1 =1̅ )、それらの(p-1)/ 2があります 。つまり、すべての二次剰余に対して2番目のブラケットが残ります。 したがって、 cのルジャンドル記号はc (p-1)/ 2と同じ残基に属します。 (これはオイラーの基準の証明でした)。
結果として、
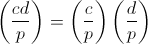 。
。
-1̅は2次剰余ですか? 符号に依存(-1) (p-1)/ 2 pを 4で割ったときに剰余1が得られる場合、 (p-1)/ 2は偶数、 (-1) (p-1)/ 2 = 1 、-1̅は2次剰余です。 pを4で割ると、剰余が3になる場合、すべてが逆になり、-1̅は2次の非剰余になります。
定理の単純な部分: pは、4で割ったときに剰余3を与えます。次に、各括弧内で、 xと-xの項は、-1のルジャンドル記号を掛けることで互いに異なります。つまり、符号が反対で、合計が0になります。 x =0̅を除いて、それらは合計がゼロのペアに分割され、 x = 0 withの項はゼロであり、合計は0です。
pが4で割ったときに余り1を与える場合、 xと-xの項は等しく、それらの合計は偶数です。 したがって、全体の量も偶数であり、括弧内の数値は実際には整数です。 半減後のパリティ/奇数はそれほど複雑ではありません:定理の最初のブラケットには3つのゼロ項があり、残りの項は(p-3)/ 2つのペアに分割され、各ペアの合計は±2です。 4で除算するときの符号を使用すると、剰余は2になり、4で除算するときの全量はp-3と同じ、つまり2になります。半分に除算すると、奇数になります。 定理の2番目のブラケットには、ゼロ項が1つと(p-1)/ 2のペアが2つあり、4で除算した最終余りは0になります。半分に除算すると、偶数が残ります。
パート2.ケースp = 4k + 1。
pを4で割ったとき、剰余1を与えます。定理の最初のブラケットをa 、2番目をbで表します。 aとbが整数であることは既に知っています。
これを証明するために、次の奇妙な量Nを2つの方法で計算します:5つの残基の数( x 1 、y 1 、x 2 、y 2 、t )で、2つの式が同時に満たされるようにします: y 1 2 = x 1 3 -t∙x 1およびy 2 2 = x 2 3 -t∙x 2 。
最初の方法では、最初にtを修正し、 x、yから4の数を計算します。その後、すべてのtの結果を追加します。 固定tの場合、ペア( x 1 、y 1 )は曲線の任意の非特殊点y 2 = x 3 -t∙x 、2番目のペア( x 1 、y 1 )は同じ曲線の任意の非特殊点、そのようなペアの総数は、非特殊ポイントの数の2乗に等しくなります。 (実際、これが奇妙な量を検討している理由です。a2とb 2に近づけることができます。 ) t = 0の場合、方程式y 2 = x 3は既に述べたように、楕円曲線を定義せず、方程式と同数の解を持ちますz 2 = x (ここでy = z∙x )、つまり正確にp t = 1の場合、 p + 2aの解が得られ、 t = g - p + 2bの解が得られます。 他のt値はどうですか?
y 2 = x 3 -t∙xかつcがゼロ以外の剰余の場合、 c 6 y 2 = c 6 x 3 -c 6 t∙xであり、これは(c 3 y) 2 =(c 2 x)と同等3 -c 4 t∙(c 2 x) 。 つまり、 (x、y)がtの方程式の解である場合、 (c 2 x、c 3 y)はc 4 tの方程式の解であるため、解の数はtおよびc 4 tと一致します。 c 4の形のいくつの異なる非ゼロ残基? 一方では、少なくとも(p-1)/ 4 : (p-1)のcの値は4を超えないグループに「結合」できます。一方、 (p-1)/ 4が整数の場合、すべてそのような残差は多項式x (p-1)/ 4 -1の根であるため、それ以上(p-1)/ 4は存在できません。 したがって、正確に(p-1)/ 4個あります 。
したがって、 (p-1)/ 4曲線にはp + 2aの非特殊点があり、別の(p-1)/ 4曲線にはp + 2bの非特殊点があります。 これはすでに必要なすべての半分です。
y 2 = x 3 -t∙xの場合、 g 3 y 2 =(g∙x) 3- (g 2 t)(g∙x) 。 固定xの場合、方程式g 3 y 2 = ...の解の数は2-方程式y 2 = ...の解の数です。 したがって、 t = g 2 (したがって(p-1)/ 4同様の曲線)の曲線上の非特殊点の数は2p-(p + 2a)= p-2aです。 同様に、 t = g 3の曲線上の非特殊点の数は2p-(p + 2b)= p-2bです。
したがって、最初の計算方法は
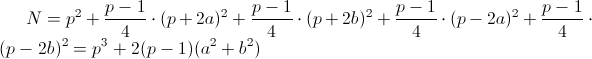
Nを計算する2番目の方法では、まずx 1とx 2を修正し、トリプルの数tとyを計算します。その後、すべてのペアxの結果を追加します。 x 1 = x 2 =0̅の場合、正確にpオプションがあります。yは両方ともゼロでなければならず、 tは任意です。 x 1 =0̅および非ゼロx 2の場合 、 y 1 = 0 である必要があり、 y 2は任意であり、 tは明確に計算され、 pオプションが再び取得されます。 ゼロx 2と非ゼロx 1の状況は対称的です。 最後に、両方のxをゼロ以外にします。 次に、 t = x 1 2- (y 1 2 / x 1 )で、条件(x 2 / x 1 )y 1 2 = y 2 2 + x 2 (x 1 2 -x 2 2 )でペアの数yを計算する必要があります。
x 1 = x 2の場合、方程式はyの2乗が一致するための条件に変わり、 yの異なるペアは1 + 2(p-1)を取得します。 x 1 = -x 2の場合、 pは4で割ったときに余り1を与え、-1̅は2次剰余であるため、状況は似ています。
x 2 / x 1が±1̅に等しくない2次剰余の場合、 c 2 = x 2 / x 1であるような非ゼロのcがあります。 次に(c 2 y 1 2 -y 2 2 )=(c∙y 1 -y 2 )(c∙y 1 + y 2 )= x 2 (x 1 2 -x 2 2 ) 、式c∙y 1- y 2はゼロ以外の任意の剰余であり、 c∙y 1 + y 2を一意に決定します 。したがって、 y 1とy 2を決定します。 合計p-1オプション。
x 2 / x 1が2次の非剰余の場合、楕円曲線と同様に、解の数は2p -2次の剰余の場合の解の数、つまり2p-(p-1)= p + 1です。
まとめます。 x 1 = x 2 = 0で p個の解を与えるオプションが1つあります。 2つの(p-1)オプションがあり、 xの 1つがゼロで、もう1つがゼロ以外の場合、各オプションはp個の解を与えます。 x 2 =±x 1の 2つの(p-1)オプションがあり、それぞれ2p-1の解を与えます。 (p-1)((p-1)/ 2-2)オプションがあり、 x 1は任意の非ゼロの剰余であり、 x 2 / x 1は± 1 1以外の2次剰余であり、これらの各オプションはp-1を与えます決定。 最後に、 (p-1) 2/2オプションがあります。x1は任意の非ゼロの剰余であり、 x 2 / x 1は2次の非剰余であり、これらの各オプションにはp + 1の解があります。 合計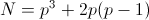 。
。
Nの2つの式を比較すると、証明が完了します。
これを証明するために、次の奇妙な量Nを2つの方法で計算します:5つの残基の数( x 1 、y 1 、x 2 、y 2 、t )で、2つの式が同時に満たされるようにします: y 1 2 = x 1 3 -t∙x 1およびy 2 2 = x 2 3 -t∙x 2 。
最初の方法では、最初にtを修正し、 x、yから4の数を計算します。その後、すべてのtの結果を追加します。 固定tの場合、ペア( x 1 、y 1 )は曲線の任意の非特殊点y 2 = x 3 -t∙x 、2番目のペア( x 1 、y 1 )は同じ曲線の任意の非特殊点、そのようなペアの総数は、非特殊ポイントの数の2乗に等しくなります。 (実際、これが奇妙な量を検討している理由です。a2とb 2に近づけることができます。 ) t = 0の場合、方程式y 2 = x 3は既に述べたように、楕円曲線を定義せず、方程式と同数の解を持ちますz 2 = x (ここでy = z∙x )、つまり正確にp t = 1の場合、 p + 2aの解が得られ、 t = g - p + 2bの解が得られます。 他のt値はどうですか?
y 2 = x 3 -t∙xかつcがゼロ以外の剰余の場合、 c 6 y 2 = c 6 x 3 -c 6 t∙xであり、これは(c 3 y) 2 =(c 2 x)と同等3 -c 4 t∙(c 2 x) 。 つまり、 (x、y)がtの方程式の解である場合、 (c 2 x、c 3 y)はc 4 tの方程式の解であるため、解の数はtおよびc 4 tと一致します。 c 4の形のいくつの異なる非ゼロ残基? 一方では、少なくとも(p-1)/ 4 : (p-1)のcの値は4を超えないグループに「結合」できます。一方、 (p-1)/ 4が整数の場合、すべてそのような残差は多項式x (p-1)/ 4 -1の根であるため、それ以上(p-1)/ 4は存在できません。 したがって、正確に(p-1)/ 4個あります 。
したがって、 (p-1)/ 4曲線にはp + 2aの非特殊点があり、別の(p-1)/ 4曲線にはp + 2bの非特殊点があります。 これはすでに必要なすべての半分です。
y 2 = x 3 -t∙xの場合、 g 3 y 2 =(g∙x) 3- (g 2 t)(g∙x) 。 固定xの場合、方程式g 3 y 2 = ...の解の数は2-方程式y 2 = ...の解の数です。 したがって、 t = g 2 (したがって(p-1)/ 4同様の曲線)の曲線上の非特殊点の数は2p-(p + 2a)= p-2aです。 同様に、 t = g 3の曲線上の非特殊点の数は2p-(p + 2b)= p-2bです。
したがって、最初の計算方法は
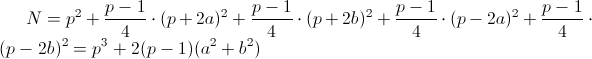
Nを計算する2番目の方法では、まずx 1とx 2を修正し、トリプルの数tとyを計算します。その後、すべてのペアxの結果を追加します。 x 1 = x 2 =0̅の場合、正確にpオプションがあります。yは両方ともゼロでなければならず、 tは任意です。 x 1 =0̅および非ゼロx 2の場合 、 y 1 = 0 である必要があり、 y 2は任意であり、 tは明確に計算され、 pオプションが再び取得されます。 ゼロx 2と非ゼロx 1の状況は対称的です。 最後に、両方のxをゼロ以外にします。 次に、 t = x 1 2- (y 1 2 / x 1 )で、条件(x 2 / x 1 )y 1 2 = y 2 2 + x 2 (x 1 2 -x 2 2 )でペアの数yを計算する必要があります。
x 1 = x 2の場合、方程式はyの2乗が一致するための条件に変わり、 yの異なるペアは1 + 2(p-1)を取得します。 x 1 = -x 2の場合、 pは4で割ったときに余り1を与え、-1̅は2次剰余であるため、状況は似ています。
x 2 / x 1が±1̅に等しくない2次剰余の場合、 c 2 = x 2 / x 1であるような非ゼロのcがあります。 次に(c 2 y 1 2 -y 2 2 )=(c∙y 1 -y 2 )(c∙y 1 + y 2 )= x 2 (x 1 2 -x 2 2 ) 、式c∙y 1- y 2はゼロ以外の任意の剰余であり、 c∙y 1 + y 2を一意に決定します 。したがって、 y 1とy 2を決定します。 合計p-1オプション。
x 2 / x 1が2次の非剰余の場合、楕円曲線と同様に、解の数は2p -2次の剰余の場合の解の数、つまり2p-(p-1)= p + 1です。
まとめます。 x 1 = x 2 = 0で p個の解を与えるオプションが1つあります。 2つの(p-1)オプションがあり、 xの 1つがゼロで、もう1つがゼロ以外の場合、各オプションはp個の解を与えます。 x 2 =±x 1の 2つの(p-1)オプションがあり、それぞれ2p-1の解を与えます。 (p-1)((p-1)/ 2-2)オプションがあり、 x 1は任意の非ゼロの剰余であり、 x 2 / x 1は± 1 1以外の2次剰余であり、これらの各オプションはp-1を与えます決定。 最後に、 (p-1) 2/2オプションがあります。x1は任意の非ゼロの剰余であり、 x 2 / x 1は2次の非剰余であり、これらの各オプションにはp + 1の解があります。 合計
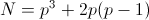 。
。
Nの2つの式を比較すると、証明が完了します。
暗号化はどうですか?
ルジャンドル記号をp回カウントしてaとbを計算するのは実用的ではありません。 Cornacchiaアルゴリズムは、これをはるかに高速に処理できます 。 実際の利点は、a、bの式を反対方向に使用することです。展開p = a 2 + b 2は 、 aとbの順列と符号の変化まで一意であることが証明できるため、 aとbを見つけることは曲線y上の点の数を知ることを意味します2 = x 3 -t∙x非ゼロtの場合、これはp + 1±2aおよびp + 1±2bになります。
曲線上のポイントの数を知ることは、この曲線上の暗号化にとって重要です。 楕円曲線では、ゼロの役割の特別なポイントOを使用して、ポイントを追加する操作(暗号化について少なくとも何かを知っている人なら誰でも聞いているかもしれません)を入力できます。 加算演算に基づいて、自然数による乗算を決定できます: 2P = P + P 、 3P = P + P + Pなど 。 したがって、 nが曲線の次数である場合、任意の点Pに対してnP = Oであることを証明できます。 n、c、dが わかれば 、 x∙(cP)= dPという形式の方程式を解くことができます。剰余の除算に完全に類似しています。高度なユークリッドアルゴリズムは、 c∙x + n∙y = 1 、 x x(cP)+ y∙(nP)= P 、つまりx∙(cP)= P. さらに、 c、dが不明で、 cPとdPが座標で与えられている場合、有効な分割方法は一般に不明です。
与えられた曲線上の点の数を計算することはかなり困難です(多項式アルゴリズムが存在しますが、実際にはかなり遅いです)。 ポイント数に関するいくつかのプロパティを使用して曲線を作成するには、必要なものが得られるまでランダム係数を取り、サイクル内のポイント数を計算しようとしますが、待つ必要があります。 幸いなことに、別の方法があります。
4k + 1の形式の素数と特別な形式の曲線y 2 = x 3 -t∙x (ある意味、任意の非ゼロtの曲線)に満足し、点数p + 1±2aまたはp + 1± 2b 、あなたはそれを取ることができます。 他の曲線はどうですか?
少し後の1911年に、別の著者von Schrutkaが y 2 = x 3 -tの形式、 6k + 1の単純な形式、および表現p = a 2 + 3b 2の曲線について同様の結果を得ました 。 そのため、曲線y 2 = x 3 -t上の点の数を見つけるために、Cornacchiaアルゴリズムが再び可能にします。
証拠について一言
全体としての証明は上記と同様で、 t = 1、g 2 、g 4に対して3つの数字a、b 1 、b 2のみが現れます。ここで、 gは立方体ではなく、それらの合計はゼロであり、平方和が計算されます。 単純な変換の後、必要なものが得られます。
後に、楕円曲線の理論が発展するにつれて、 4p = a ' 2 + d∙b' 2の表現がある場合、 dは自然であり、4で割ると、0または3の剰余が得られ、 pとは互いに素であることが明らかになりました大きすぎると、 pが非常に大きい場合でも、正確にp + 1±a 'ポイントを持つ曲線を効率的に作成できます。 2つの最小値d = 3およびd = 4は、曲線y 2 = x 3 -tおよびy 2 = x 3 -t∙xに対応します。 d = 163の例:
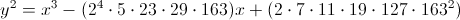
奇数p≠163の場合、この方程式は楕円曲線を定義します。 4pが整数a '、b'でa ' 2 + 163b' 2の形式で表現できる場合、楕円曲線上の点の数はp + 1±a 'です。 そうでない場合は、 p + 1です。 残念ながら、この証明は「ハード」理論を使用しているため、ここではヒントすらありません。
ただし、通常、ラジカルが取得されます。 たとえば、 d = 15の場合 :
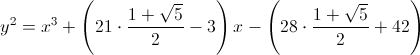 。 4pが合計a ' 2 + d∙b' 2に分解され、 pが d と互いに素である場合、すべてのラジカルが必ず抽出され(たとえば、 d = 15の場合、 c 2 =5̅の剰余cが常に存在します )、次の楕円曲線が得られます希望のポイント数。
。 4pが合計a ' 2 + d∙b' 2に分解され、 pが d と互いに素である場合、すべてのラジカルが必ず抽出され(たとえば、 d = 15の場合、 c 2 =5̅の剰余cが常に存在します )、次の楕円曲線が得られます希望のポイント数。