アルゴリズムの複雑さを知る

この記事では、コンピューターサイエンスで使用されるほとんどのアルゴリズムのランタイムとメモリ使用量について説明します。 過去に、インタビューの準備をしていたとき、私はインターネットでの調査に多くの時間を費やし、検索とソートのアルゴリズムの最良、平均、最悪のケースに関する情報を見つけ、インタビューで尋ねられた質問が私を困惑させないようにしました。 過去数年にわたって、私はシリコンバレーのいくつかの新興企業や、Yahoo、eBay、LinkedIn、Googleなどの大企業でインタビューを受けてきました。インタビューの準備をするたびに、「なぜだれが良いチートシートを作成しなかったのか」アルゴリズムの漸近的な複雑さ？ 「。 時間を節約するために、このようなチートシートを作成しました。 お楽しみください！

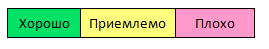
検索する

仕分け

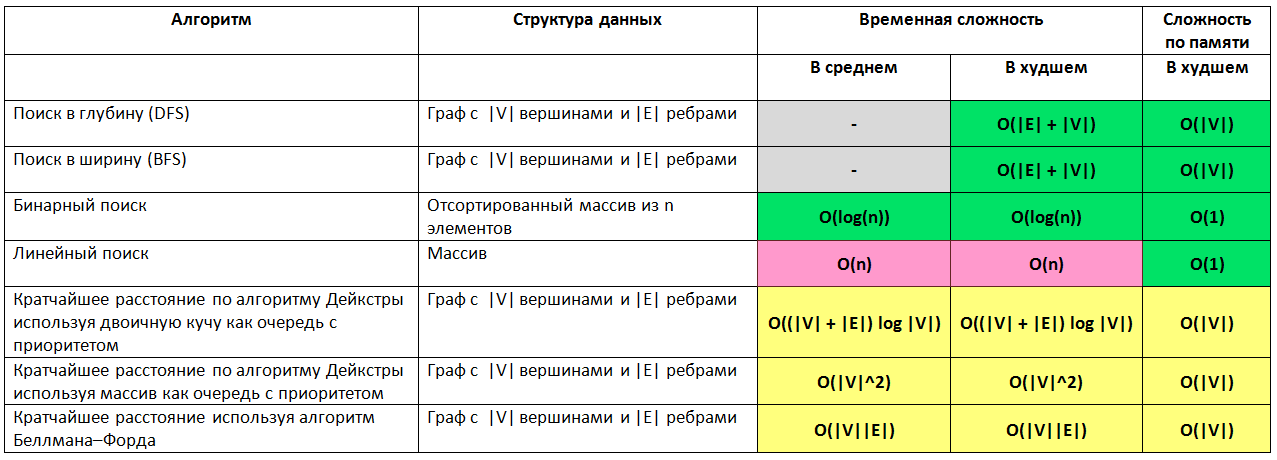
データ構造

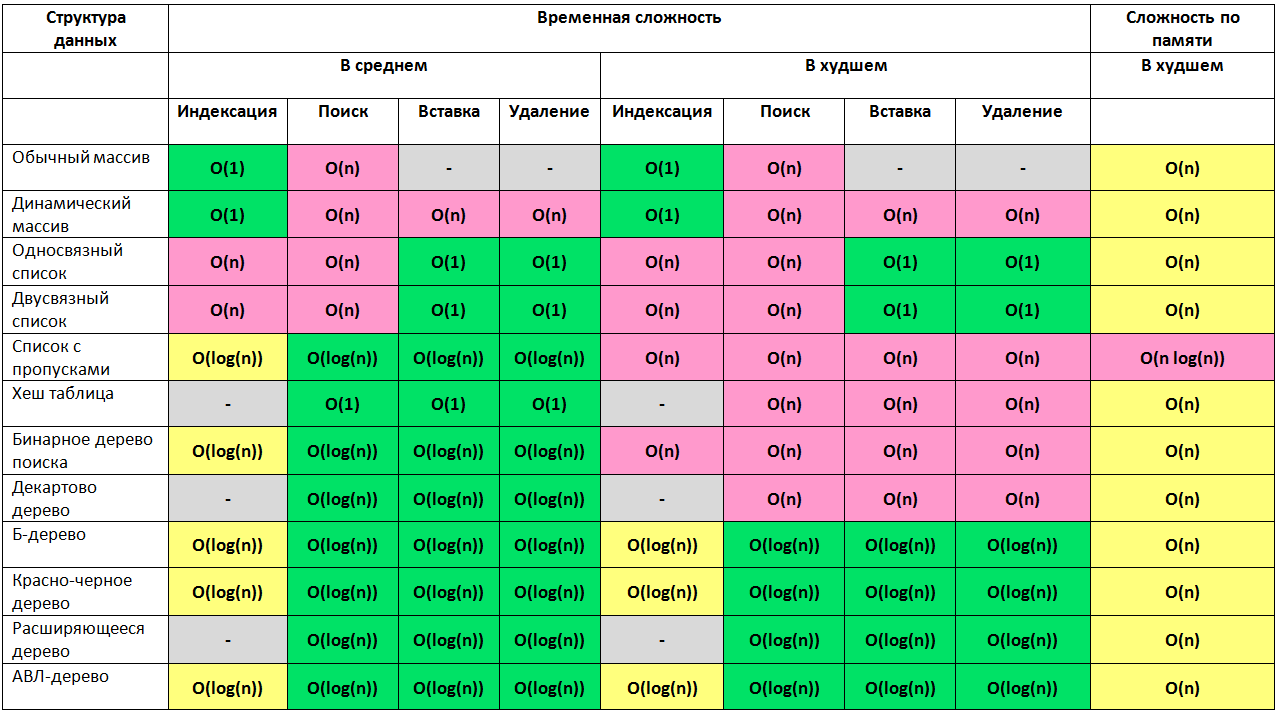
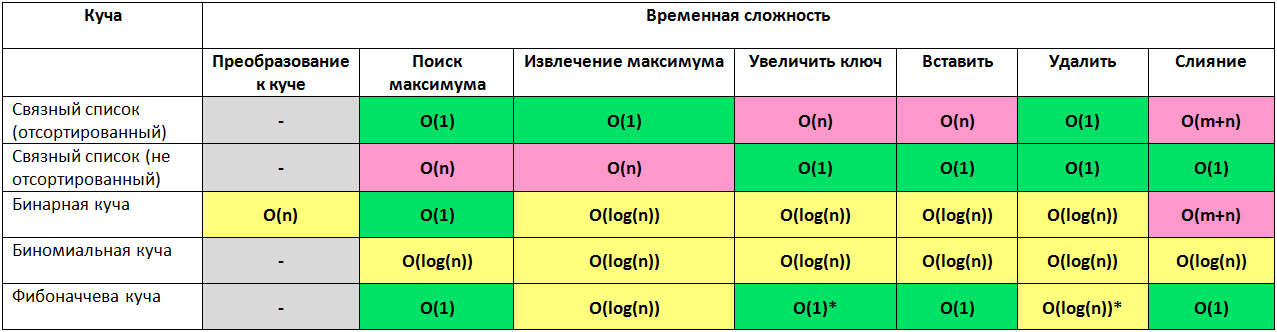
ヒープ

グラフ表示

| V |でグラフを作ろう 頂点と| E | rib骨

漸近的成長記法

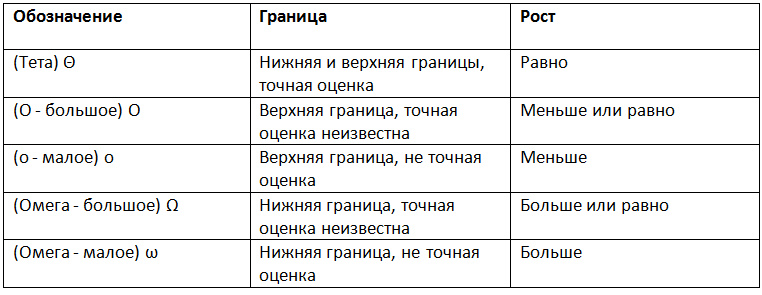
1. （O-大）は上限、（オメガ-大）は下限です。 シータは（O-大）と（オメガ-大）の両方を必要とするため、正確な推定値です（上と下の両方から制限する必要があります）。 たとえば、Ω（n logn）を必要とするアルゴリズムは少なくともn logn時間を必要としますが、上限は不明です。 Θ（n logn）を必要とするアルゴリズムは、少なくともn logn（Ω（n logn））およびn logn（O（n logn））以下を必要とするため、望ましいです。
2. f（x）=Θ（g（n））は、nが無限大になるとfがgのように成長することを意味します。 言い換えれば、成長率f（x）は成長率g（n）に漸近的に比例します。
3. f（x）= O（g（n））。 ここで、成長率はg（n）より速くありません。 O largeは最悪の場合を表すため、最も役立ちます。

要するに、アルゴリズムが__複雑である場合、その効率は__

O成長チャート-大