👣 🧥 🏛️ ゲーム「海戦」：船の配置 📣 🤱🏿 👨🏿‍🎓

こんにちは、愛しい人！ 残念ながら、病院体制のため、先月のゲーム「海戦」のテーマに関する最新の研究を公開できませんでした。 私のメモが誰かに役立つことを願っています。たとえそれが部分的に繰り返されたとしても、それは新しい解釈になるでしょう。

そこで、今日は、戦闘前の（最適ではなく、任意の）船の配置について説明します。左側には、以下で考慮されるアルゴリズムの結果の例があります。文字「R」、「A」、「H」、「B」の形の船は、サイズが5x15の競技場に置かれ、いくつかのセルは使用禁止です（緑色でマークされています）。猫の下で興味を持ってください。

星座の生成は、人工的な敵だけでなく、人にも関係があることに注意してください。比較的同等の戦略的条件を作成するには、ライブプレイヤーの船を擬似ランダムに配置する必要があります。この記事では、有効な配置を見つけることが保証されているアルゴリズムを検討します（この有限時間に費やすことにより、上限推定値を取得できます）。存在する場合（したがって、提案された条件で船舶を配置する基本的な可能性を特徴付けることができます）。

オプションの数

非古典的飛行隊を検討する場合、船配置オプションの総数は次の式で計算されます。

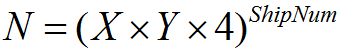
この式は、可能なすべてのオプションを考慮に入れています：先験的な行き止まりです。この式の必要性は、後で受け入れられるように特定の番号を確認するためだけに、各オプションに番号を付けたいという要望が原因です。 10隻の船と10x10フィールドに対して10 ^ 26のオーダーの数が得られることは簡単にわかります。つまり、インデックス付けには、アライメントを考慮して87ビットの変数が必要です。さらに、現場の増加、またはさらに悪いことに、船の数は、状況を悪化させます。したがって、1隻だけを追加すると、オプションの数が約10 ^ 28に増えます。組み込みの（ハードウェアでサポートされる）データ型はどれも、そのような数値を扱うのに適していません。もちろん、大量の算術演算をエミュレートすることもできますが、これにより、パフォーマンスが低下し、ゲームロジックエンジンの1つのタスクに対して不必要に大きな補助ツールが必要になります。さらに、インデックス作成の使用は、各インデックスを一意の配置と一致させることを意味します。つまり、インデックスは、船舶の座標と回転角度を特徴付ける特定の数値セットに「分割」されます。まだ考えてみれば、その後のインデックスの適用の性質を利用して、大量の問題を回避できます。

1隻の船のオプションの列挙

実際、我々は言う：トリプルの数字は船を特徴づけ、そのような「トリプル」のセット-飛行隊。特性を整理すると、次のことを明確にできます。最初の数字は縦座標を特徴づけ、0から（Ymax-1）まで変化し、2番目は横座標で[0;に属します。 Xmax-1]、後者は回転角であり、4つの許可された状態を取ります。少し考えてみると、船の位置と回転を特徴付けるキーがOrdinate-Abscissa-Cornerのツリーの形で想像できます（知覚を簡単にするために1つのデッキがマークされています。作業エリア-2x2フィールド）。

このようなツリーでの深層検索では、値{000}、{001}、{002}、{003}、{010}、{011}、{012} ... {113}が返されます。キーの列挙は、各桁が独自の値の範囲を持つ位置番号システムの数字の列挙に似ていることは簡単にわかります。システムの各ビットは独立しており、船の自由度の1つを特徴付けるため、キー生成アルゴリズムは次の仮想マシンとして表すことができます。

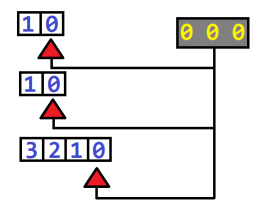
下のレールを移動すると、キー{000}、{001}、{002}、{003}が順番に取得され、その後、レールは「終了」します。低次数がなくなった後、レールを初期状態に戻し、平均を1ポジションシフトします。ジェネレーターは{010}、{011}、{012}および{013}を返します-下位ビットと中間ビットが使い果たされています。排出されたすべての放電の状態を「リセット」し、上部レールを1つの位置{100}、{101}、{102}、および{103}だけシフトします。

したがって、次のキー要求アルゴリズムは次のとおりです。

飛行隊のオプションの列挙

1隻の船に対処したので、私たちは少し自分自身を抽象化し、戦隊の問題を解決できます。キーを生成する原理は同じであり、レールの代わりに、前述のジェネレーターがすでに機能しています。オーバーフローするまで最下位ビット（つまり、ここでは最下位のジェネレーター）のすべての値を順番に並べ替えてから、「次のビットを1つ増やします」（つまり、対応するジェネレーターから新しい値を要求します）して、下位の1つをスクロールします。

{{000}、{000}}

{{000}、{001}}

{{000}、{002}}

{{000}、{003}}

{{000}、{010}}

...

{{000}、{113}}

{{001}、{000}}

...

{{113}、{113}}

星座の生成

それで最後に、最初の問題を解決しました。可能なすべての取り決めを一貫してソートできます。次に、バリアント検証の問題を検討します。

アルゴリズムは簡単です。最初の船のキーを取得し、船を配置できる場合はフィールドに設定して次の船に進みます。それ以外の場合は、この船の次のキーを生成します。キーが終わったら、「より高い」信号を送ります。前の船については、新しい有効なキーを選択し、船を再設置して「戻ります」。すべてが位置システムの数字とまったく同じであり、特定の組み合わせを禁止する制限ルールがいくつか登場しました。

ルールは論理的なカテゴリに便利に分割できるため、必須条件を導入することで検証を高速化できます。たとえば、船は競技場にすべて収まる必要があります。この単純な基準は、上記で検討した事例に関連して、星座の75％を即座に遮断します。さらなるチェックは、実装内のデータの構成に依存します。

事故

これはすべて良いことですが、アクションの決定的シーケンスは、たとえそれらのいくつかが利用可能であっても、常に同じ組み合わせを生成します。解決策は恥ずかしいほど簡単です。ジェネレーターのレール上の数字を混ぜる必要があります。単純に、スタッフからiを読み取り、random_num [i]配列のi番目の要素の値をコールポイントに返します。

配列要素の混合では、以下を推奨できます。

第一に、式は、交換のために、最初とは異なる2番目の要素のインデックスを生成することが保証されています。もちろん、架空の交換random_num [j] <-> random_num [j]を禁止することはできませんが、これに繰り返しを費やすのはなぜですか？

//N –     //% -    unsigned a_indx=rand()%N; unsigned b_indx=(a_indx+1+rand()%(N-1))%N; //      //-  '%' –    //

第二に、完全な混合（乱れ）に最低限必要な量は、

 ceil(N*0.5);

「若い」レールと「良い」ジェネレーターで数字を混在させる例を以下に示します。

この場合、交換を2回繰り返して混合を完了しました。注：このジェネレーターは、元のジェネレーターと同様に、キーのセット全体を返しますが、異なる順序で、ケースごとに異なる配置を作成できます。「ランダム性」は主に主観的な概念であり、自然のままのスラットはランダムと見なすことができます。

前のシリーズ

（誰かに言及するのを忘れた場合は謝罪し、PMに通知します）

おわりに

この記事を読んで時間を割いて、この記事をマスターした皆さんに感謝します。私は質問に答え、批判についてコメントしようとします。リクエスト：記事の主題から議論をそらさないように、PMで校正のためのコメントと提案を書いてください。

ゲーム「海戦」：船の配置