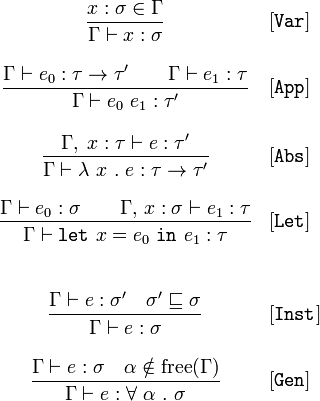
ただし、この中国語の文字の意味を明確にする前に、原則として、なぜこれが必要なのかを理解する価値があると思います。 Daniel Spivakのブログ投稿 ( translation )は、Hindley-Milnerアルゴリズムの究極の目標について、その応用の詳細な例に加えて、本当に良い説明を提供しています:
機能的に言えば、Hindley-Milner(またはDamas-Milner)は、それらがどのように使用されているかを考慮した型推論のアルゴリズムです。 文字列は、サポートする機能を通じて型を推測できるという直感的な知識を形式化します。
そのため、特定の式の型推論アルゴリズムを形式化します。 この投稿では、「何かを形式化する」とはどういう意味かを説明し、Hindley-Milner形式化の「ビルディングブロック」について説明します。 第二部では、これらのブロックのより具体的な説明をします。 最後に、パート3では、StackOverflowからの質問を翻訳します。
フォーマライズとはどういう意味ですか?
それで、表現について話しましょう。 自由な表現。 どの言語でも。 これらの式の型推論についても話したいと思います。 そして、型を推測できるルールを見つけたいと思います。 次に、これらのルールを型推論に使用するアルゴリズムを作成します。 そのため、メタ言語が必要です。 その助けを借りて、任意のプログラミング言語での表現について話すことができるようになります。 このメタ言語は次のことを行う必要があります。
- 内容を気にせずに、 フォームのみに基づいて型推論のステートメントについて話すことができるように、抽象的かつ一般的であること(したがって、 形式化 )
- 式が何であるかを正確かつ明確に、しかし直感的に定義する
- 少数の議論の余地のない原始的な概念の観点からこの定義を与えること
- 同様に、型の定義、式に型があるという考え、この式に特定の型があると推定できるという考えを示します
- シンプルで簡潔な象徴的表現に屈する。 つまり 「最初の式を2番目の式に適用することによって形成される式は、文字列からこのコンテキストに特化する必要のない何らかの型の関数型を持っている」と言う代わりに、「
e
1 (e
2 ):String
→t
" - 型推論を完全に自動化できるように、コンピューターが理解して実装できるものに簡単に変換できます
上記の詳細を説明するために、非常に短い形式化の例を見てみましょう。 任意のプログラミング言語で式の種類の派生について話すために言語を形式化する代わりに、任意の自然言語でステートメントの真理について話すために言語を形式化する場合はどうでしょうか。 形式化せずに、次のように言うことができます。
雨が降った場合、ボブはいつも傘を持っていることを知っていると仮定します。
そして今、雨が降っていることを知っているとします。
したがって、私はボブが傘を取ったと結論付けることができます。
そして、同じ形式の議論は、そのような結論に対して有効です。
命題計算は、これらすべてをModus Ponensとして知られる規則(「推論規則」)の形式で形式化します。
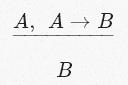
ここで、
と
は、任意の自然言語でのステートメント(別名、文または条項)を表す変数です。
次に、Hindley-Milnerの形式化の構成要素をリストします。
正式なビルディングブロック
以下が必要です。
- 式について話す正式な方法。 この形式化は上記の基準を満たさなければなりません。 この目的のために、 ラムダ計算を使用します。 すぐにすべてを説明しますが、超自然的なことは何もありません
- 型について話す正式な方法、および型と式を一緒に話す正式な方法。 最終的に、Hindley-Milnerアルゴリズムの目標は、「式
e
型がt
」のような結論を導き出すことができるようにすることです - 他のステートメントを介して式のタイプに関するステートメントを取得するための正式なルールセット。 これらのルールは次のとおりです。「ある式が1つのタイプを持ち、他の式が2番目のタイプであることを既に実証できる場合、3番目の式には3番目のタイプがあります。」 このルールのセットは、StackOverflowの質問で見たとおりです 。 完全に翻訳します
- アルゴリズムは、開始点から必要なステートメントを導き出すために、推論ルールを合理的に使用する必要があります:「関心のある式
e
はt
型です」。 「Hindley-Milner algorithm」というフレーズの「アルゴリズム」の部分がこれに責任があり、これらの投稿ではこの問題について議論するつもりはありません。
さあ、行こう!
翻訳者のメモ:翻訳に関するPMのコメントに非常に感謝します。