デジタル信号の平滑化

はじめに

post habrahabr.ru/post/183986によってこの記事を書くことを余儀なくされました。画像を平滑化するためのアルゴリズムが正しく使用されていません。



すぐにポイントを取得しましょう。



デジタル信号の数学モデル—要素が数字であるベクトルと行列。 数値には、バイナリ（バイナリ信号）、10進数（「通常」信号）などがあります。 音声、画像、ビデオはすべてデジタル信号^1に変換できます。音声はベクトルに、画像はマトリックスに、ビデオは一連のマトリックスに変換されます。 したがって、デジタル信号は、情報を提示するための普遍的なオブジェクトです。



平滑化タスクは、実際には、痙攣性（ステップ）変化から信号をフィルタリングするタスクです。 有用な信号にはそれらは含まれないと考えられています。 多くの鋭いが振幅が小さいレベル低下による段階的な信号には、平滑化された信号にはない高周波成分が含まれています。 したがって、いくつかの平滑化アルゴリズムでは、まず、さまざまな周波数成分がどのように大きく減衰するかを判断する必要があります。 つまり、対応するフィルターの振幅周波数特性を構築する必要があります。そうしないと、アーチファクトが「実行」される可能性が高くなります。



平滑化タスクは、信号を間引く場合、つまり、たとえば小さな画面に大きな画像を表示する必要がある場合に使用できます。 または、サウンドのサンプリング周波数が、たとえば48000 Hzから44100 Hzに低下した場合。 サンプリング周波数を下げることは、予備の信号処理（ローパスフィルター処理）を必要とする潜行的な操作ですが、これは別の議論のトピックです...



「悪い」平滑化の例を挙げましょう





通常の平均化と出力信号は「スムーズ」である必要があります。 しかし、彼がどれくらい「スムーザー」になったかをどのように判断するのでしょうか？ 行き過ぎた？ または、1/3ではなく選択するいくつかの要因がありますか？ それとも5点以上の平均？ 信号の周波数成分がどの程度減衰するかを判断する方法は？ 最適な（つまり、特定のタスクに）見つける方法

「普通の」プログラマーが自分のアルゴリズムを実証できるように、これらの質問や他のいくつかの質問に答えようとします 。

信号

このセクションでは、信号はベクトル、つまり特定の数の配列です。 たとえば、4つの要素のベクトルs =（2,5; 5; 0; -5）。



簡単にするために、10進数の実数のみが考慮されます。



最も一般的で理解可能な信号の1つはデジタル化された音です。 信号サイズは、音の持続時間とサンプルが取得される周波数（サンプリング周波数）に依存します。 要素信号数は、デバイスのサンプリングと保存によって測定される音の現在の振幅に依存します。



すでに述べたように、スムーズにする最も簡単な方法の1つは

（1）

ここで、 sは元の信号、 vは平滑化された信号です。



方法（1）は、合計の平滑化特性に基づいています。これは、多くの乱数の合計として計算される平均値が、合計数の増加とともに、ランダム変数^2のようにどんどん少なくなることは誰にとっても明らかであるためです。 。



しかし、式（1）で係数を選択する根拠は何ですか？ 平均は何に計算されますか？ はいのようですが、...そして、あなたが3つの用語ではなく、16の用語を取るなら？ そして、32 ??。なぜ中心要素s [i]からますます遠く離れたサンプルが同じ重量で取られるべきですか？ 結局のところ、サンプル間の距離⁴が増加すると、サンプル間の接続は徐々に弱くなることが判明するかもしれません。



「スイカ」という単語の発音の例を10回続けて検討し、記録された信号のサンプル間の関係を追跡しようとすると、ますます分離されたサンプル間の関係の弱体化を見つけることができます。 当然、「長距離」を考慮すると、同じ単語の繰り返しにより音が繰り返され、依存関係が再び増加および減少する、などなどです。 しかし、原則として、ノイズは単語、フレーズ、文ではなく個々の音の近くに現れるため、平滑化するときに「長距離」を考慮しません。 単語またはフレーズのレベルでのノイズは、明らかに人工的（効果音）またはエキゾチックな自然（エコー）です。 これはすでに「非ランダム」ノイズであり、別途調査が必要です。 ここでは、「純粋な」ノイズを考えます。これは、簡単に言えば、うるさくうるさく、有用な信号とはまったく異なります。



単純な推論に基づいて、（1）の項の数（フィルター次数）は、隣接するサンプルが互いにどれだけ密接に依存しているかに依存することが明らかになります。 たとえば、次々に続くサンプルが10個だけの依存関係がある場合、30次のフィルターを使用しても意味がありません。 実際、それは「意味がない」ということすらありませんが、-読み取り値が実際に接続されていない場合、有用な信号の過剰な平滑化が開始されるため（音節の「食べる」）不可能です。 しかし、ここでの3次フィルターは、既に述べたように、10個の隣接サンプルの次数の依存性が観察されるため、有用な信号に関する情報の使用に関して最適ではありません。 したがって、9次のフィルターを使用して「運を試す」ことができます。もちろん、プロセッサーコンピューターの負荷が増加します。 ここでは、おそらく実験的に決定する必要がありますが、このゲームはキャンドルの価値がありますか？..



隣接するサンプルがどの程度密接に関連しているかを推定する方法は？ 自己相関関数（ACF）を計算します。 希望する人は、さまざまな単語、フレーズ、フレーズの繰り返し、およびその後のACFの構築に関する実験を行うよう招待することができます（たとえば、Matlabプログラムを使用すると、コードや式をあまり考慮せずにこれを行うことができます）。



では、（1）のフィルター係数をどのように選択しますか？



この場合、単一の効果、つまり次の形式の信号に対するフィルターの応答を考慮すると便利です。





たとえば、フィルター（1）は次の応答（インパルス応答）を返します



平滑化後、信号の持続時間は3つの要素に等しくなったと結論付けることができます。 5つの要素のフィルターを使用する場合？..そうです、出力信号の持続時間は5つの要素に等しくなります。 これがどれほど役立つかは、特定の状況（タスク）によって決まります。



ところで、待望のアーティファクトはすでにそこにあります！ インパルス応答（1）は、本質的にはまったく滑らかではない長方形のインパルスです！..奇妙なことですか？ また、5ポイントフィルターを使用する場合はどうなりますか？ 次に、出力ではより長い矩形パルスを取得しますが、振幅は小さくなります。 うまくいきません...最も単純なテストでは、単純な平均化は平滑化には適さないと言われています。



フィルター（1）を周波数側から見てみましょう（既に一時的なフィルターを見ています）。



信号が音声の場合、高調波信号のセット⁵ （「正弦波」）によってかなり適切に記述され、特定の正弦波の減衰の程度はその周波数に依存します。 繰り返しますが、スムージングフィルターを正しく選択すると、有用な正弦波が完全に消えることはありません。つまり、動作周波数範囲でのフィルターの振幅周波数特性はかなり均一になるはずです。



サンプリング定理の限界を超えることなく、当然ながら、特定の周波数の1つのシングルトーン信号を考慮してフィルターを通過させてみましょう。 時間離散化ステップT _dを1に等しくする、つまり、サンプルを1秒単位で取得します。 周波数f = 1 /（3 T _d ）= 1/3 Hzの信号を取得します。





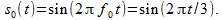
2つの期間に限定





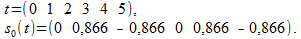
フィルターの応答（1）は次のようになります





奇妙なことに、ほとんどゼロになりました...有用な信号の一部の成分を失う可能性があることがわかりました。



わずかに高い周波数の信号に対する応答を確認します





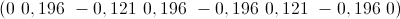
ご覧のとおり、波形は失われていません。 問題は何ですか？..



実際、フィルター（1）の振幅周波数特性は、動作周波数帯域（サンプリング周波数の0から半分までの帯域）で単調ではなく、サンプリング周波数の3倍低い周波数で1つのゼロを持っています。 見せ方は？



簡単に言えば、フィルターの周波数応答を決定するには、フィルターの出力でのスペクトルと入力でのスペクトルの比を見つける必要があります。



入力での信号s [ i ] のスペクトルをS （ f ）と表し、1クロックサイクルT _dだけ遅延した信号s [ i -1]のスペクトルは、元の信号のスペクトルを通して次のように表されます。

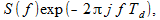（2）

ここで、 jは虚数単位です。



高度な信号s [ i +1] のスペクトルは、次のように表されます。

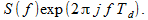（3）



虚数単位とはどういう意味ですか？ そして、どうすれば（2）と（3）を正当化できますか？

サイン、コサイン、指数の有名な[1、2]シリーズを書くと

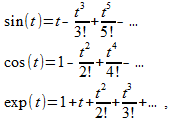（4）

次に、 j ² = -1のような数値jを選択します。最初の2つを通して最後の行を表現できます

（5）

つまり、虚数指数を持つ指数を介して、任意の複素数を書き込むことができます。 数（5）のモジュールは1（虚数部と実数部の平方和の平方根）に等しいため、（5）の形式で複素数を書き込むには、モジュールで除算して乗算する必要があります

（6）



（5）および（6）から、ある実数を掛けた虚数単位を指数で区別できる場合、この数は複素数の引数になります。



この場合、信号が考慮されるため、複素数の振幅モジュールは高調波信号の振幅に対応し、引数は位相に対応します。 たとえば、次の形式の信号を取る場合

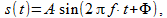（7）

振幅Aと位相Fを区別できます。係数 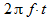-これもフェーズであり、場合によっては括弧で囲まれません。 たとえば、信号（7）が何らかのフィルターを通過する場合、特定の周波数fでフィルターが導入する入出力の信号の位相差を知ることが重要です。



信号（7）がt _0の値だけ遅延される場合、同じ信号が取得されますが、一定値だけ位相がシフトします

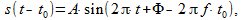（8）

つまり、任意の信号が遅延すると、その周波数成分はすべて、現在の周波数と遅延値に依存する量だけ位相シフトします。 これにより、式（2）および（3）を説明できます。 したがって、任意のアルゴリズムを分析する場合、 位相周波数特性も重要です。これは、入力信号の各周波数成分がフィルター（アルゴリズム）を遅延させる時間を示します。 通常、低周波数と高周波数では、フィルターの遅延が異なります。



（1）、（2）、（3）から、フィルターの周波数応答（伝達関数）は次の形式になります。

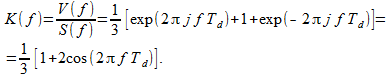（9）



出力信号のスペクトルは入力のスペクトルを通じて直線的に表現されるため、出力（9）の場合、入力信号のスペクトルは正常に低減されます。 さらに、フィルター（1）の周波数応答は実数であることに注意してください。つまり、このフィルターは位相歪みを導入しません⁶ 。 式（1）の対称性により、（おそらく無意識に）これを達成しました。フィルター出力の各サンプルは、現在のサンプルと2つの隣接サンプルの合計に等しくなります。



物理的に、このようなアルゴリズムは、先頭のサンプルを使用するため、ストレージデバイスが存在する場合にのみ実装されます（サンプルs [ i ]を計算するには、サンプルs [ i +1]が必要です）。 これは現在大きな問題ではなく、原則として、対称アルゴリズムを使用しています。 位相歪みが有用であることが判明した場合、主なことは、意識的にアルゴリズムを適用し、異なる角度からそれを見ることです：周波数と時間。



（9）の周波数依存性をプロットすることは難しくありません。 簡略化するために、正規化された周波数f ₀ = f T _dを導入します。その変動の有効範囲は[0 ... 0,5]です。 サンプリング定理によるサンプリング周波数の半分よりも高い周波数の信号成分は存在しないはずです（デジタル化する前に、信号は対応するローパスフィルターを通過します）。 サンプリングレートは、デジタルデバイスによって1秒あたりに送信されるサンプルの数を示します。 たとえば、1サイクルT _dが1ミリ秒に等しい場合、1秒間に1,000個のサンプルを発行する必要があります。



（9）を分析すると、一定の間隔で、伝送係数はゼロより小さく、振幅は定義により正の量であることがわかります...状況から抜け出す方法は、位相特性のマイナス記号を削除することで伝達関数モジュールを構築することですが、それでも定数ではありません（ゼロ）。 「マイナス1」という数をとると、式（5）で表すことができます。

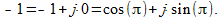（10）

つまり、単位モジュールと180度（pi）の位相を持つ複素数です。



したがって、一部の「高」周波数に対する3点対称アルゴリズム（1）は、180度の位相シフトを導入します。つまり、単に入力信号を反転させます。 この効果は、2/5 Hzの正規化された周波数に対する上記の応答を分析することで確認できます。





図 1. 3点対称平滑化アルゴリズムの振幅周波数特性と位相周波数特性 （1）



図から 図1では、1/3の周波数の信号はこのアルゴリズムによって抑制され、1/3を超える周波数の信号は反転します。 したがって、有用な動作周波数範囲を[0 ... 0.5]から[0 ... 1/3]に安全に削減できます。 伝達係数の急激な低下に満足できない場合は、より矩形の振幅周波数特性を持つ別のアルゴリズムを決定する必要がありますが、同時にどの位相がまだ不明なのか...



実際、得られた非単調な周波数応答は、インパルス応答の矩形形状の結果です...、0、0、...、1 / 3、1 / 3、1 / 3、0、0、... したがって、インパルス応答は、アルゴリズムの重大な欠陥に簡単に気付く方法です。 周波数応答は、計算が複雑であるにもかかわらず、より微妙な欠陥に気付き、除去できるという点で便利です。



アルゴリズム（1）をより一般的な形式で記述すると

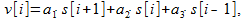（11）

次に、周波数応答の知識に基づいて、次のように係数を選択することができます。

そのため、振幅周波数特性は、動作周波数範囲（0〜0.5）で単調になります。 このためには、少なくとも、動作範囲内にゼロがないことが必要です。



遅延サンプルs [i – 1]を先行s [i + 1]と区別する理由がないため、係数a ₁とa ₃を同等と見なします。 透過係数を書き留めた後

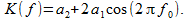（12）



最初のゼロを周波数f ₀ = 0.5に移動してみましょう。 このためには、等式a ₂ = 2a _1を満たす必要があります。つまり、サイドサンプルの重みは中央のサンプルの半分になります。 次に、より最適なアルゴリズムは次のようになります

（13）



（13）で₁つの係数a ₁を選択する方法



パルス過渡応答の観点からアルゴリズム（13）を見てみましょう。 これを行うには、単一のジャンプに対する応答を見つけます ：

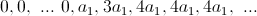（14）



ご覧のとおり、定常状態の出力振幅を1に維持するには、係数a ₁ = 1/4を選択する必要があります。 つまり、すべての係数の合計は1に等しくなければなりません。



最後に、完成したアルゴリズムの

（16）

周波数特性（振幅と位相）を構築することができます（図2）。





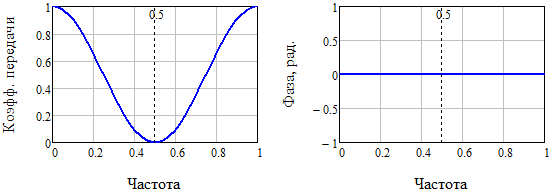
図 2. 3点対称平滑化アルゴリズムの振幅周波数と位相周波数の特性（16）



分析図 図2は、位相歪みが消え、動作周波数帯域[0 ... 0.5]で振幅特性が単調になったことを示しています。 ある意味では、3ポイントフィルターからすべてを絞り出しました。



特に、多くの平均化されたサンプルがある場合、単純な平均化は常に最適とはほど遠いことが明らかになりました。

画像

画像に関しては、ある程度まですべてが信号の場合と同じです。振幅と位相の歪み、インパルス応答、信号エネルギー-主な違いは、ベクトルの代わりに行列が使用されることです。 また、画像には時間座標はありませんが、空間の座標があるため、空間サンプリング周波数があることに注意してください。 この違いは、アルゴリズムの数学にまったく影響しないため、かなり形式的なものです。



次に、隣接するポイントによって画像を平滑化するための「最も簡単な」アルゴリズムを考えます（図3）。 フィルター出力でカウントv ₀₀

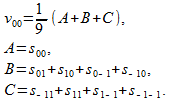（17）





図 3.隣接点で画像を平滑化するスキーム



式（17）では、3つの項A 、 B、 Cが特別に区別されます。これは、 BとCの 4つの対応する内部項が中央参照s ₀₀から独自の距離を持っているためです。 ここでは、用語Aが最大の重みを持ち、次にBとCが降順であると仮定するのが自然です。



画像の場合、スペクトルと透過係数は2次元になります。つまり、2つの周波数に依存します。最初の周波数は水平、2番目の周波数は垂直です（明確にするためにすべてが条件付きです）。



フィルター（17）の透過係数は次のとおりです

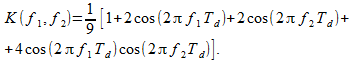（18）



たとえば、約30の離散的な周波数を使用して、周波数応答モジュール（18）の等高線グラフを作成すると（図4）、図4のような歪みが見られます。 1.左下隅は最低周波数に対応しています。 サンプリング周波数の1/3の周波数で周波数応答にディップがあります（この場合のサンプリング周波数は両方の座標で64です）。





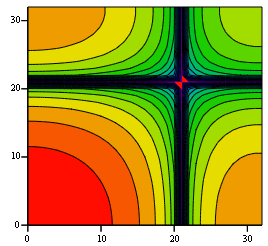
図 4. 9点対称平滑化アルゴリズムの振幅周波数特性 （17）



図のサンプルの係数をシャッフルします。 3、次の平滑化アルゴリズムを取得できます

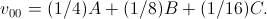（19）



さらに、単一の露出が画像の中央に配置されている場合、フィルター（19）の応答は次の形式になります。

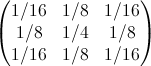（20）



実際、（20）はフィルターのインパルス応答です（残りはゼロなので、これらは9つの主要なカウントです）。 インパルス応答のすべてのサンプルの合計は1に等しくなります。 フィルター（19）の周波数応答は、図3 5。





図 5. 9点対称平滑化アルゴリズムの振幅周波数特性 （19）



ここでも、通常の平均化アルゴリズムの改善が見られます（図4と図5を比較）。

まとめ

デジタル信号（スムージングなど）を処理するアルゴリズムを開発する場合、単純な平均化のような直感的なアルゴリズムを信頼するべきではありません。



より一般的なアプローチは、加重加算の手法です（サンプルに定数を掛けただけで、結果が加算される場合、線形アルゴリズムのみが考慮されました）。



重みの合計は、小さな重みが中心要素からより遠くに設定されている場合、統計的に（距離の増加に伴う依存性の弱体化の自然な性質）および機能的に（振幅-周波数特性の単調性を確保して、厳密に数学的に係数を選択することが可能です）正当化されます。



大きな役割は、加重和の係数によって決定されるフィルターの振幅-周波数特性によって果たされます。 特定のフィルターが特定の周波数範囲を通過し、別の周波数範囲をブロックすることを証明できます。 さらに、通過帯域、障害物などの不均一性を判断することができます。 フィルターの次数が大きいほど、自由度が大きくなり、振幅周波数特性の形状をより適切に選択できるようになります。



重要な役割は、主にアルゴリズムの対称性の程度によって決定される位相周波数特性によっても果たされます。 リアルタイムアルゴリズムは、最初のサンプルが到着した瞬間にフィルター出力にカウントダウンが表示される場合、対称ではないため、均一な位相応答（一定、多くの場合「ゼロ」）を提供できません。 このようなアルゴリズムは、入力信号に遅延を導入します。たとえば、一般に、平滑化された画像は両方の座標でシフトします。 画像が複雑な場合（つまり、多くの周波数成分を持っている場合）、位相の歪みは、座標をシフトするだけでなく、著しく歪める可能性があります。これは単純な画像の場合にほぼ当てはまります。



また、特定のアルゴリズムに対応するフィルターのインパルス応答にも注意を払う必要があります。これにより、信号の時間スケールまたは画像の空間座標のスケールで、フィルターを直接見る簡単な方法が可能になります。



そして最後に、対応するフィルターの出力での信号損失を決定するために、アルゴリズムのエネルギー分析が必要です。この分析は、パルス過渡応答のフレームワークで便利に実行されます。

脚注

1. ,

2. ,

3. , , — , , …

4. —

5. , , «»

6. ,

ソース

1. [ ], : , ru.wikipedia.org/wiki/%D2%F0%E8%E3%EE%ED%EE%EC%E5%F2%F0%E8%F7%E5%F1%EA%E8%E5_%F4%F3%ED%EA%F6%E8%E8

2. [ ], : , ru.wikipedia.org/wiki/%DD%EA%F1%EF%EE%ED%E5%ED%F2%E0