私が年をとったとき、私はすでにコンピューター画面に同じパターンを表示したかった。 長い間、どの式を描くかに従って、それをどうやってやるのか考えていました。 それまでは、この式は私なしで派生したものだと思い、 ウィキペディアにも載せました-描きたくありません。 結論の主な考え方は、小さな円がスリップせずに大きな円に沿って移動するため、小さな円から点が移動する距離は、大きな円の対応する距離に等しくなければならないということです。
しかし、奪われた要塞はもはや引き付けられません。 タスクを一般化するのは今では自然です。たとえば、小さな円を円ではなく、より複雑な形状、たとえば楕円の中に乗せます。
しかし、その後、ウィキペディアからの結論が円周の下で正確にはっきりしていることが突然明らかになります。 他の数字については、すぐに3つの障害に遭遇します。
まず、円は単純な図形であり、その長さを計算するのは非常に簡単です。回転角度に半径を掛けると、完了です。 しかし、楕円の長さは、より複雑なものは言うまでもなく、特別な種類の積分であり、「楕円関数」という独自の名前さえ持っています。 そして、この非傾斜積分-つまり、初等関数では表現されません。 そして、デリバティブを通して楕円の長さを考慮し、さらにそこに式がパラメトリックであることを考慮することは、小さな喜びです。 つまり、プログラムすることはもちろん可能ですが、計算は非常に長く実行されます。
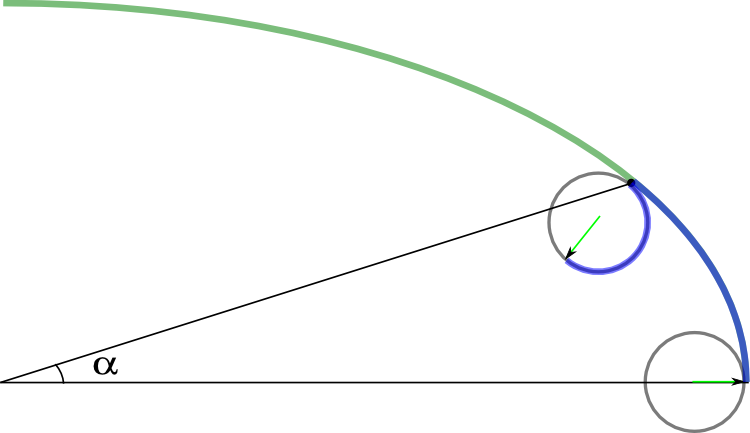
第二に、円は一定の曲率の図形です。 したがって、円の接点と大円の中心の間の線は常に小円を通過するため、式の導出が簡単になります。 楕円(および曲率が変化する他の曲線)の場合、これらのポイントは氷上の牛のように異なる方向に移動します。 これがイラストです。
3番目の問題については、後で説明します。
しかし、心はすべての障害を克服します。 まあ、またはほとんどすべて。 ウィキペディアから移動距離の等しさの主なアイデアを採用し、2番目のアイデアはギアの穴の位置を、大きい円に対する小さい円の中心の位置と小さい円に対する穴の位置の合計として計算することです。
したがって、上の図をもう一度見てください。 デカルト座標と極座標(両方を使用する必要があります)の中心は1か所にあります。メイン楕円の中央で、x軸から反時計回りに極角を測定します。 小さな円の上に、特に美しさのために緑の矢印が描かれました。 最初は、角度が0の場合、この矢印が0の角度になるように小さな円が立てられ、大きな円との接点がx軸上にあります。
これで、原点から見たときに接線のポイントが角度αのポイントに移動するように、ホイールが回転しました。 この間、矢印の端は何らかの方法で移動し、このパスは楕円上の対応するパスと等しくなります(図では両方とも青色でマークされています)。
少しシーンを見てみましょう。
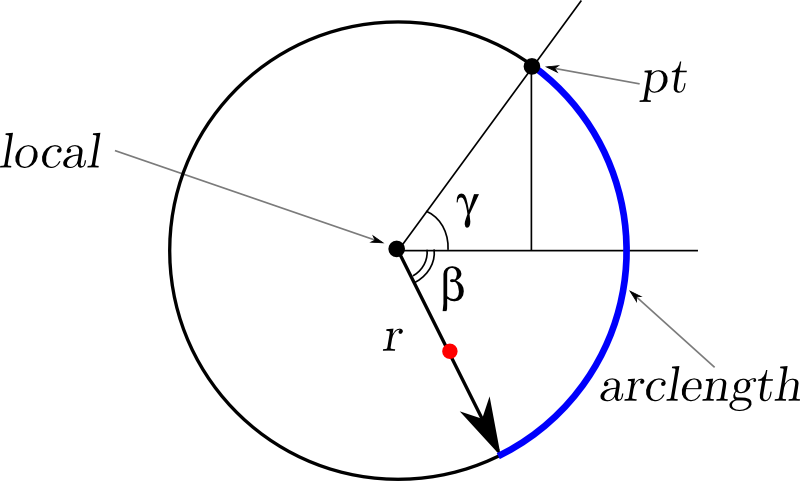
ここでは、同じ接触点(ptとしてマーク)、ホイールの矢印(太字で描画)、この矢印の端までの軌跡(青で強調表示)、同時にホイールの穴(赤い点)を確認します。 localはホイールの中心であり、この時点でローカル座標系の中心が配置され、これを使用して穴の位置が計算されます。
したがって、ポイントptは楕円の中心から角度αで見えます。 この点の座標を見つけるのは簡単です-楕円と対応する線の交点のように。 さて、ホイールの中心の座標を知っておくといいのですが、そのためには角度γ(ホイールの中心から接触点までの方向)を知る必要があります。 ああ! -キーワード「touch」。 曲線がそれらに接触する点で、共通の接線を描くことができ、必要な角度はこの接線の角に垂直になります。 接線角度の接線は、ある点での楕円の導関数です。 この導関数を計算するだけです。
もちろん、楕円のパラメトリック方程式を取得し、そこから微分公式を取得できます。 しかし、これは非常に不便です-パラメータは既知の量とは関係ありません。 そして、楕円を別のものに置き換えるとどうなりますか?
物理学者は、主なる神には、肉体に直接生を統合できるという重要な利点があると冗談を言っています。 これが使用する方法です。
デリバティブとは何ですか? 単純な集団農場の方法で、限界への通過を除外する場合、これは変数の値の変化に対する関数の値の変化の比率です。 私たちはコンピューター上でプログラムを作成しているため、限界遷移によって暗示される無限大はありません。私たちの世界は離散的であり、そのような式は私たちに非常に適しています。 したがって、前のポイントを覚えて、比率(Ypt-Yprev)/(Xpt-Xprev)を計算するだけです。 ポイントを取る頻度が高いほど、計算はより正確になり、最終的には誰も実際の微分と区別しなくなります。
さて、それは簡単です-角度γとそれに沿ったホイールの中心の座標を見つけます。
ローカル座標で穴座標を見つける方法は? このために知っておく必要があるのは、角度βがホイールを回したことだけです。 直接計算することはできませんが、接点と矢印の端点の間の角度に等しく、そこから既にわかっている角度γが差し引かれます(図を参照)。 ホイールは時計回りに回転し、角度は反時計回りに測定されるため、結果を反対の符号で取得することを忘れないでください。
大きな角度を見つけるには? それほど難しいことではありません-青い弧の長さをホイールの半径で割るだけです。 そして、青い弧の長さは、楕円弧の対応する部分に等しくなります。
ああ、ここでは恐ろしい楕円関数が私たちを待っています。 しかし、導関数の場合と同じようになります-曲線の長さを、現在の点と前の点の間の短い線で構成されるポリラインの長さに置き換えます。
さて、残りは単純です-ローカル座標系で赤い点の座標を見つけ、それらをグローバル座標系に再カウントします。
次に、3番目の問題について。 ウィキペディアは、大小の円の半径を設定し、それらの比率が合理的である場合、曲線は必然的に閉じられると予測します(なぜ開いた曲線が必要なのですか?美しくない)。 これも行うことができますが、それは役に立たない-楕円の長さは無理数で表現され、半径はなく、曲線は閉じられない可能性が高いです。
少し異なる方法で行います。ホイールが楕円を何回通過するか、そして今度はホイールが何回回転するかを設定します。 これらのデータに基づいて、曲線が閉じるように、ホイールに必要な半径を計算します。 ここでは、パスがすべて同じであることが役立ちます。
今、長い計算の後、最終的に芸術的な結果を楽しむことができます。 どれだけきれいか見てください:

図の黄色の円は車輪であり、外部の黒い楕円は私たちが乗る円であり、黄色の楕円は車輪の中央の経路です。
ところで、結果のアルゴリズムは楕円のプロパティから完全に独立しているため、外部曲線は閉じたままであれば、必要に応じて変更できます。 あなたも...広場を取ることができます。 結果は次の図のとおりです。 彼は目を楽しませていませんが、何もありません。 そうすれば、Photoshopで不要なものをすべてカットすることができます。

いいですね。 しかし、これは広告投稿ではないため、重要な欠点を無視することはできません。 曲線が十分に滑らかで、ホイールが小さい場合、上記のすべてが機能します。 ホイールのサイズが曲線自体に匹敵する場合、上記の結論はもはや有効ではありません。 疑わしいノッチがグラフに表示されます。アルゴリズムに従って計算すると、一部の場所のホイールが1つの点でのみ外部曲線に接触し、その隣接点が突き出ていることがわかります。 もちろん、これは物理的な肺活量計では機能しませんが、現代の科学はまだそれを修正する方法を知りません。 誰かアイデアがあれば、投げてください。
そして最後に、プログラムのテキストであるアルゴリズムの厳しい発言よりも花の散文を好む人のために。 Asymptoteで書かれており、優れたコンピューターグラフィックスプログラミングツールです。
// , path base = scale(3,2)*unitcircle; // - ; , //path base = unitcircle; // - // path base = (-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle; // // (0 - , -1 - , +1 - ) real p = 0.7; import graph; size(600, 600); // //xaxis(ticks=Ticks); //yaxis(ticks=Ticks); // int m = 9; // int n = 29; // , real r = arclength(base)*m/2/pi/n; real hole = r*p; draw(base); //////////////////////////////////////////////// // , phase - real revolution(real phase) { pair prev = (500,500); real arclen = 0; real beta; real gamma; for (real alpha = 0; alpha<=2pi; alpha=alpha+0.005) { // real[][] isect = intersections(base, (0,0)--(500*cos(alpha), 500*sin(alpha))); pair pt = point(base, isect[0][0]); if (prev==(500,500)) { gamma = 0; } else { // arclen += length(pt-prev); // , pair deriv = pt - prev; // real g = atan2(deriv.y, deriv.x); // gamma = g - pi/2; } beta = gamma - arclen/r + phase; // pair local = hole*( cos(beta), sin(beta) ); // pair center = pt - r*( cos(gamma), sin(gamma) ); pair spiro = center + local; draw(center, green); draw(spiro, blue); // - prev = pt; } return beta; } //////////////////////////////////// // - real[][] isect = intersections(base, (0,0)--(100, 0)); pair first_point = point(base,isect[0][0]); draw(shift(first_point.xr,0)*scale(r)*unitcircle, yellow); // , real phase = 0; for (int rev=0; rev<m; rev=rev+1) { phase = revolution(phase); }