
場合によっては、数値シーケンスまたはバイナリデータを扱う場合、それらを「感じ」、それらがどのように配置されているか、圧縮されているか、暗号化されているか、どれだけ高品質であるかを理解したいことがあります。 擬似乱数ジェネレータについて話している場合、擬似乱数ジェネレータがどのように擬似乱数であるかを知りたいと思います。
実際、ここで考えられることは、まあ...期待、カウント分散、またはどのヒストグラムを構築するか...
次に、数値シーケンスから一種の指紋を取得できる方法を検討します。
- 多くの整数を生成できる整数のジェネレーターがあるとします(この場合は10,000,000)。
- 印刷のサイズを選択します。これを「ロール」し、Sz = 1024にします。
- サイズSzの整数の2次元正方行列のメモリを選択してゼロにします:ヒスト[Sz] [Sz]
- ジェネレータから数値を減算し、それらのそれぞれに対して(Val)サイクルを整理します
for (size_t ix = 1; ix <= Sz; ix++) { size_t histix = Val % ix; Hists[ix-1][histix] ++; }
- 十分な数の生成された値を実行した後、選択された範囲内のすべての数値で除算した残基の2次元ヒストグラムが得られます。 このヒストグラムは、ジェネレーターによって値が生成される順序に依存しないことに注意してください。 一方、値自体ではなくヒストグラムをフィードすることもできますが、たとえば、前のものとの違いは、順序が部分的に考慮されます
- 次に、結果のヒストグラムを見やすい形式で表示し( gnuplotは「 pm3dマップ 」モードで使用されます)、開いた画像を楽しみます。 出力がHists [ix] [[iy]から値を取得するのではなく、ヒットの確率を調整することに注意してください(Hists [ix] [iy] *(ix + 1)/ Sz)
それでは始めましょう。 そして、標準のC-shny randジェネレーターから始めます。

ヒストグラムは三角形で平坦であることが判明したと予想されますが、...およびこれらの奇妙なストライプは何ですか?
さらに詳しく考えてみましょう。
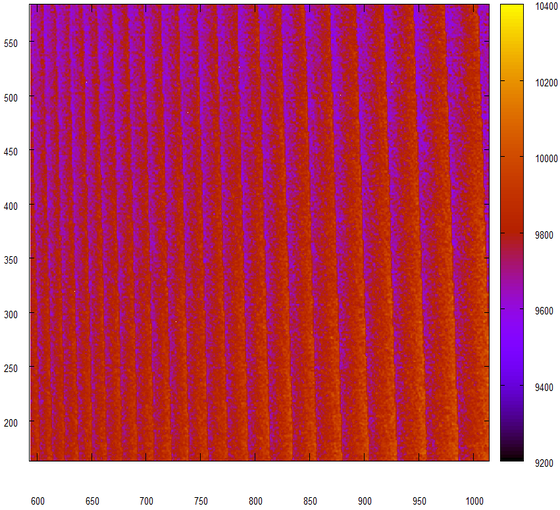
このジェネレータはあまり乱数を生成しないようです。 さて、私はrand()を乱数発生器として使用することは「悪い人の確実な兆候」(C)であると常に疑っていました。
おそらく、「正しい」乱数ジェネレーターを調べる必要があります。 そのため、ユーリ・タカチョフから何らかの形で提供されたものを使用します。
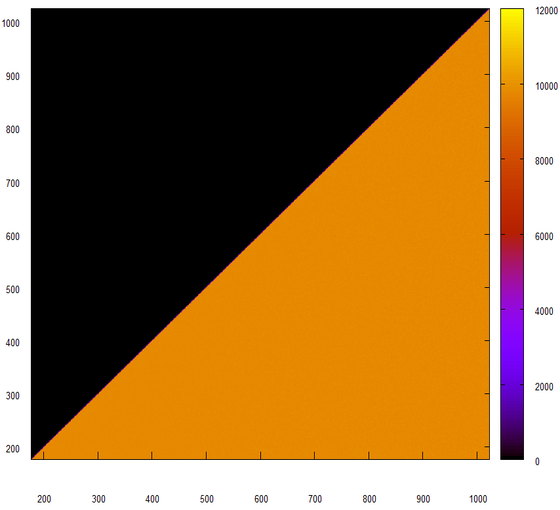
一見、それはよさそうだ。 このヒストグラムを見てみましょう。

はい、これはまさに乱数ジェネレーターから得られるものです。 データを少し移動してみましょう。下位24ビットのみを考慮します。
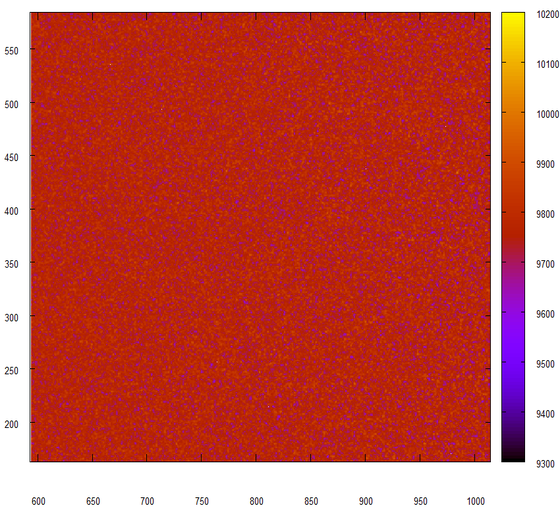
何も変わっていませんが、まさにそれが私たちが見たかったものです。 別の実験、今回は素晴らしいジェネレーターによって発行された2つの連続した数字の24ビットの断片を接着します。
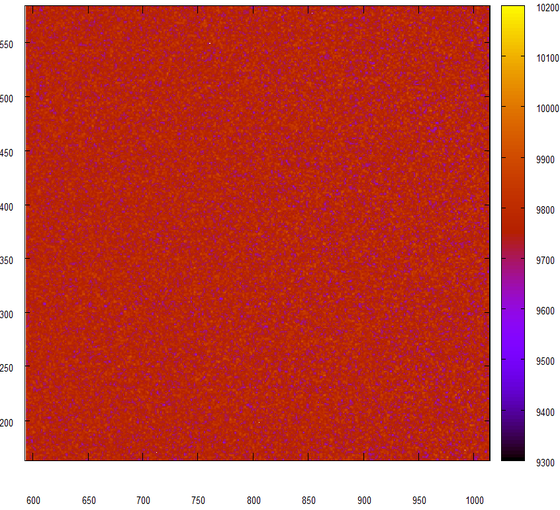
そして再び、違いはありません! 素晴らしい!
最後の試み、今回は24ビットのピースを接着するのではなく、それらを乗算します。
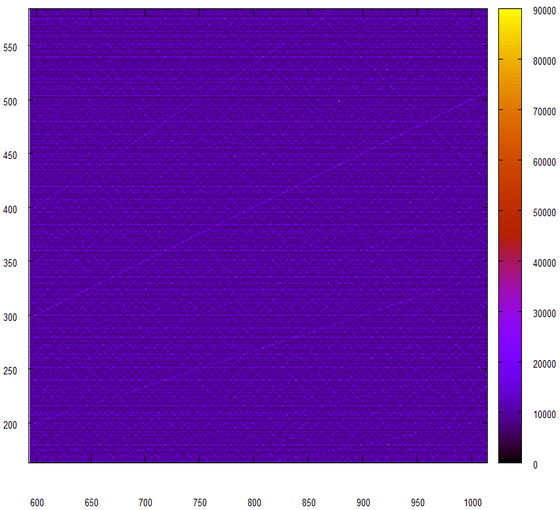
バム! そして、彼の擬似腸が私たちの乱数ジェネレータから抜け出したように感じます。
同じですが、スケールは異なります:
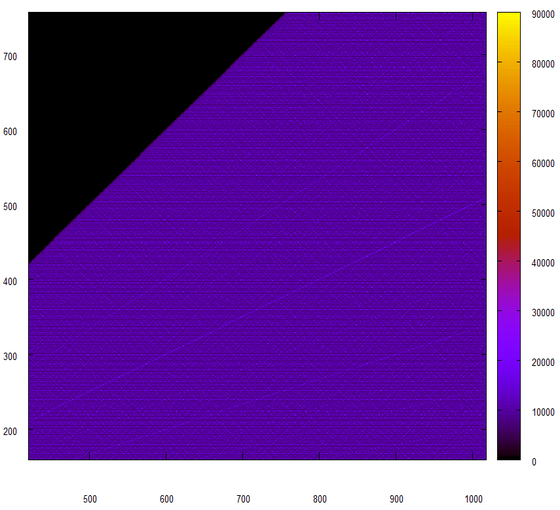
ああ、「ピーター・イワノビッチに言った」(C)。
一息ついて、何が起こったのかを理解するために時間を稼ぐために、異なる種類のデータがどのように見えるかを見てみましょう。

これらは、データベースイメージファイルから差し引かれた最初の1,000万個の64ビット整数です。
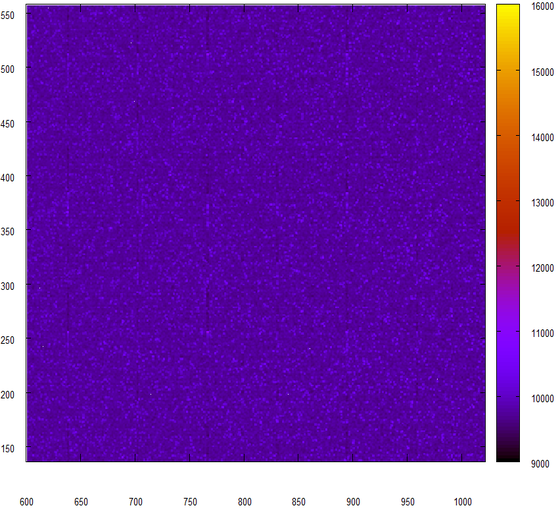
次に、同じ方法で取得したデータを示します。ソースはzipファイルです。
ランダムなデータのように見えますが、縦線はすべてを台無しにします。
そのため、注意深い読者はファイルからデータを読み取ることに戸惑いましたが、著者は非常にランダムなシーケンスの動作を確認することにしました。 F(n)= F(n-1)+ 1から始めます。 0、1、2、3 ...
シーケンス自体のヒストグラムも見ていません。これは三角形で完全にフラットであり、直感的で説明が簡単です。 実際、このメソッドには順序がないため、このようなシーケンスは、範囲全体を等しくスイープする理想的な乱数ジェネレーターのように動作します。
ただし、2つの数値(それぞれ0〜4000)の積の分布は次のようになります。
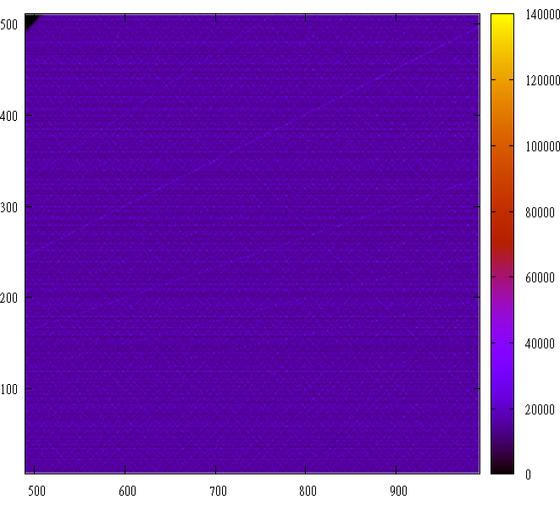
とても身近な絵ですね。 実際、2つの数値の積の参照ヒストグラムサンプルが表示されます。
一か所で、 製品と部門の残りの部分が一緒になりました。
かなり気取らない方法で、私たちは床の下から数字の魔法を引き出しました。
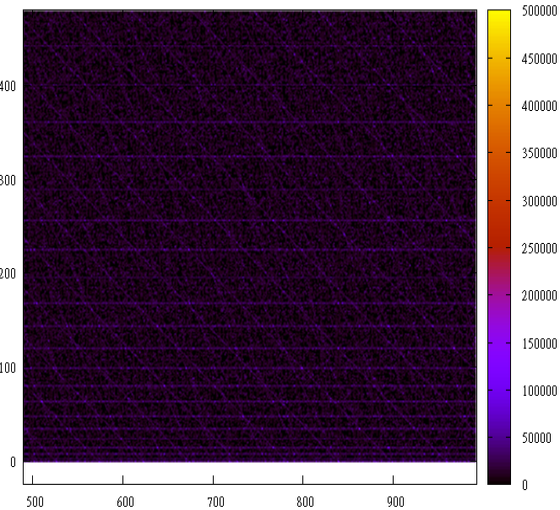
そして、これがシーケンスF(n)= n * nの動作です。 0、1、4、9 ...

そして、ここでF(n)= 2 * n *(2 * n + 1)つまり 0 * 1、2 * 3、4 * 5 ...
そして最後に、著者は最初の1,000万個の素数の分布を示すことに抵抗できませんでした。

そして彼らの「キャスト」-最初の1000万の難しい数字(ちょうど美しい)。
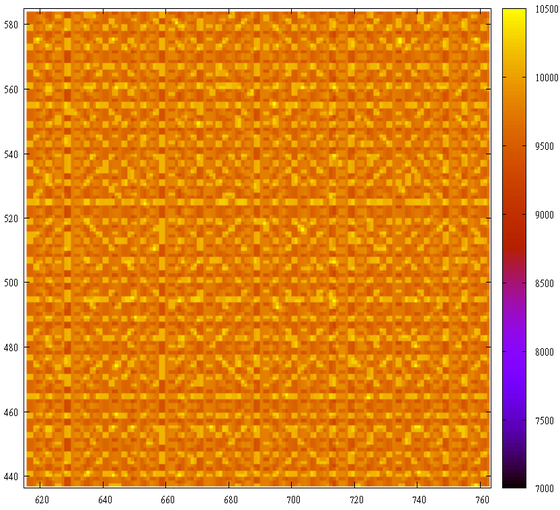
まあ、警戒してください、そして、「常に、いや、決して」(C)はシーケンスを掛けません:)。
PS。 著者は、subjの活発な議論に対してAlexander Artyushinに特別な感謝を表明します。