
この記事は翻訳です。 ここから始めてください 。
出所
プログラム内:
1)ワイヤは空中に垂れ下がっていますが、電流/電圧源に短絡が見られます。
2)ワイヤの一方の端での振幅は0ボルトで、もう一方の端では1ボルトです。 これはどのように可能ですか?
3)適切に選択されたケーブルを使用して、75オームの信号ソースと300オームの負荷を一致させます。
定在波と共鳴
伝送ラインの抵抗と負荷の間に不一致があるときはいつでも、反射が発生します。 入射信号に1つの周波数がある場合、この信号は反射波に重畳され、定在波が表示されます。
図は、三角形の入射波がラインの開放端からどのようにミラーリングされるかを示しています。 簡単にするために、この例の伝送ラインは、ワイヤのペアとしてではなく、1本の太線として示されています。 入射波は左から右に進み、反射波は右から左に進みます。
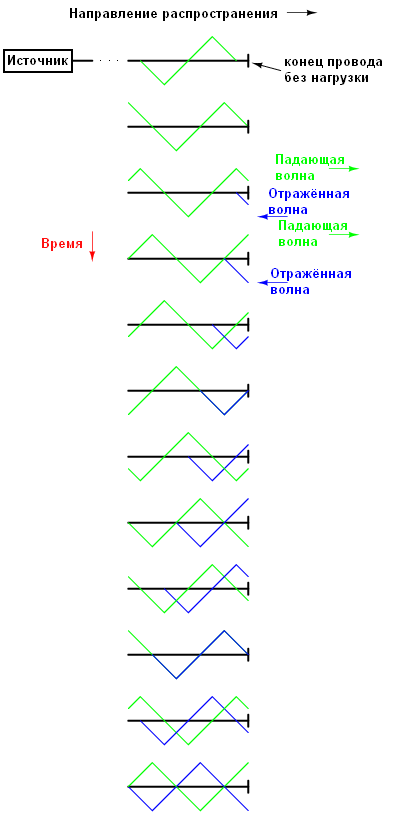
これらの2つの信号を追加すると、線の全長に沿って3番目の定常信号が作成されることがわかります。下図の赤い線は、入射波と反射波の合計です。

この3番目の波は、入射波と反射波の合計です。 入射波や反射波のようにケーブルに沿って移動することはありません。 入射波と反射波が常に互いに打ち消し合う線に沿った点に注意してください。これらの点は位置を変えません。

定在波は、物理的な世界でも一般的です。 ロープを片側で縛って考えてみましょう:

ノット(振動のないポイント)と波腹(最大の振動のポイント)は、ロープの全長に沿って変化しません。 また、弦楽器は定在波を作成し、その長さに沿って最大および最小の振動のノードがあります。 ロープ楽器と弦楽器の主な違いは、楽器がすでに正しい振動周波数に調整されていることです。

開いたパイプから吹く風も定在波を生成します。 この場合、チューブ内の空気分子は振動し、固体は振動しません。 定在波は、節点(最小振幅)または波腹(最大振幅)で終了できます。これは、チューブのもう一方の端が開いているか閉じているかによって異なります。
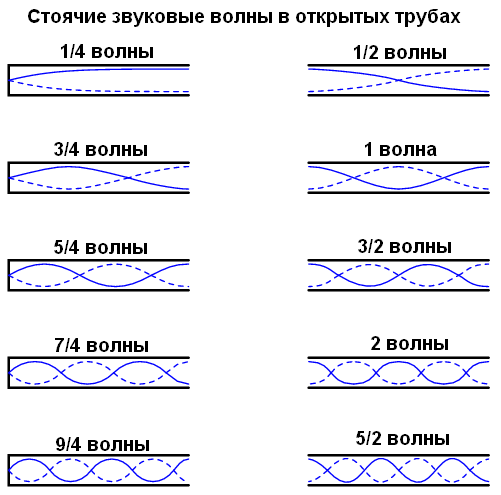
パイプの閉じた端は結び目を作成し、開いた端は波腹を作成します。 同様に、ストリングアンカーは結び目であり、自由端(ある場合)は波腹です。
パイプ内では、異なる周波数の定在波が発生する可能性があることに注意してください。 定在波をサポートするシステムには、いくつかの共振周波数があります。
より高い周波数は、基本周波数の倍数でなければなりません。

これらの高調波(倍音)の実際の周波数は、パイプの物理的なサイズと波の伝播速度(この場合、音の伝播速度)に依存します。
通信回線に定在波を作成することもできます。その周波数は、回線の終端での負荷の種類、伝搬速度、および物理的な長さに依存します。 送電線の共鳴は、パイプの弦や空気の共鳴よりも複雑です。これは、波の電圧と電流を考慮する必要があるためです。
伝送線路の共振は、コンピューターシミュレーションを使用すると理解しやすくなります。 開始するには、一致する75オームの回線を検討します。

SPICEを使用して回路をシミュレートし、T1ラインに対して75オーム(z0 = 75)の波動抵抗と1μsの伝搬遅延を示します。 これは、伝送ラインの物理的な長さ、つまり信号が伝搬するのにかかる時間を表す便利な方法です。 実際のケーブルRG-59B / Uの場合、長さは198メートルになります。 1μsは1 MHzの周波数に対応します。 ゼロからこの周波数までの周波数を選択して、システムが異なる周波数にどのように応答するかを示します。
SPICEモデルは次のとおりです。
| 送電線
v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 75 .ac lin 101 1m 1meg *「Nutmeg」プログラムを使用して分析をプロットする .end |
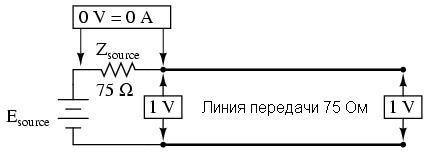
このシミュレーションを実行して、ソース抵抗(Zsource)での電圧降下のグラフを作成します-これは、電流インジケーターとラインの端での電圧グラフ(負荷での電圧)です。 電圧源は、vm(1)(ノード1と接地点0の間の電圧)が正確に1ボルトであるため、グラフに表示されます。 ポイント2と3の電圧は0.5ボルトです。 抵抗の両端の電圧-電流インジケータとして-は0.5ボルトになります。
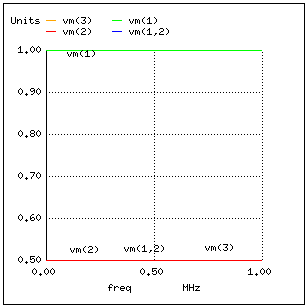
すべての抵抗が完全に一致するシステムでは、定在波は存在せず、ボード線図には共振がありません。
次に、抵抗を999MΩに変更して、オープン伝送ラインをシミュレートします。 1 MHzから1 MHzまでのいくつかの周波数で反射波を取得する必要があります。

| 送電線
v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 999meg .ac lin 101 1m 1meg *「Nutmeg」プログラムを使用して分析をプロットする .end |

ここで、ライン供給電圧vm(1)と負荷の電圧は同じレベル(1V)のままです。 その他の電圧降下は、周波数(1 MHz〜1 MHz)に依存します。 水平線に沿って5つの注目すべき周波数があります:0Hz、250kHz、500kHz、750kHz、1MHz。 回路のさまざまなポイントでの電圧と電流を考慮して、各ポイントを調べます。
•0Hz(実際には1MHz)はほぼ一定の電流信号であり、回路は1VDCが印加された場合と同じように動作します。 Zsource抵抗器でゼロ電圧降下が示されているため、電流は流れません。グラフはvm(1,2)であり、ソースの電圧はラインvm(2)の端の電圧に等しくなります(ポイント2とポイント0の間の電圧)。
•250 kHzでは、ポイント2でゼロ電圧、ソースからの最大電流、およびラインの終端での合計電圧が見られます。

これがどのようにできるのか疑問に思うかもしれません。 入力電圧がゼロの場合、ラインの開放端で全電圧を取得するにはどうすればよいですか? 答えは定在波のパラドックスにあります。 250 kHzでは、ラインの長さは波長のちょうど1/4です。 ラインの終端が開いているため、電流は流れませんが、電圧は流れます。 したがって、ワイヤの端には、電流のノード(電流はゼロ)と電圧のアンチノード(最大振幅)があります。

•500 kHzの周波数では、波のちょうど半分がラインに収まります。ここで、電流がゼロになり、電圧が再び最大振幅になる別のポイントが表示されます。

•750 kHzの周波数では、画像は250 kHzの周波数に似ています。ソースの電圧はゼロで、最大電流です。 ¾波はラインに収まります。その結果、ソースは伝送ラインへの接続点で短絡が発生しますが、ラインのもう一方の端に切れ目があります。

•周波数が1 MHzに達すると、1つの全波周期がラインに配置されます。 現時点では、ラインの開始時の電流と電圧の両方が、ラインの終了時の電流と電圧に等しくなっています。 また、ラインの終わりで電流がゼロ(抵抗が999MΩ)の場合、ラインの始めで電流もゼロになります。 ソースの電圧は負荷の電圧に等しくなります。 実際、ソースには開回路があります。
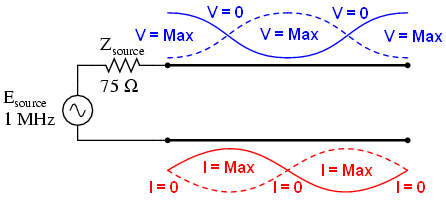
同様に、電流と電圧の節点と波腹は変化しますが、線の端の短絡は定在波を生成します:線の短絡端では電圧(節)はありませんが、最大電流(節)があります。 次に、SPICEシミュレーションと、すべての興味深い周波数(0Hz、250kHz、500kHz、750kHz、1MHz)で起こることの説明です。 短絡は、0μOhmの負荷抵抗によってモデル化されます。

| 送電線
v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 1u .ac lin 101 1m 1meg *「Nutmeg」プログラムを使用して分析をプロットする .end |





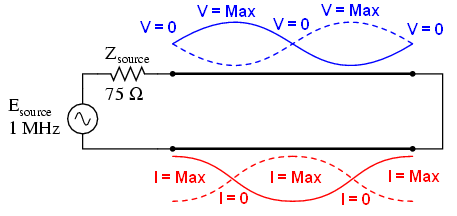
両方の例(開いた線と短絡した線)では、すべてのエネルギーが反映されます。 入射波の100%がラインの終わりに到達し、反射してソースに戻ります。 ただし、伝送ラインにある程度の抵抗がかかっている場合、ラインに沿った電圧と電流の最大値と最小値に差が生じます。
75ではなく100オームの抵抗をラインにロードしたと仮定します。
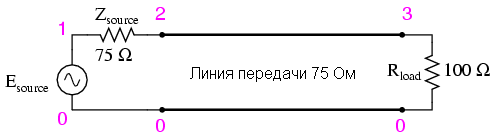
この場合のモデルを作成しましょう:
| 送電線
v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 100 .ac lin 101 1m 1meg *「Nutmeg」プログラムを使用して分析をプロットする .end |

グラフの代わりにテキスト値の出力を使用して別のSPICE分析を実行すると、興味深い周波数はすべて同じままであることがわかります(DC、250 kHz、500 kHz、750 kHz、および1 MHz)。
| 送電線
v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 100 .ac lin 5 1m 1meg .print ac v(1,2)v(1)v(2)v(3) .end |
| 頻度 | v(1,2) | v(1) | v(2) | v(3) |
| 1.000E-03 | 4.286E-01 | 1.000E + 00 | 5.714E-01 | 5.714E-01 |
| 2.500E + 05 | 5.714E-01 | 1.000E + 00 | 4.286E-01 | 5.714E-01 |
| 5.000E + 05 | 4.286E-01 | 1.000E + 00 | 5.714E-01 | 5.714E-01 |
| 7.500E + 05 | 5.714E-01 | 1.000E + 00 | 4.286E-01 | 5.714E-01 |
| 1.000E + 06 | 4.286E-01 | 1.000E + 00 | 5.714E-01 | 5.714E-01 |
すべての周波数で、ポイント1のソースの電圧は予想どおり1ボルトです。 負荷の電圧も一定のままですが、振幅は小さくなっています(0.5714ボルト)。 ただし、線間電圧(ポイント2、グラフv(2))および電流(グラフv(1,2))は、ソースからの電流が周波数によって変化することを示しています。





基本周波数の奇数次高調波(250 kHzおよび750 kHz)では、ラインの始点と終点で異なる電圧レベルが見られます。これらの周波数では、定在波がラインの片側にノードを作成し、反対側に腹を作成するためです。 開いた線や短絡した線とは異なり、最大値は元の信号のゼロまたは100%には達しません。 しかし、まだ最小電圧と最大電圧のポイントがあります。 電流についても同じことが言えます。 ラインの負荷抵抗がラインの波抵抗に対応していない場合、ノードとアンチノードに対応する伝送ラインのいくつかの固定ポイントに最大電流と最小電流のポイントがあります。
定在波のレベルを表す1つの方法は、電圧または電流の最大振幅(腹のポイントでの)と最小振幅の比です。 この比率は、SWR-定在波係数と呼ばれます。 回線にオープンまたはショート回路がある場合、最小振幅はゼロになるため、SWRは無限大に等しくなります。 この例では、負荷100オームSWRの75オームラインは1.333です。250または750 kHz(0.5714 V)での最大ライン電圧を最小ライン電圧(0.4286 V)で割ったものです。
SWRは、大きな値を小さな値で除算することにより、ラインの負荷抵抗と波動インピーダンスを知ることでも計算できます。 この例では、100Ω/75Ω= 1.333です。

負荷が完全に一致するラインのSWRは1になります。これは、反射波が負荷に到達していないエネルギーであるためだけでなく、高電圧および高電流のために理想的であると考えられます。大電流は導体を損傷します。
また、SWRの低い回線はアンテナとして機能します。 これは望ましくありません。このようなアンテナは近くの配線に干渉する可能性があります。 興味深いことに、アンテナはオープン伝送ラインであり、1に近いSWRで動作します。可能な限り、これはすべてのエネルギーが放射されることを意味します。
次の写真は、無線送信機の通信回線の接続ポイントを示しています。 セラミック絶縁体を備えた大きな銅パイプは、50オームの波動インピーダンスを備えた剛性の同軸線です。

50オームの波動インピーダンスを持つ柔軟な同軸ケーブル。 白いプラスチックパイプがパイプ内のガスを接続します。これらは湿気から保護するために密閉されています。 ラインを接続するためのフラットワイヤに注意してください。 なぜ丸くないのか これは表皮効果によるもので、高周波数では大きな断面積が役に立たなくなります。
多くの通信回線と同様に、低SWRで動作します。 次のセクションで説明するように、通信回線での定在波の現象は、有害な機能であるインピーダンス変換に使用できるため、必ずしも有害ではありません。
インピーダンス変換
短絡線または開放線の共振点での定在波は、異常な効果を生み出す可能性があります。 線の長さが½波長(およびそれ以上の倍数)の場合、ソースは負荷をそのまま認識します。 次の図にこれを示します。


どちらの場合も、電圧の腹と電流の節は線の端にあります。 ラインは負荷を模倣します-無限の抵抗、ソースは破損を確認します。
ライン上に短絡がある場合も同様です。ソースの接続ポイントでは、電圧が最小で電流が最大になります。


ただし、ラインの長さが波長の4分の1に等しい場合、ソースはラインの終端で短絡が発生し、破線が短絡として表示されます。
回線が開いており、ソースに短絡が見られます。


行が閉じられ、ソースにブレークが表示されます。


これらの周波数では、伝送ラインは抵抗トランスのように動作し、無限抵抗をゼロに、またはその逆に変換します。 これは、4分の1の波がラインに収まり、はるかに大きい(3 / 4、5 / 4、7 / 4、9 / 4 ...)共振点でのみ発生しますが、周波数が既知で変化しない場合は、この現象をマッチングに使用できます互いに異なる波動インピーダンス。
たとえば、負荷が100Ωの75Ω伝送ラインを考えてみましょう。 SPICEの数値シミュレーションから、ソースにどのような抵抗があるかを判断します。




簡単な方程式は、奇数高調波での一貫性のないラインのラインインピーダンス(Z0)、負荷インピーダンス(Zload)、および入力インピーダンス(Zinput)を関連付けます。

300Ωの負荷と75Ωのソースを整合させる必要がある場合の実用的な例を考えてみましょう。 必要なのは、50 MHzで1/4波長の正しいラインインピーダンスと長さを計算することだけです。
まず、ライン抵抗を計算します。 Z0 = Sqrt(75 * 300)=150Ω。
次に、線の長さを計算する必要があります。 0.85の短縮係数、30万km / sの光速度、255万km / sの信号速度を想定します。 この速度を信号周波数で除算し、5.1メートルの波長を取得します。 四分の一波長が必要です-それは1,275mです。
SPICE分析の図は次のとおりです。

信号遅延によってラインの長さを示すことができます。 50 MHzの周波数では、周期は20 nsになります。 四分の一波長の遅延時間は5nsです。
| 送電線
v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 150 td = 5n rload 3 0 300 .ac lin 1 50meg 50meg .print ac v(1,2)v(1)v(2)v(3) .end |
| 頻度 | v(1,2) | v(1) | v(2) | v(3) |
| 5.000E + 07 | 5.000E-01 | 1.000E + 00 | 5.000E-01 | 1.000E + 00 |
ポイント1-2で50 MHzの周波数で、正確に半分の電圧降下-0.5 Vで、2-0回路の通信ラインで電圧の後半が降下します。 これは、ソースが負荷で75Ωを認識することを意味します。 ただし、負荷は半分ではなく1ボルト(電圧v(3))を受け取ります。 75Ωの抵抗、0.5 Vまたは3.333 mWの低下-1 Vの電圧で300オームの負荷の場合と同じです。 最大電力定理(ヤコビ定理)に従って、最大可能電力は負荷で消費されます。 150Ωの波動インピーダンスと300Ωの負荷を持つ1/4波長伝送ラインは、75Ω負荷のように動作します。
もちろん、これはすべて50 MHzおよび奇数の高調波でのみ動作します。 他の周波数の場合、伝送ラインを延長または短縮する必要があります。
奇妙なことに、同じ長さのラインは300Ωのソースと75Ωの負荷に一致します。 これは、インピーダンス変換の現象が、2つの巻線を持つトランスの動作原理と根本的に異なることを示しています。
| 送電線
v1 1 0 ac 1 sin rsource 1 2 300 t1 2 0 3 0 z0 = 150 td = 5n rload 3 0 75 .ac lin 1 50meg 50meg .print ac v(1,2)v(1)v(2)v(3) .end |
| 頻度 | v(1,2) | v(1) | v(2) | v(3) |
| 5.000E + 07 | 5.000E-01 | 1.000E + 00 | 5.000E-01 | 2.500E-01 |
この場合、0.5V、つまり833μWがソースの内部抵抗に落ちます。 負荷では、同じ833mWの0.25Vがあります。
この方法は、周波数が既知で不変であることが多いため、無線送信機の伝送ラインとアンテナのマッチングによく使用されます。 インピーダンス変換器の最小長は、1/4波長に相当します。
