初等衛星フライトシミュレーター

私は最近、中心体の周りに衛星飛行シミュレータを書くことにしました。 すぐに、衛星の質量が中心体の質量と比較して無視できるほど小さいことを予約してください。





実際、仕事の最初の部分は数学の研究でした。 それは非常に簡単でした。基本的な運動方程式が使用されました。

/* t -   G -  (  ) msun -    (  ) */ var r2=(xsun-xc)*(xsun-xc)+(ysun-yc)*(ysun-yc); //  - var gs=G*msun/r2; // ,   //      var ivx=(t*t*gs/2)*(xsun-xc)/Math.sqrt(r2); var ivy=(t*t*gs/2)*(ysun-yc)/Math.sqrt(r2); //     vx+=ivx/t; vy+=ivy/t; var V=Math.sqrt(vx*vx+vy*vy) //   /*  */ xc+=vx*t; yc+=vy*t;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実際、これで数学的な部分は終わりました。

インターフェース

アイデアによると、ユーザー自身が開始点を選択し、自分自身が初期速度を報告することが計画されていました。

2つのイベントリスナーを介してJSに実装されます。

 var xc,yc,xc2,yc2,intervalID,vx,vy; /*   */ cnv.addEventListener('mousedown',function (event) { /*     */ xc=event.offsetX; yc=event.offsetY; /*      */ clearInterval(intervalID) }, false) /*      ,       */ cnv.addEventListener('mouseup',function (event) { /*      */ clearInterval(intervalID) /*    */ xc2=event.offsetX; yc2=event.offsetY; /*    */ vx=(-xc+xc2)*0.4 /*  */ vy=(-yc+yc2)*0.4 intervalID=setInterval(dodo,70); }, false)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

テスト中

最初のテストは天文学者として私にとって非常に興味深いものでした）

軌道が非常に楕円形の場合、次のように歳差運動します。



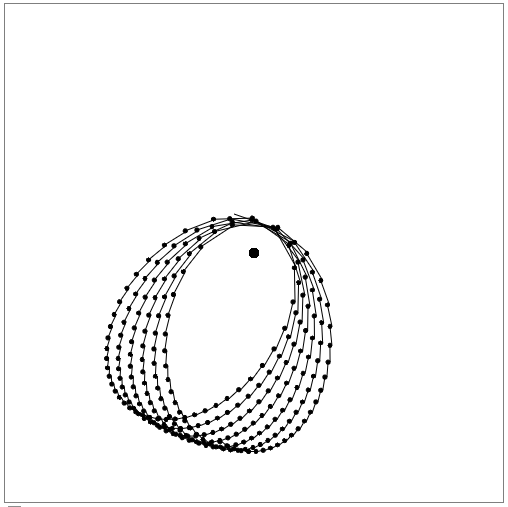
一方で、そのような現象を見るのは良いことでしたが、他方では、ここでのポイントは歳差運動ではなく、時としてそのような軌道があったために位置を計算することの不正確さであることに気付きました：



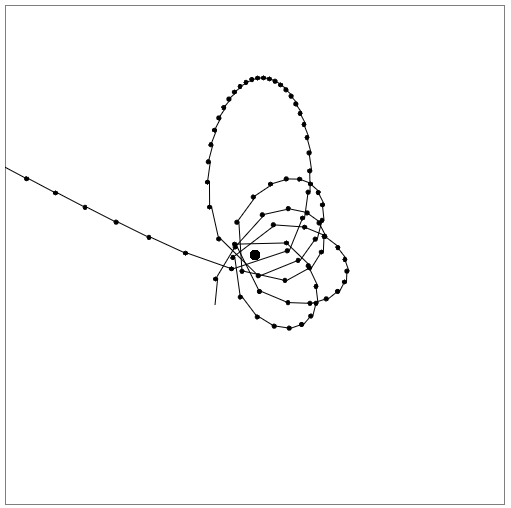
実際、問題は単純であることが判明しました。理想的には、アニメーションは時間で区別する必要があります。つまり、速度とその方向にあまり変化のないような小さな時間ステップに分割する必要があります。 そして、一定の時間ステップを設定し、このステップで遠日点の衛星の位置を計算するのに十分であれば、過熱状態では数倍小さくなります。 このため、位置を計算するためにフローティングステップが取られましたが、描画ステップは一定のままでした。

実装：

 var i=0; do{ var r2=(xsun-xc)*(xsun-xc)+(ysun-yc)*(ysun-yc); var gs=G*msun/r2; var ivx=(t*t*gs/2)*(xsun-xc)/Math.sqrt(r2); var ivy=(t*t*gs/2)*(ysun-yc)/Math.sqrt(r2); vx+=ivx/t; vy+=ivy/t; var V=Math.sqrt(vx*vx+vy*vy) xc+=vx*t; yc+=vy*t; i++ }while(i<=1/t)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

デバッグ

改良のために、衛星の半径ベクトルを作成しました。これは、衛星が画像の外側を飛んだときの位置を理解するのに役立ちます。

 ctx.moveTo(xc,yc) ctx.lineTo(xsun,ysun) ctx.stroke()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてがここにあります： http : //astrokot.ru/planetarium/vectors.html