ほぼ科学的な書籍やカオスに関するWebページは、ほぼ19世紀から知られている同じモデルを操作します。フラクタル、乱流、ロジスティックマッピング...
一方、過去10年間で、動的なカオスが(自己組織化とともに)であることが明らかになりました
私たちの意識の起源と仕事を含む、宇宙を理解するための鍵 。
このテーマに関する深刻なモノグラフには、高度なトレーニングと数学的文化が必要です。
(誰もが持っている、私はお勧めします:
A.B. カトック、B。ハッセルブラット「動的システムの現代理論の紹介」)。
もちろん、バランスの取れたアプローチの例があります。
- G.M. ザスラヴスキー、R.M。 Sagdeev「非線形物理学入門」
- S.P. クズネツォフ「ダイナミックカオス」
- A.リヒテンベルク、M。リーバーマン「正規および確率論的ダイナミクス」
コンテンツサイトもあります。
サラトフの非線形ダイナミクスのグループ
神秘的なサイト
カオスの階層、確率論の基準に関するかなり最近の興味深い出版物です。
そこの数学は恐ろしく見えます。 集合論の十分な知識。
ここで、同様のトピックをカバーしたいと思います。ランダム性の基準の1つを分析し、
自己分析のための家庭実験を提供します。
膨大な数の基準とランダム性のテストがあります。
上記の記事は説得力を持って示しています。「カオスかどうか?」という質問に対するバイナリの答えはありません。
スクリーンをしっかりとシェーディングするリサージュの人物から、高次元のハイパーカオスまで、
「正直な」骨を投げることと見分けがつかない-これらのシステムはすべて、異なる方法を使用して評価できます。
(相関、スペクトル、混合...)、カオスの階層を取得します。 より多くのアプローチ-カオスのより多くの顔...
たとえば、Habrとの知り合いはこの記事から始まりました
時系列を表示する1つの方法について。 彼がかつて思いついた似たようなもの。 これがそんなに強力な視覚化方法になるとは思っていませんでした。
それでも、人間の意識は確実性、普遍性を求めています。
まあ、明確な正弦波から乱流まで、巨大な塔になりましょう...
しかし、普遍的な「カオスメーター」を見つけて、さらに結果をパーセントで表示することは非常に興味深いです(時には非常に重要です)。 もちろん、同様の方法が知られています。 相関の減衰の程度、リアプノフ指数には特定の数値があります。
乱数、sinとcosの複雑な組み合わせ、および黒点の数の自己相関関数:
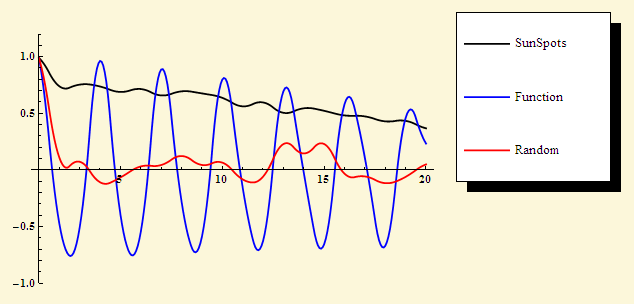
しかし、それはそれほど単純ではありません。 一部の方法では、データ系列を繰り返し複数回取得する必要がありますが 、これは常に可能とは限りません。 これは、「軌跡の発散」の概念を使用するすべての方法に適用されます。
他の人には、現象の分析モデルが必要です。 シリーズのそのようなモデルを構築するため
「プライム」と呼ばれる数字、あなたは不注意に100万を得ることができます...
最下位に到達したいという欲求は、ドナルド・クヌースの壮大な教科書にやがて導いた
「プログラミングの芸術。」 第2巻には、セクション3.5「 ランダムシーケンスとは 」があります。
そこで、Knutは∞分布の概念を解析し、次のように記述します。
「著者は、この定義が偶然の合理的な哲学的要件をすべて満たしていると主張しているため、このセクションで提起された主な質問に答えています」
これは1966年に言われましたが、今でも「クヌート法」が最も基本的です(IMHO)。
文字通り高校生が数学を学べるので、この章を読み直してください。
ここでは、実際に使いやすいある種の適応を紹介します。
1. すべてのデータは、ゼロと1のシーケンスとして表すことができます。
それらをこのフォームに正しく持ち込む方法は別の問題です。 原則として、分布分析は実数と整数の両方、さらにはシンボルに対して実行できます。 ... 01011000111で作業します...
2.「痛点」は記録の長さです 。 5つのゼロと1の任意のシリーズをランダムまたは確定と見なすことができますか?! そして、100から?..これは、「ヒープかどうか?」というよく知られたパラドックスにつながります。
KnutはEのこの質問を解析します。
3.最後に、分析を取り上げます。 レコード内のゼロと1の数を数えます。
長さNのシーケンスに、n個のゼロとNn個の1があると仮定します。 それらの相対量r1 = n / N、
r2 = 1-r1はランダム性の最初の特性です。 それらが非常に異なる場合、データは明らかにランダムではありません。
「どれだけ強い?」というもう一つの「つるつるした」質問です。 明確な答えはありませんが、 statメソッドを使用できます。
ゼロと1の端数がほぼ等しい場合、 明確なことは言えません。
確かに、厳密に周期的なシリーズ1010101010101では...それらも同等です!
4. レコードをペアに分割します 。 さまざまな方法で可能です。
{abcdef ...}-> {{ab}、{cd}、{ef}、...}または{abcdef ...}-> {{ab}、{bc}、{cd}、{de} 、...}
正直なところ、私はどちらの方法がより正しいかを研究していません。 しかし、オーバーラップ法はより多くのペアを提供します。 それを使用します。
m個の異なるオブジェクトから、m ^ 2個のペアを形成できます。 私たちの場合、これらは{00}、{01}、{10}、{11}です。
相対量を計算します。 分散度と分散度のさまざまな統計的基準を、取得した4つの数値のセットに適用できます。
意味は1つだけです。 ペアが複数ある場合、パターンがあります 。 たとえば、行101010101には、00と11はまったくありません。均等に分散されたペアは、混乱の可能性を示していますが、以前と同じ注意事項があります。
だから「考えられたかもしれない」。
5.さらなるステップは理解できると思います。 トリプル(2 ^ 3 = 8になります)、フォースなどを形成します。
分布を確認します。
Knutによると、すべてのセットに均等に分散されたシーケンスは、純粋な真のカオスです。
実際には、ld(N)(ldは2を底とする対数)以下のセットを分析するのが理にかなっています。
それらがすべて均等に分布している場合-データ系列は、その長さが判断できる限り混chaとしている。
異なるセットのヒストグラムの散布の特徴は、現象の性質に関する貴重な情報を提供できます。
数字Piの数字のヒストグラム、素数を13で割った残り(なぜですか?これは別の問題です)、および2012年のモスクワの風向(明確にするために、データは10進数ではなく10進数でした)
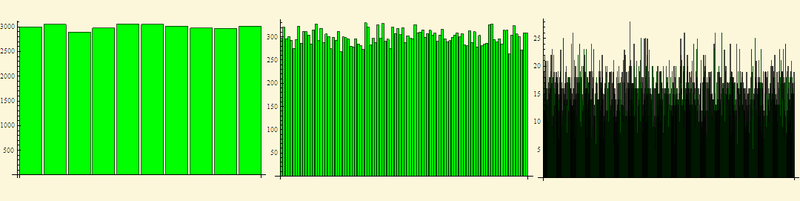
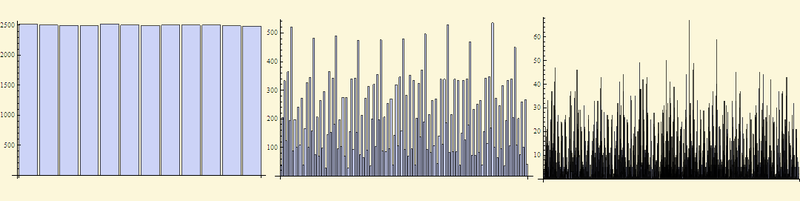
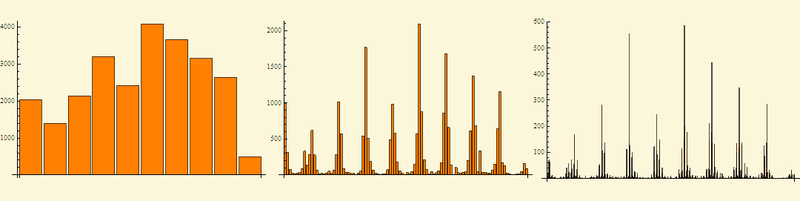
そして今、約束された家の実験 (M.シュローダー「フラクタル、カオス、べき法則」に述べられている)。
メモ帳を開き、「0」および「1」キーボードに人差し指を置きます。
タスクは、ゼロと1のランダムシーケンスを埋めることです。
この記事を読んだ人は、ランダム性の度合いをどのように評価するかをすでに知っています。
しかし、私を信じて、これはさらなる結論にはほとんど無関係です。 経験の純粋さのために、もちろん、
「知らない」人に提供してください。
もっとデータがあるはずです。 だから目を閉じて、カオス・インサイドに目を向ける方がいい。
暗いアンビエントノイズのような非リズミカルな音楽を入れることができます...
そのため、電報は受信されました。 最も尊敬されているハブロビテ人は自分のプログラムを書くことができると思います
Knut分析用。 Mathematicaでは、3行かかります。
おそらくRには適切なライブラリがありますが、確かではありません。
GeoGebra (Wolfram Mathematicaの後のお気に入りのおもちゃ)でアプレットを使用することをお勧めします 。
新しいJavaプラグインが必要です。 ページをリロードする必要があるかもしれません。
ボタンを使用して、3つのプリセットの分析データを確認します。
作業をコピーし、アプレットの入力行にtext = ""と入力して、データを貼り付けます
引用符の間(テキスト= "100110101"); Enterキーを押します。 0.1以外の文字は無視されます。
それで、私たちは何を見ますか?
ゼロと1の数が著しく異なる場合、この
おそらく、ホットキーを無視して、常にマウスを使用しています。 またはたくさん撃って......
通常、それらはほぼ均等に分割されます。 そして今、ペアは驚くべき結果をもたらします。
「実験的」{01}と{10}の大半は、{00}と{11}のほぼ2倍です。
トリプルとフォーがさらに悪化します。 ある知り合いがなんとか1000文字以上を埋めること
単一の{0000}と{1111}なし!
ホモサピエンスの場合、「カオス」の概念は、 交互 、一定の切り替えに着実に関連付けられています。
さらに、このつながりは意識的なレベルだけではありません。 上記のすべてを知って、もう一度乱数を蓄積してみてください。 最良の場合、ペアのコンテンツを「レベルアウト」することが可能です。
一方、真のカオスは秩序の欠如だけではありません。
これらはすべて「1本のボトル」で可能な注文と構造のタイプです。
もちろん、私たちの意識と動的なカオスとの関係について言及したとき、私はその確率論を意味しませんでした
すべてのレベルで。 あなたは実験のアイデアを発展させることができます-タブレットに落書きを描き、ランダムな音を立てます...分析は、単純な「シャッフル」の傾向を示します。
カオスを真似することはできません。 それでも「彼はどこか近くにいる」。
これについては、次の投稿で詳しく説明します。