cな発見的方法、想像力、半リットルの助けを借りて、特定の解決策を見つけることができますが、原則として、この解決策の最小性または存在しないことを証明する適切なツールはありません(もちろん、後者は解決策が見つからなかった場合を指します) 。 これは悲しく不公平です。 そして、空白のノートブックを手に入れて、特定の1つのタスクの規模で正義を取り戻すことに決めました。平面図を2つの等しい(一致する)パーツに分割します。 この記事のシリーズの一部として(ちなみに、そのうちの3つがあります)、私たちは以下に示すこの面白いポリゴンを見て、それが2つの等しい数字にカットできるかどうかを公平に把握しようとします。
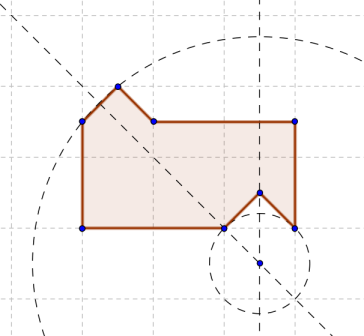
はじめに
まず、学校の幾何学コースを更新して、等しい数字とは何かを思い出しましょう。 Yandexは親切にプロンプトを表示します:
平面上の2つの図形は、1対1で1つの図形を別の図形に変換する動きがある場合、等しいと呼ばれます。
次に、この動きについてウィキペディアに質問します。 彼女は最初に、運動は点間の距離を保持する平面の変換であると教えてくれます。 第二に、飛行機の動きの分類さえあります。 それらはすべて、次の3つのタイプのいずれかに属します。
いくつかの表記法を紹介します。 カットされた図形を図形Aと、カットできる2つの仮想の等しい図形と呼びます。それぞれBとCと呼びます。 図形のAで占められていない平面の部分を領域Dと呼びます。写真の特定のポリゴンがカット図形と見なされる場合、A 0と呼びます 。
したがって、図形Aを2つの等しい部分BとCに切断できる場合、BをCに変換する動きがあります。この動きは、平行移動、回転、または移動対称のいずれかです(この時点から、私は規定しませんそのミラー対称性も移動していると見なされます)。 この単純な、そして明らかな根拠に基づいて、私たちの決定が構築されます。 このパートでは、最も単純なケースであるパラレル転送について検討します。 回転対称性とスライド対称性は、それぞれ2番目と3番目の部分に分類されます。
ケース1:並列転送
並列転送は、単一のパラメーター-シフトが発生するベクトルによって指定されます。 さらにいくつかの用語を紹介します。 シフトベクトルに平行で、図形Aの少なくとも1つの点を含む線を割線と呼びます。 割線と図Aの交点をセクションと呼びます。 図A(断面を除く)が完全に1つの半平面にある割線は、 境界と呼ばれます 。
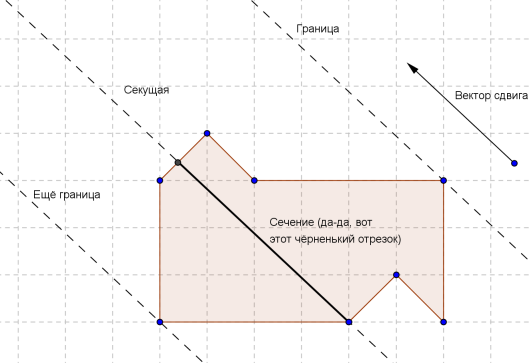
補題1.境界によるセクションには、複数のポイントが含まれている必要があります。
証拠:明らかです。 よくまたはより拡張:私たちは反対から証明します。 この点が図形Bに属する場合、その画像 (つまり、並列転送中に移動する点)は図形Cに属します=>画像は図形Aに属します=>画像はセクションに属します 論争。 この点が図形Cに属している場合、その逆イメージ (並列化されたときに通過する点)は図形Bに属し、同様に同様です。 セクションには少なくとも2つのポイントが必要であることがわかります。
この単純な補題に導かれると、必要な並列転送は垂直軸(画像の現在の方向)に沿ってのみ発生することを理解するのは簡単です。それが他の方向にある場合、境界セクションの少なくとも1つは単一ポイントで構成されます。 これは、せん断ベクトルを精神的に回転させ、境界線に何が起こるかを調べることで理解できます。 垂直並列転送の場合を除外するには、より巧妙なツールが必要です。
補題2.図形Cの境界にある点のプロトタイプは、図形BとCの境界、または図形Bと領域Dの境界にあります。
証拠:明らかではありませんが、今すぐ修正します。 そのような点は図形の境界点と呼ばれ、図形に属する点とそれに属さない点がある限り任意にそれに近いことを思い出させてください。 したがって、図形Cの境界点(Oと呼ぶ)の近くには、図形Cの点と図形Bまたは領域Dに属する他の点の両方があります。図形Bの点のみが点の逆像になります。点Oの逆像(点Oと呼ぶのが論理的です)図Bの点があります。図Bの点の逆像は、Bに属さない任意の点(つまり、図Cの点または領域Dの点のいずれか)にすることができます。 同様に、ドメインDのポイントについても、ポイントOに任意に近いところに、図形Cのポイント(そしてポイントOはBとCの境界上にある)またはドメインDのポイント(そしてBとDの境界上の逆像)があります。 これらすべての手紙をどうにか通り抜けることができれば、補題が証明されることに同意するでしょう。
定理1.図Aのセクションがセグメントの場合、その長さはシフトベクトルの長さの倍数になります。
証明:このセグメントの「遠」端(つまり、反転イメージもセグメントに属する端)を検討します。 この端は明らかに図形Cに属し、その境界点です。 したがって、その逆画像(ところで、セグメント上にあり、シフトベクトルの長さだけ画像から分離されています)は、BとCの境界、またはBとDの境界にあります。BとCの境界にある場合、その逆画像も取得します。 。 次の反転画像がCの境界上になくなり、Dの境界上になるまで、この操作を繰り返します。これは、セクションの反対側で発生します。 その結果、断面をいくつかの小さなセグメントに分割する逆画像のチェーンを取得します。各セグメントの長さは、せん断ベクトルの長さに等しくなります。 したがって、断面の長さはせん断ベクトルの長さの倍数であり、
定理の帰結1.セグメントである2つのセクションは通約可能でなければなりません。
この結果を使用すると、垂直並列転送も消えることを簡単に示すことができます。

実際、断面はかつて3つのセルの長さを持ち、2つの断面は3から2の半分のルートを引いたものです。 明らかに、これらの量は計り知れません。
おわりに
図がA 0であり、2つの等しい図BとCに切断できる場合、Bは平行移動によってCに変換されません。 継続する。