Clever Geek Handbook

魚の群れの行動に基づく人口アルゴリズム

このコミュニティの枠組みの中で、遺伝的アルゴリズムと実際の応用について繰り返し議論されてきました。 この記事では、食べ物を探している魚群の行動に基づいて機能を最適化する比較的新しい方法を共有したいと思います。



はじめに



前世紀の中頃から、特に進化プロセスに関連する自然の生物学的メカニズムをシミュレートする研究が行われてきました。 80年代になって初めて、これらのメソッドの実用的なテストは、計算の複雑さ、複数の端などをもつn項関数を最適化するための効果的なメソッドの必要性に関連して始まりました。 用語について言えば、これらのアルゴリズムは確率的検索エンジンのクラスに属していることに言及する価値があります。 多くのソースでは、行動、知的、メタヒューリスティック、または人口などの定義も見つけることができます。 後者の用語を使用して、アルゴリズムを分類します。 一般的に、このアルゴリズムは次のスキームを使用してより正確に決定できます。



人口アルゴリズムは、次のカテゴリに分類されます。



用語を扱った後、魚群の行動に基づいた個体群最適化アルゴリズムの研究に直接進みます。



アルゴリズム解析



このアルゴリズムは、2008年にFilo（B. Filho）およびNeto（L. Neto）によって提案されました。

すべての母集団アルゴリズムと同様に、入力パラメーターは次のとおりです。フィットネス関数（極値を見つけるために必要な関数）、この関数の研究分野、およびアルゴリズムのパラメーター（少し後で）。 現在のFSSアルゴリズム（Fish S chool S earch）では、検索エリアは、エージェント（魚）が泳ぐ水槽です。 ご存知のように、食べ物の検索では魚は横枠で泳ぎます。したがって、この場合の最終目標は、すべてのエージェントを関数の極値領域にシフトすることです。 一般に、アルゴリズムの操作スキームは次のとおりです。



  1. 人口の初期化（水槽内の魚の分布さえ）
  2. エージェントの食物源への移動（アナロジー：エージェントが機能の極値の方向に進むステップが大きければ大きいほど、彼らはより多くの食物を受け取りました）
  3. 検索完了


詳細が必要です。


「エージェントの移行」の段階は繰り返し実行され、各繰り返しで2つのグループの演算子が実行されます。



  1. 水族館内の移動のためのエージェントを提供する水泳オペレーター。
  2. 水槽の特定の領域の研究の成功を記録する給餌オペレーター。


水族館とその住民が持っているパラメータについて話す時です。

そこで、水族館全体の特徴である次の変数を導入します。

populationSize



サイズ- populationSize



サイズ（学校内の魚の数）。

iterationCount



「エージェントの移行」段階での反復回数

lowerBoundPoint, higherBoundPoint



検索の上下の境界線

individStepStart, individStepFinal



エージェント周辺の食品検索の開始および終了半径を設定します

weightScale



最大エージェント重量。

これらはまさにユーザーが入力するパラメーターです。 それらを使用して、アルゴリズムの精度/実行時間の比率が調整されます。

エージェント自体の特徴は、次の2つの値のみです。

swimStatePos



水泳のさまざまな段階でのエージェントの位置

weight



-現在のエージェントの重量



もちろん、アルゴリズムのソフトウェア実装では、このような変数の数は明らかに十分ではありませんが、今のところ私たちの生活を複雑にすることはありません 。



このコードは、アイドルチャットよりもプログラマにとって重要であることを認識し、次の擬似コードを使用してアルゴリズムを掘り下げます。 



 initialize_randomly_all_fish; while (stop_criterion is not met) { for (each_fish) { individual_movement; evaluate_fitness_function; } feeding_operator; for (each_fish) instinctive_movement; calculate_barycentre; for (each_fish) do { volitive_movement; evaluate_fitness_function; } update_individidual_step; }




注：以下のアルゴリズムの説明はすべて、関数の条件付き最大化の問題を解決するように設計されていますが、関数の最小値を検索する際にこのメソッドが機能しないことを疑うべきではありません。

  1. そのため、既に述べたように、最初のステップは母集団全体を初期化することです：水槽内のエージェントの位置をランダムに選択し（ swimStatePos[0]



    ）、すべての魚のweight=weightScale/2



    最大値の半分（ weight=weightScale/2



    ）に設定します。
  2. 次に、アルゴリズムのメインサイクルが開始されます。これは、「エージェントの食料源への移行」の段階を特徴付けるものです。 この例では、値「反復回数」（ iterationCount



    ）が停止基準として使用されます。
  3. 次に、水泳エージェントの個々の段階が来ます。 それは、自分自身の周りの特定の領域のすべての魚（ individStep



    ）が関数の最適な値を見つけようとするという事実によって特徴付けられます。

    成功した場合、この手順は修正されます。 そうでなければ



    この動きはそうではなかったと信じています。
  4. 今、あなたは水泳の個々の段階で成功を統合する必要があります。 これを行うには、特性「重量」を使用します。 これは、個々のステージの前後の特定のエージェントのフィットネス関数の変化に等しく、母集団間の関数の最大変化によって正規化されています。 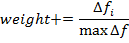。 一般的に言えば、これはこのアルゴリズムの特徴的な機能です。これは、以前の反復で最高のエージェントを覚える必要がないためです。
  5. この後、魚は水泳の次の段階を作ります-本能的に集団です。 魚の群れ全体について、「一般的な移行ステップ」の値が計算されます。 。

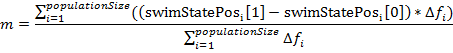    その意味は次のとおりです。各エージェントは全体として全体の人口の影響を受けますが、個々のエージェントの影響は個々の水泳段階での成功に比例します。 次に、母集団全体が計算値mだけシフトされます。



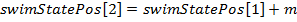
  6. 次の水泳操作の前に、中間ステップを実行する必要があります。つまり、関節全体の重心を計算するためです。 。
  7. 私たち、つまり魚は、水泳の最終段階である集団志向に行きました。 ここでは、前回の反復と比較して母集団の重みがどのように変化したかを調べる必要があります。 増加している場合、人口は関数の最大の領域に近づいているため、その検索を絞り込む必要があり、それにより特性が強化されます。 逆もまた同様です。関節の重量が減少した場合、エージェントは間違った場所で最大値を探しているので、軌道の方向を変えて多様化特性を示す必要があります。



    次の式のcollStep



    の値は、意志的バイアスのステップを担当します。 個々の検索ステップの2倍の値を使用することをお勧めします。 dist



    演算子は、ユークリッド空間の2点間の距離を計算します。



    （ エージェントの位置に関与する値は、n次元ポイントの構造タイプであり、2つのポイントの加算/減算、ポイントと数値の加算/減算、ポイントと数値の乗算/除算、およびポイントの比較演算が定義されています。この幾何学的なナンセンスの場合、これらの量を特定の操作を定義したベクトルデータ型と見なすのが慣例です ）
  8. 反復の最後の演算子は、次の反復の個々の検索ステップの線形減少です。 実際、これはすでに検索効率を高めるための標準FSSアルゴリズムの修正であり、次の式で実行されます。




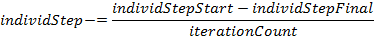
実装とテスト



実装


このアルゴリズムは、私のコースワーク（「魚の群れの行動に触発された最適化プログラム」）の基礎となり、4月26日に国防で発表されました。 多分誰かがタームペーパーがこんなに早く取られた理由に興味を持つだろう。 苦労することなく、これはすべて、高等経済学部（PI）の生物学部（PI）の学生を追放するための計画の一部であり、その結果、年間30％（コインの裏側）の控除が脅かされますプロパガンダのスローガンは、「私たちはすべての人を受け入れ、必要に応じて自費で座席の代金を支払う」と誇示しています。 コースワークの期間のフレームワーク内で、実装はC＃4.0で実施され、OpenTKライブラリ（.NETのOpenGLラッパーを表す）がグラフィックコンポーネントとして選択され、ユーザー定義関数は前にハブに実装されたライブラリを使用して解析されました 。 残念ながら、ソースコードをレイアウトすることはできません（コードは完璧とはほど遠い、自分で何度も気づきました）が、プログラム自体はすべての裁量で提供します（記事の最後のリンク）。 それまでの間は、メインウィンドウのスクリーンショットのみをご覧ください。







テスト中


母集団ベースのアルゴリズムの場合、テストの結果は入力パラメーターに大きく依存するため、テストは魅力的なものです。 この記事の一部として、次の2つのグラフを検討します。



    • 検索範囲：（-100; -100）から（100; 100）
    • 反復回数：100
    • 人口規模：50
    • 最初の個々のステップ：10
    • 最終個別ステップ：0.1
    • 最大魚重量：50


    したがって、アルゴリズムの終了までに、関数の最大値は9.999978 ...であり、平均値は9.999148 ...です。平均値の変化のグラフは次のとおりです。



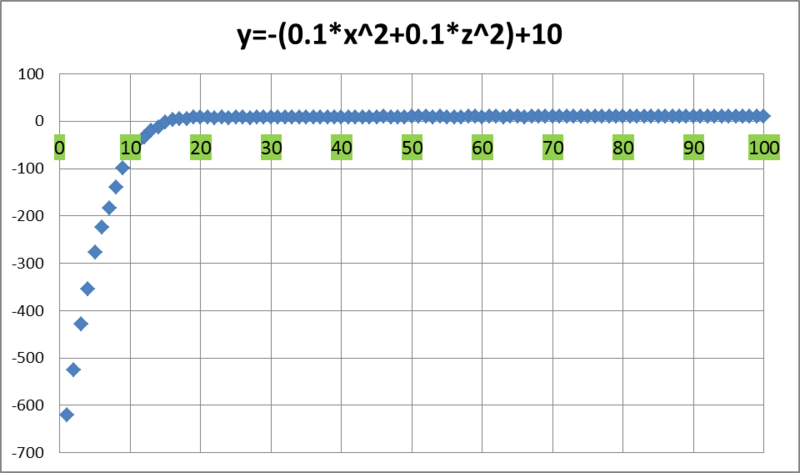
    つまり、すでに15回目の繰り返しで、魚の群れはOY軸に沿って正の半平面にありました。 そして、48回目の反復以降、関数の平均値は9未満になりませんでした。 そして、これが何が起こっているかの全体像です（氷山の一角からの眺め）：







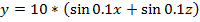
    • 検索範囲：（-100; -100）から（100; 100）
    • 反復回数：100
    • 人口サイズ：50
    • 最初の個々のステップ：10
    • 最終個別ステップ：0.1
    • 最大魚重量：50




    アルゴリズムの終わりまでに、関数の最大値は19.999996 ...で、平均は19.9994 ...でした。平均値のダイナミクスは次のとおりです。





    すでに42回の反復から、関数の平均値は19以上のレベルにとどまりました。 アルゴリズムが複数の極端な機能を処理する方法のアニメーション（Habrastorageの場合、ファイルが大きすぎるため、画像表示に問題がある可能性があります）：



ソース







PS


記事を読んでくれてありがとう！ コメントでご質問にお答えさせていただきます。



UPD：ソースコードを追加しました。


More articles:


All Articles