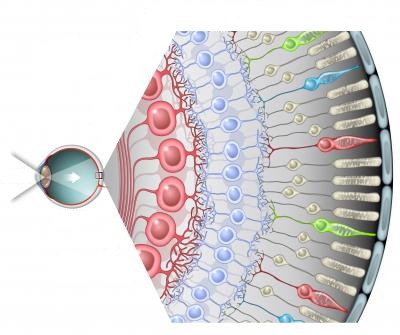
こんにちは この投稿では、 制限付きボルツマンマシンで2種類の正則化をテストする実験を行います。 結局のところ、RBMは、ニューロンのモーメントや局所場などのモデルパラメーターに非常に敏感です（すべてのパラメーターの詳細については、 ジェフリーヒントンのRBM実用ガイドを参照してください）。 しかし、全体像とこのようなパターンを取得するために、もう1つのパラメーターが欠落していました-正則化。 限られたボルツマンマシンは、一種のマルコフネットワークと別のニューラルネットワークの両方として扱うことができますが、さらに深く掘り下げると、視覚との類推がわかります。 網膜から視神経を介して情報を受け取る一次視覚野のように（生物学者はそのような単純化を許してくれます）、RBMは入力画像で単純なパターンを探します。 類推はこれで終わりではありません。非常に小さくてゼロの重みを重みがないと解釈すると、各隠れたRBMニューロンが受容野を 形成し、訓練されたRBMから形成された深いネットワークが単純な画像からより複雑な特徴を形成することがわかります; 原則として、脳の視覚皮質は似たようなことに関与していますが、おそらくもっと複雑です=）
L1およびL2正則化
おそらく、モデルの正則化とは何かを簡単に説明することから始めます—モデルの複雑さの目的関数にペナルティを課す方法です。 ベイジアンの観点から見ると、これはモデルパラメーターの分布に関する事前情報を考慮する方法です。 重要な特性は、正則化がモデルの再トレーニングを回避するのに役立つことです。 モデルパラメーターをθ= {θ_i}、i = 1..nとして示します。 最終目的関数はC =η（E +λR）です 。ここで、 Eはモデルの主な目的関数、 R = R（θ）はモデルパラメーターの関数、 thisとlambdaはそれぞれ学習速度と正則化パラメーターです。 したがって、最終目的関数の勾配を計算するには、正則化関数の勾配を計算する必要があります。
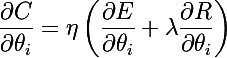
ルートがLpメトリックにある2種類の正則化を検討します 。 正則化関数L1とその導関数は次のとおりです。
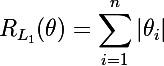
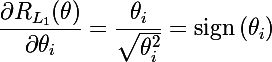
L2正則化は次のとおりです。
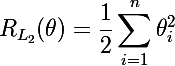
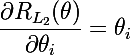
両方の正則化方法は、重量の大きな値、最初の場合は重量の絶対値、2番目の場合は重量の2乗のモデルを細かく調整するので、重量の分布は、中心がゼロで大きなピークを持つ正常値に近づきます。 L1とL2のより詳細な比較については、 こちらをご覧ください 。 後で見るように、重みの約70％は10 ^（-8）未満になります。
RBMの正則化
前年の投稿で、 C＃でのRBM実装の例を説明しました 。 正則化がどこに埋め込まれているかを示すために、同じ実装に依存しますが、最初は式です。 RBMトレーニングの目標は、復元された画像が入力と同一になる可能性を最大化することです。
一般的に、アルゴリズムでは確率対数が最大化され、ペナルティを導入するために、得られた確率から正則化関数の値を減算する必要があります。その結果、新しい目的関数は次の形式を取ります。
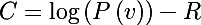
パラメータに関するこのような関数の導関数は次のようになります。
対照的発散アルゴリズムは正相と逆相で構成されているため、正則化を追加するには、正相の値から正相の値から正則化関数の導関数の値を減算するだけで十分です。
正相と負相
#region Gibbs sampling for (int k = 0; k <= _config.GibbsSamplingChainLength; k++) { //calculate hidden states probabilities hiddenLayer.Compute(); #region accumulate negative phase if (k == _config.GibbsSamplingChainLength) { for (int i = 0; i < visibleLayer.Neurons.Length; i++) { for (int j = 0; j < hiddenLayer.Neurons.Length; j++) { nablaWeights[i, j] -= visibleLayer.Neurons[i].LastState * hiddenLayer.Neurons[j].LastState; if (_config.RegularizationFactor > Double.Epsilon) { //regularization of weights double regTerm = 0; switch (_config.RegularizationType) { case RegularizationType.L1: regTerm = _config.RegularizationFactor* Math.Sign(visibleLayer.Neurons[i].Weights[j]); break; case RegularizationType.L2: regTerm = _config.RegularizationFactor* visibleLayer.Neurons[i].Weights[j]; break; } nablaWeights[i, j] -= regTerm; } } } if (_config.UseBiases) { for (int i = 0; i < hiddenLayer.Neurons.Length; i++) { nablaHiddenBiases[i] -= hiddenLayer.Neurons[i].LastState; } for (int i = 0; i < visibleLayer.Neurons.Length; i++) { nablaVisibleBiases[i] -= visibleLayer.Neurons[i].LastState; } } break; } #endregion //sample hidden states for (int i = 0; i < hiddenLayer.Neurons.Length; i++) { hiddenLayer.Neurons[i].LastState = _r.NextDouble() <= hiddenLayer.Neurons[i].LastState ? 1d : 0d; } #region accumulate positive phase if (k == 0) { for (int i = 0; i < visibleLayer.Neurons.Length; i++) { for (int j = 0; j < hiddenLayer.Neurons.Length; j++) { nablaWeights[i, j] += visibleLayer.Neurons[i].LastState* hiddenLayer.Neurons[j].LastState; } } if (_config.UseBiases) { for (int i = 0; i < hiddenLayer.Neurons.Length; i++) { nablaHiddenBiases[i] += hiddenLayer.Neurons[i].LastState; } for (int i = 0; i < visibleLayer.Neurons.Length; i++) { nablaVisibleBiases[i] += visibleLayer.Neurons[i].LastState; } } } #endregion //calculate visible probs visibleLayer.Compute(); } #endregion } #endregion
実験に進みます。 テストデータとして、 前回の投稿の前年と同じセットが使用されました。 すべてのケースで、トレーニングは正確に1000時代に行われました。 見つかったパターンを視覚化する2つの方法を示します。最初のケース（グレートーンの画像）では、暗い値は最小重量値に対応し、白い値は最大値に対応します。 2番目の図では、黒はゼロに対応し、赤の成分の増加は正の方向の増加に対応し、青の成分の増加は負の方向に対応します。 また、重みと小さなコメントの分布のヒストグラムを示します。
正則化なし
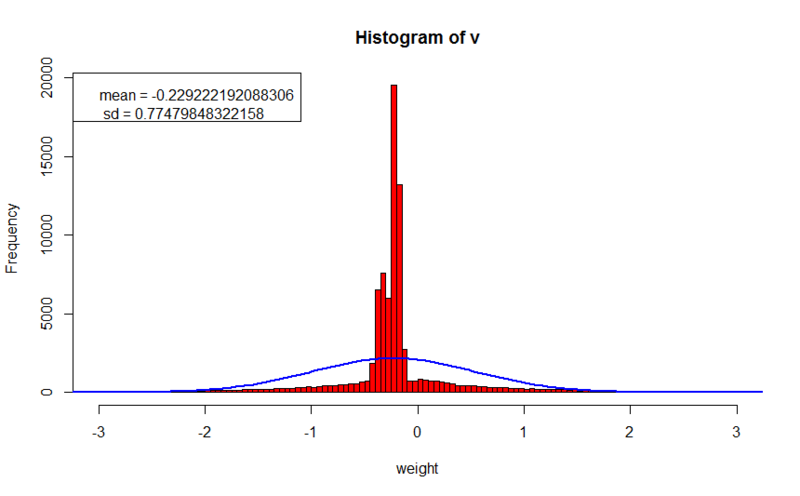
- トレーニングセットのエラー値：0.188181367765024
- 相互検証セットのエラー値：21.0910315518859
パターンは非常にぼやけており、分析が困難であることが判明しました。 バランスの平均値は左にシフトし、バランスの絶対値は2以上に達します。
L2正則化
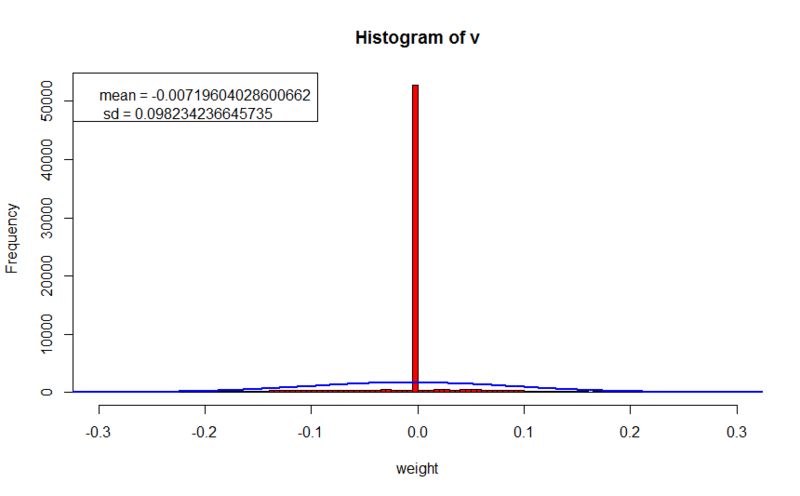
- トレーニングセットのエラー値：10.1198906337165
- 交差検定セットのエラー値：23.3600809429977
- 正則化パラメーター：0.1
ここでは、より鮮明な画像を観察します。 一部のキャラクターが文字のいくつかの機能を実際に考慮していることはすでにわかりました。 トレーニングセットのエラーは正則化なしで学習する場合よりも100倍悪いという事実にもかかわらず、交差検証セットのエラーは最初の実験よりもそれほど大きくないため、見慣れない画像でのネットワークの一般化能力はそれほど低下していないことを示唆していますエラー計算には正則化関数の値が含まれていなかったため、以前の経験と値を比較できます）。 重みはゼロ付近に集中しており、絶対値で0.2を大きく超えることはありません。これは、前の実験の10倍です。
L1正則化
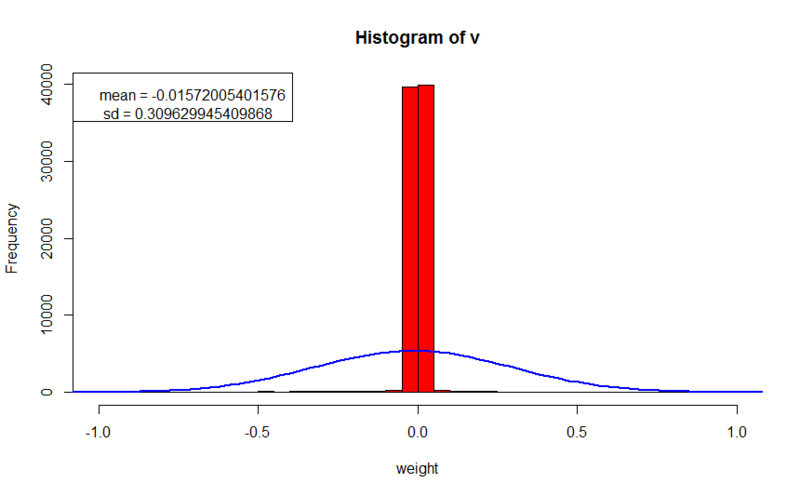
- トレーニングセットのエラー値：4.42672814826447
- 相互検証セットのエラー値：17.3700437102876
- 正則化パラメーター：0.005
この実験では、明確なパターン、特に受容野を観察します（青赤のスポットの周りでは、すべての重みはほぼゼロです）。 パターンを分析することもできます。たとえば、Wからのエッジ（最初の行、4番目の画像）、または入力画像の平均サイズを反映するパターン（5番目の行、8および10の画像）に気付くことができます。 トレーニングセットの回復エラーは最初の実験よりも40倍悪いですが、L2正則化よりも優れていますが、未知のセットのエラーは以前の両方の実験よりも優れており、これはさらに優れた一般化能力を示しています。 重みもゼロ付近に集中しており、ほとんどの場合、それをあまり超えません。 正則化パラメーターの大きな違いは、L2の勾配を計算するときにパラメーターに重み値が乗算されるという事実によって説明されます。原則として、これら2つの数値は1未満です。 ただし、L1では、パラメーターに| 1 |が乗算され、最終値は正則化パラメーターと同じ順序になります。
おわりに
結論として、BSRは実際にはパラメーターに非常に敏感であると言いたいと思います。 そして、主なことは、解決策を見つける過程で分解することではありません-）最後に、L1正則化で訓練されたRBMの1つの拡大画像を、5000時代にわたって提供します。
更新 ：
最近、フルセットの大文字4フォント3スタイルでrbmを教え、L1正則化の5000回の反復中に約14時間かかりましたが、結果はさらに面白く、機能はさらにローカルできれいになりました
