ビットマップ画像を任意の角度で回転させるために、高速ではあるが最適ではないアルゴリズムが開発されており、品質を損なう実用的な目的に適した近似を提供します（たとえば、 これ ）
かなり昔、純粋にスポーツの興味から、ビットマップ画像を任意の角度に最も正確に回転させる作業に興味がありました。 残念ながら、既製のアルゴリズムはどこにも見つからなかったので、自分でやらなければなりませんでした。 たとえ最終的に「自転車を発明した」としても、その結果は共有できるほど興味深いものであるように思われます。
以下では、最小の損失で任意の中心に対して任意の角度でラスター画像を正確に回転させるアルゴリズムを検討します。
Kharchenko Vladislav Vladimirovichの支援に感謝します。
アルゴリズム
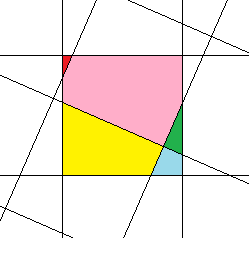
上記の図からわかるように、ビットマップ画像の回転後、最終画像の各ピクセルの色は、対応する「フラグメント」の面積に比例して、元の画像のいくつかのピクセルのいくつかの「フラグメント」の色の追加によって決定されます。 したがって、一般的に言えば、問題の解決策は、元の画像の各ピクセルのすべての「フラグメント」の領域を見つけ、対応する「フラグメント」の色から最終画像の各ピクセルの色を収集することです。
元の画像のピクセルモデルとして、side = 1の正方形を使用し、次の角度表記を使用します。
i1は右端の角です。
i2は最も低い角です。
i3は左端の角です。
i4は一番上のコーナーです。
最終的な画像のモデルは、ライン間の距離が1の平行な水平線と垂直線のグリッドになります。
この表現のラスターイメージの回転中心の座標は、任意の実数のペアとして表現できます。 つまり、問題の回転の中心は、ピクセルの幾何学的な中心ではなく、グリッド線の交点ではなく、デカルト座標の任意の点にある可能性があります。
ビットマップ画像を回転させると、各ピクセルの正方形が同じ角度（このピクセルの中心に対して）回転するため、1つのピクセルの問題を解決してから、元の画像の各ピクセルに結果のソリューションを適用します。
ラスターイメージの回転は、2つの部分に分割できます。
1.元の画像の各ピクセルの正方形の、この正方形の中心に対する特定の角度の回転。
2.正方形が最終画像のグリッド上の最終位置を占めるように、画像の回転中心に対する画像の回転角に応じたピクセルの正方形の中心のオフセット。
この場合、最終画像のグリッドは、元の画像の各ピクセルの正方形を4、5、または6個の「断片」に切り取ります。
結果として生じるさまざまなオプションを体系化するために、ソース画像のピクセルの正方形と最終画像のグリッドのすべての種類の交点の分類法をコンパイルする必要がありました。 基本的に異なるオプションは23のみでした。
規則は次のとおりです。
-セル内の数字は、画像の回転後に最終画像のグリッドのこのセルに落ちたピクセルの正方形の角度の数を示します。
-緑色は、ピクセルセクションが取得され、「フラグメント」によってそこに残されることが保証されているセルを示します。
-黄色は、条件に応じて、正方形の角ではなく正方形の辺によって形成されるピクセル正方形の「断片」 が入る（または入らない）セルを示します。
明確にするために、オプションNo.3の可能なバリエーションの1つを示します。
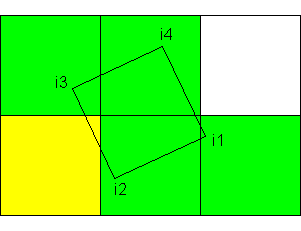
ご覧のとおり、右上のセルにはピクセルの「フラグメント」は含まれていませんが、他の回転条件では含まれている可能性があります。
読者に詳細な幾何学的計算を負担させないために、これら23種類すべてで、元の画像のピクセルが「断片」に切り分けられ、その面積は4つの式を組み合わせて簡単に計算できると言います。 これらの式を以下に示します。 赤は、ピクセルの正方形を切り取る最終画像のグリッド線を示します。 式によって面積が計算される面積は、黄色で網掛けされています。
フォーミュラ1
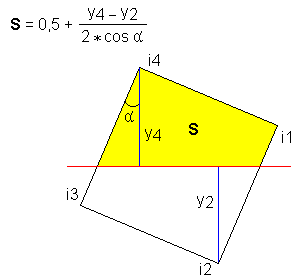この式は、「フラグメント」の最終面積の計算には使用されませんが、ピクセル全体の面積= 1であることがわかっているため、補助中間面積の迅速な計算に使用すると便利です。
最終画像のグリッド上の正方形の角から省略された高さは、これらの高さの計算がピクセルの正方形の対応する角の座標の数値の小数部分の瞬間的な選択に短縮されるという単純な理由で、すべての式で入力変数として使用されます。
フォーミュラ2
この式は、オプション1および2でのみ使用されます。
フォーミュラ3
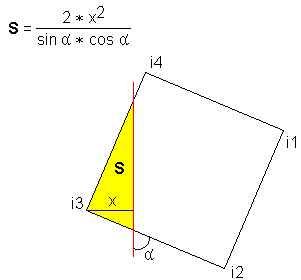頻繁に使用される式は、すぐに計算できるという点で非常に優れています。 回転角度は各ピクセルで同じであるため、すべてのピクセルを処理する前に、すべての三角関数を1回カウントし、ループでこれらの値を定数として使用できます。
フォーミュラ4
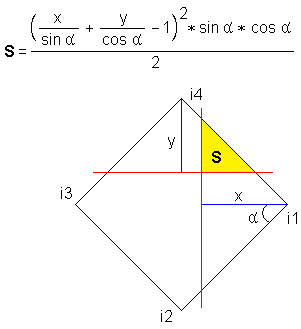この式は2つのステップで計算されます。 最初に、括弧内の式が評価されます。 正の値をとる場合、面積が計算されます。 値が負の場合、グリッドの角度と正方形の辺によって形成される「スプリンター」がピクセルをカットオフせず、さらに計算を行う意味がないことを意味します。
上記のすべてを考えると、一般的に言えば、アルゴリズムは次のようになります。
1.元の画像をコンピューターのメモリに読み込みます。
2.最終画像のサイズをピクセル単位で計算します。
3.中間の2次元配列を作成します。その各要素には、浮動小数点数の形式で3つのRGB色成分が含まれています。 配列の次元は、最終画像のサイズに等しくなります。
4.元の画像のすべてのピクセルを順番に並べ替えます。 それらをそれぞれ所定の角度だけ回転させて、最終画像のグリッドに配置し、ピクセルの正方形の角の4つの座標を計算します。 23のオプションに従ってピクセルを分類し、「フラグメント」の領域を考慮します。 これらの「フラグメント」の面積に比例して、結果の「フラグメント」の色を中間配列の対応する要素に追加します。
5.元の画像のすべてのピクセルを処理した後、中間配列のRGB値を各要素の整数値に丸め、これらの整数値に基づいてBMP形式の最終画像を作成します。
プログラム
上記のアルゴリズムに基づいて、Windows用のプログラムが作成されました。 Object Pascalのソースコードとコンパイルされた実行可能ファイルは、 ここからダウンロードできます 。
プログラムインターフェイス。
「開く...」ボタンをクリックすると、BMPファイルを選択するためのダイアログが開きます。 24ビットパレットのみのビットマップがサポートされています。 開いている画像がウィンドウに表示されます。 ファイルの完全なタイトルと画像サイズがウィンドウのタイトルに表示されます。
フィールド「角度」では、回転角度を度数で設定します-任意の正数。
小数を入力するときは、ピリオドとコンマの両方を小数点記号として使用できます。
ラジオボタン「CW」と「CCW」は、それぞれ「時計回り」と「反時計回り」の回転方向を指定します。
「背景色」ブロックでは、画像の境界ピクセルを混合する背景色を設定できます。 デフォルトの背景色は黒です。
「中心X」および「中心Y」フィールドに、回転中心の座標が設定されます。 原点は画像の左上隅にあり、Yは下に向かって増加することに注意してください。 デフォルトでは、回転の中心は読み込まれた画像の幾何学的中心に設定されます。
「回転」ボタンを押すか、Enterキーを押すと、画像が所定の回転中心に対して所定の角度だけ回転し、ウィンドウに表示されます。 90°の倍数の角度で画像を回転させることは、元の画像のピクセルの座標を単純に変換する単純なスキームに従って実装されますが、「Center X」と「Center Y」の値は無視されます。
アルゴリズムの実行時間（秒）は、[回転]ボタンの下に表示されます。
「保存...」ボタンを使用すると、回転した画像をBMPファイルに保存できます。
最終画像がウィンドウに収まらない場合-StretchBlt API関数によってウィンドウの境界に合わせて調整される-したがって、保存されたBMPファイルからのみ大きな画像の実際の品質を評価することができます。
画像を別の角度に回転させるために、画像を再ロードする必要はありません-選択したファイルの画像は回転し、現在ウィンドウに表示されていません。
4コアの2.67 GHzプロセッサを搭載したマシン上の1024 x 768の寸法の画像は、このプログラムによって、平均して約0.5秒で任意の角度で回転します。 4000 x 4000の寸法の画像-約10秒。 異なる角度でのアルゴリズムの動作時間は、それぞれ異なる時間で費やされる領域の計算のために、異なる角度の画像が異なる数の「断片」に分割されるという事実により異なる場合があります。
浮動小数点数の形式で最終画像のピクセルの色情報を含む中間配列は拡張（10バイト）として実装されるため、大きな画像（約5000 x 5000ピクセル以上）を処理するとメモリオーバーフローエラーが発生する可能性があります。 精度の低いデータ型を適用し、数値の整数部を最終ビットマップにすぐに保存し、小数部のみを補助配列に残すことにより、状況を改善することができます。
結果
Photoshopで実装された精密アルゴリズムと画像回転アルゴリズムの動作の比較分析を行いましょう。
テスト1
最初のテストでは、非常に単純な画像を撮影しました-太さ1ピクセル、長さ10ピクセルの黒の水平線、寸法が100 x 100ピクセルの白い正方形の中心からのオフセット：
その後、座標（0、0）が時計回りに3°の点を基準にしてこの画像を回転させました。 私の実験で判断すると、Photoshopはこの特定の点を基準にして画像を回転させるため、点（0、0）が選択されました。 比較結果は次のとおりです（24倍に増加）。
精密アルゴリズム
Photoshop 7.0.1
Photoshop CS6（64ビット）
Photoshopアルゴリズムはよりコントラストのある画像を提供し、精密アルゴリズムは画像を多少「ぼかす」。 しかし、一般的に、視覚的な評価では、結果はほぼ同じです。 途中で、Photoshopで実装された回転アルゴリズムは10年間で大きな変化を受けていません。
テスト2
2番目のテストでは、標準のWin7ディストリビューションからチューリップを選択しました。
この画像を幾何学的中心に対して時計回りに5°回転させた後、RGBチャンネルのコンテキストですべてのピクセルの色を合計しました。 精度アルゴリズムとPhotoshopアルゴリズムの結果は次のとおりです。
オリジナル | 精密回転
| 精密回転
| Photoshop CS6 |
| R = 33381406
G = 27933900 B = 11239213 | R = 33381406.0000004 （ 〜0 ）
G = 27933899.9999997 （ 〜0 ） B = 11239212,9999999 （ 〜0 ） | R = 33382786 （1380）
G = 27933920 （20） B = 11238086 （-1127） | R = 33387726 （6320）
G = 27950823 （16923） B = 11245937 （6724） |
正確に回転した後、丸める前の画像の色は、実際には変更されていません-これは予想されることです。
この特定の場合の最大の違いは、PhotoshopアルゴリズムのチャネルGにあります。 パーセンテージで見ると、この偏差はわずか0.06％であるため、「目で」目立つことはありませんが、完璧主義の理由から、Photoshopの結果は精密アルゴリズムの結果よりも悪くなります。
精度アルゴリズムの各ピクセルの色をBMP形式に必要な整数値に丸めると、色情報の一部が不可逆的に破壊されることに注意することが重要です。
2つのアルゴリズムを視覚的に比較するために、画像の拡大部分を示します。
Photoshop'om：それぞれ時計回りに5°回転
および精度アルゴリズム：
比較分析により、Photoshopは画像のコントラスト要素をよりよく保持しますが、同時に歪んだ色の「ハロー」を作成します。 精度アルゴリズムは色を歪ませませんが、同時に画像をいくらかぼかすことができます。
結論
1.正確かつ任意の角度でのビットマップ画像の比較的速い回転が同時に可能です。 私にとって、プロのグラフィックエディターには、ユーザーがもう少し時間をかけて画像を非常に正確に回転させるオプションがない理由は疑問のままです。
2.考慮されるアルゴリズムの極端な精度にもかかわらず、逆画像変換、すなわち 正確な色の値（浮動小数点数の形式）を丸めると、色情報の一部が不可逆的に破壊されるため、品質を損なうことなく反対の角度に回転することはできません。
3.コントラストの細部の視覚的知覚の観点から、最良の結果はPhotoshopの最適なアルゴリズムによって提供されます。 精度アルゴリズムは、画像の色に関する最大の情報を維持することが重要な場合に適用する意味があります。
UPD：実際の使用のために、最終画像の各ピクセルについて、元の画像の必要なすべてのピクセルを順次計算し、色の丸めをすぐに実行する単純化されたアルゴリズムを実装するプログラムを作成しました。 その後のみ、最終画像の次のピクセルが計算されます。 この場合、プログラムはソース画像の単一ピクセルに数回アクセスします。 したがって、計算時間は平均で1.7倍になりましたが、このバージョンのアルゴリズムのメモリはビットマップの保存にのみ使用されるため、大きな画像を扱うことができます。 ここからプログラムとソースをダウンロードします 。