 「抵抗->温度」関数のグラフをマイクロコントローラーに読み込むためのインターフェイスを作成する必要がありました(グラフをいくつかのポイントに設定してから補間することにしました)。 その過程で、グラフは非常に非線形であることがわかりました(180オーム-> 100 o 、6,000オーム-> 0 o 、30,000オーム-> -30 o )。 だから、私は対数スケールのトピックに飛び込む必要がありました...そして、私は必要なものを見つけられなかったので、すぐに現れました。 そして、そのような問題の数学(およびC ++での実装)を理解する必要がありました。 素晴らしい-それはそのような必要なトピックのようですが、塗装されていません! まあ、大丈夫-脳はきしみ、大学の高等数学を思い出し、プログラムが書かれました。 ここで試練を説明することにしました-誰かが役に立つかもしれません。
「抵抗->温度」関数のグラフをマイクロコントローラーに読み込むためのインターフェイスを作成する必要がありました(グラフをいくつかのポイントに設定してから補間することにしました)。 その過程で、グラフは非常に非線形であることがわかりました(180オーム-> 100 o 、6,000オーム-> 0 o 、30,000オーム-> -30 o )。 だから、私は対数スケールのトピックに飛び込む必要がありました...そして、私は必要なものを見つけられなかったので、すぐに現れました。 そして、そのような問題の数学(およびC ++での実装)を理解する必要がありました。 素晴らしい-それはそのような必要なトピックのようですが、塗装されていません! まあ、大丈夫-脳はきしみ、大学の高等数学を思い出し、プログラムが書かれました。 ここで試練を説明することにしました-誰かが役に立つかもしれません。
この記事では理論(および基本的な仮想クラス)について説明し、次ではQtを使用して特定の実装を取り上げます。
注意:テキストには多くのグラフィックがあります!
タスクはどこから成長しますか
一般に、 私はアイドル速度制御を行う必要があります -エンジン温度に応じてアイドリング時に特定の速度を維持しなければならないような車のようなものです。 彼女はステッパーモーターでダンパーを調整することでそれらをサポートします。
一般的に、現在の温度を知る必要があります。 サーミスタを使用して、定期的に測定することにしました。 電圧降下を測定します-抵抗を取得します。 さらに、テーブルから(マイクロコントローラであるため)、必要な速度を取得します。
このテーブルを設定する必要があります(このため、プログラムはQtを使用して作成されます)。 「抵抗=>温度」という点がいくつかあります。 各ADCコードに適切な温度を取得する必要があります(多くの吸収値に対して)。 車によって異なるため、これらの値は異なる可能性があるため、画面上でテーブルを確認し、カーブ上のいくつかのポイントを設定する必要があります。
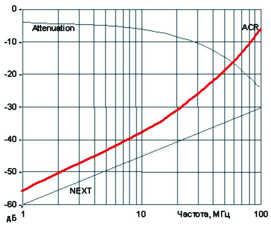
その過程で、このグラフは明らかに対数スケールになることが判明しました。 そのため、表示する必要があります。 これを行う方法-読んでください。
問題の声明
必要なものをさらに詳しく説明しましょう。
- 関数の割り当て -グラフが作成されるいくつかのポイントを設定する必要があります。 一般に、 補間を思い出します。
- 関数のプロット -はい、はい、 Qwtについて知っています 。 私は彼をあまりよく知らないのかもしれません。なぜなら、彼には次の可能性が見つからなかったからです。
- インタラクティブなタスク定義 -スケールの現在の画面座標内で、関数が構築されるポイントを画面上で移動し、実際の値に変換する必要があります。
- 線形/対数スケール -値は私が書いたものと同じなので、スケールを変更できるようにしなければなりませんでした。 そして、両方とも同時に。
ここにTKがあります...まあ、何も、私はそれをしませんでした! 私もあなたを助けさせてください。
はい、潜るまで-CodeCogsのEquation Editorに感謝します! 彼らの助けを借りて、Microsoft Equation Editorを使用せずにすべての数式を作成したことは有名です。その後、ここに挿入してグラフィックスにエクスポートする必要があります。 ところで、 ロシア語の編集者もいます。 一般的に、私はお勧めします!
さて、数式の代わりに空の四角が表示される場合、これは方程式エディターの「ありがとう」です...
添付のExcelファイル
この記事を書いたとき、Excelスプレッドシートのすべての計算式を作成し、数式でチェックしました。 それは非常に便利であることが判明しました。 そして、私はそれを公共の使用のために出すことにしました。 以下のページはセクションごとにリストされています。 各ページで、変更できるパラメーターは、背景が黄色のセルとしてマークされています。 残りのセルはそのままにしておくのが最適です。 ただし、すべての式は安全に監視できます。 ファイルをダウンロードして、健康状態を試してください! ファイルに問題がある場合-書き込み、送信します。
機能依存
そのため、いくつかの依存関係があります。
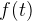 。 ここにあります
。 ここにあります  -グラフの水平軸、
-グラフの水平軸、 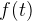 -垂直。 私の場合
-垂直。 私の場合  抵抗の値でした
抵抗の値でした 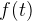 -温度。
-温度。
どうして
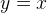 ? やっぱりこんな感じ? それはそうですが、最も単純なケース
? やっぱりこんな感じ? それはそうですが、最も単純なケース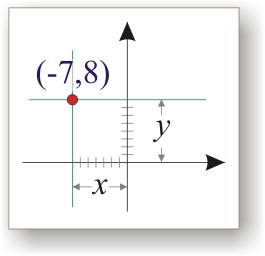
 平面上の点の座標です。 簡単にするために、 デカルト座標系を使用することにします。
平面上の点の座標です。 簡単にするために、 デカルト座標系を使用することにします。 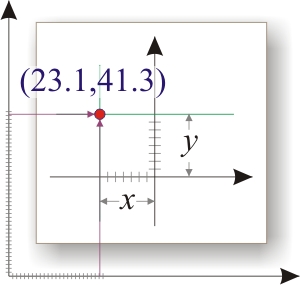 この非常に座標系を紙に描き、そこにポイントを入れると、すべてがうまくいきます。 本当に-彼らはセンターを選び、定規でそれをここに置き、そこに。 しかし、あるプログラムでグラフを作成するとき、微妙なことが始まります-ゼロとみなすべきものは何ですか? 「+」と見なすもの、および「-」とは何ですか? この記事のグラフィックスをCorelDRAWで描画します。中心は左下から考慮されます(必要に応じて移動できます)。
この非常に座標系を紙に描き、そこにポイントを入れると、すべてがうまくいきます。 本当に-彼らはセンターを選び、定規でそれをここに置き、そこに。 しかし、あるプログラムでグラフを作成するとき、微妙なことが始まります-ゼロとみなすべきものは何ですか? 「+」と見なすもの、および「-」とは何ですか? この記事のグラフィックスをCorelDRAWで描画します。中心は左下から考慮されます(必要に応じて移動できます)。
 また、スケジュールはどういう単位で行われますか? センチメートルで? なんで? 次のステップは、Qtツールを使用したC ++での実装です。そこで、デフォルトでゼロに設定されたQWidgetウィンドウを作成します。これは左上にあります。 測定単位は画面のピクセルです。
また、スケジュールはどういう単位で行われますか? センチメートルで? なんで? 次のステップは、Qtツールを使用したC ++での実装です。そこで、デフォルトでゼロに設定されたQWidgetウィンドウを作成します。これは左上にあります。 測定単位は画面のピクセルです。
さて、この美しい推論はすべて線形スケールに有効であり、地平線上に対数が迫っていることを忘れないでください。 そこで悪魔は何が起こるかを知っています!
しかし、これはポイントです。 そして、ある種の線、またはむしろ、たくさんの線があります。 どんな変換がありますか?
だからこそ、 機能の依存関係と座標変換を最初から明確に分離する必要があります。
それでは、次のことに同意しましょう。 機能的な依存関係によって記述される抽象的なプロセスがあります
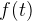 。 画面に表示されるとき、座標への変換が使用されます
。 画面に表示されるとき、座標への変換が使用されます 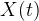 そして
そして 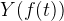 。
。
しかし、今のところ、座標は脇に置いておきます-関数を設定する必要がありますか(TKを思い出してください)? そして、これらの非常に抽象的な座標で尋ねます
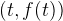 。 これが私たちがやることです。
。 これが私たちがやることです。
補間
私の場合、多くのポイントが知られていました
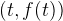 :
:
 、Ω 、Ω | 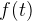 、˚ 、˚ |
|---|---|
| 180 | 100 |
| 6,000 | 0 |
| 30,000 | -30 |
それほど暑くなく、大きなテーブルは複雑ですが、明らかに空の場所がたくさんあります。 そして、60°、-40°、...に対応する抵抗は何ですか? 一般に、不足しているポイントを記録する必要があります。 そして、これは補間 、 近似 、 外挿に役立ちます。 ただし、心配する必要はありません。目にとっては補間だけで十分です。
 多くの補間方法がありますが、ここではすべてを検討しません。 個人的には、最初はラグランジュ補間多項式が好きでした。 計算と実装、および構成は非常に簡単です。 そこでは、一連の
多くの補間方法がありますが、ここではすべてを検討しません。 個人的には、最初はラグランジュ補間多項式が好きでした。 計算と実装、および構成は非常に簡単です。 そこでは、一連の  ビューポイント
ビューポイント  (ここでしばらくの間、フォームのポイントのタスクに戻ります
(ここでしばらくの間、フォームのポイントのタスクに戻ります 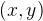 -したがって、数学で受け入れられます)。
-したがって、数学で受け入れられます)。
多項式は次のように計算されます
 どこで
どこで  。
。
数学が怖い? うーん...さて、私はC ++で書きます:
typedef qreal Real; Real Lagranj (Real X) { static const int n = 3; static Real y[n] = {100, 0, -30}; static Real x[n] = {180, 6000, 30000}; Real L, l; int i, j; L = 0; for (i = 0; i < n; ++i) { l = 1; for (j = 0; j < n; ++j) if (i != j) l *= (X - x[j]) / (x[i] - x[j]); L += y[i] * l; } return L; } int main (int argc, char *argv[]) { Real y; y = Lagranj (180); y = Lagranj (500); y = Lagranj (1000); y = Lagranj (6000); y = Lagranj (10000); y = Lagranj (30000); y = Lagranj (0); y = Lagranj (100000); }
ご覧のとおり、すべてが非常に簡単です(多項式が簡単になる可能性があります)。
ラグランジュ多項式のもう1つの大きな利点は、Excelテーブルで簡単にモデル化できることです。
しかし、これらの多項式は他の多項式と同様にグラフに振動を示すため、すべてが少し悲しくなりました。 つまり、直線-一定の値を与えることはできません。 私の場合は、MUSTを構成できませんでした-明らかに無効な数字に曲がっていました。 したがって、私はそれらを放棄しなければなりませんでした...
 Corelでの作業中、私はベジェ曲線に非常に精通していました-また、表データの非常に便利でシンプルなプレゼンテーション。 プログラミングでの実装は非常に簡単です。 ただし、これは補間ではなく、近似です。これは、ここで曲線を目的の形式に合わせる必要があるためです。
Corelでの作業中、私はベジェ曲線に非常に精通していました-また、表データの非常に便利でシンプルなプレゼンテーション。 プログラミングでの実装は非常に簡単です。 ただし、これは補間ではなく、近似です。これは、ここで曲線を目的の形式に合わせる必要があるためです。
 その結果、自分の機能を注意深く見て、 区分的線形補間(与えられた線の間の直線)が非常にうまくいくことに気付きました。 風水ではありませんが、簡単に実装でき、便利にカスタマイズできます。
その結果、自分の機能を注意深く見て、 区分的線形補間(与えられた線の間の直線)が非常にうまくいくことに気付きました。 風水ではありませんが、簡単に実装でき、便利にカスタマイズできます。
数学の言語では、私たちはポイントの間です
繰り返しますが、C ++では、次のようになります。
typedef qreal Real; Real Linear (Real X) { static const int n = 3; static Real y[n] = {100, 0, -30}; static Real x[n] = {180, 6000, 30000}; static Real k[n] = { (y[1] - y[0]) / (x[1] - x[0]), (y[2] - y[1]) / (x[2] - x[1]), (y[3] - y[2]) / (x[3] - x[2])}; static Real b[n] = { y[0] - k[0] * x[0], y[1] - k[1] * x[1], y[2] - k[2] * x[2]}; int i; // . ? if (X <= x[0]) return y[0]; else if (X >= x[n-1]) return y[n-1]; // . ? for (i = 0; i < n-1; ++i) if (X == x[i]) return y[i]; // . ? for (i = 0; i < n-1; ++i) if (X >= x[i] && X <= x[i + 1]) return k[i] * X + b[i]; return 0; // - !!! } int main (int argc, char *argv[]) { Real y; y = Linear (180); y = Linear (500); y = Linear (1000); y = Linear (6000); y = Linear (10000); y = Linear (30000); y = Linear (0); y = Linear (100000); }
革命的なものもありませんか?
ラグランジュ多項式と線形補間の間には1つの大きな違いがあります。最初のものはポイントの外側に値を明示的に設定できません-それらは計算され、2番目はこの問題を制御できます。 これが、私が線形バージョンに焦点を合わせた理由でもあります。 さらに、私が目指していた対数スケールでは、線形セグメントがより適切なオプションを提供します。
ただし、補間方法については気にしません。 さまざまなメソッドの実装を継承する基本クラスを作成してみましょう
関数を指定/計算するための基本クラス
このクラスは何ができますか? そのようなクラスは次のようにすべきだと私には思えます:
- 引数に応じて関数の値を与える -実際、違いを生むために;
- 補間点の変化に反応(移動および再カウント)する -ある座標で押す/離すという事実が入力に送られ、その結果、パラメーターが再計算されます。
- シングルクリックとダブルクリックを区別するために -私の場合、シングルクリックはポイントの動きを示します。 doubleは新しいポイントを作成します。
- 補間点を移動する場合としない場合の両方で描画します -補間方法が異なると補間点の直感的な値も異なるため、派生クラスはそれらを出力する必要があります(たとえば、補間では、点はグラフの一部です;近似では、点は必然的にグラフ上にあります;ベジェ曲線では、いくつかの点がグラフ上にあり、パーツが形状を設定します);
- 現在の移動点の座標を与える -これは、この点の座標のテキストを表示するために必要です。
- たとえば、「関数は定義されていますか?」、「補間に使用されるポイントの数」、「ポイントの座標を取得する」などのサービス情報を提供します 。これらのデータにより、現在の設定を保存できます。
- 設定 -「できるだけ多くのポイントを配布」、「ポイントの座標を設定」-これにより、保存した設定を復元できます。
まだ考えがありますか? もしそうなら、コメントを書いて、追加してください!
そのようなクラスが判明します:
class FunctorBase { protected: virtual QPointF &get_point (const int Pos) = 0; // virtual QPointF get_point (const int Pos) const = 0; // public: // . virtual void MouseClicked (const QPointF &Pt) = 0; // Pt virtual void MouseDblClicked (const QPointF &Pt) = 0; // Pt virtual void MouseReleased (void) = 0; // virtual void MouseMove (const QPointF &Pt) = 0; // ( ), Pt virtual void DrawPoints (QPainter &p, const ScaleBase &X, const ScaleBase &Y, const int ptRadius, QPen &pnCircle, QBrush &brCircle) = 0; // , virtual void DrawCurPoint (QPainter &p, const ScaleBase &X, const ScaleBase &Y, const int ptRadius, QPen &pnCircle, QBrush &brCircle) = 0; // ( , ) // . virtual qreal f (const qreal t) const = 0; // virtual QPointF *point (void) const = 0; // ; - NULL virtual bool is_specified (void) const = 0; // virtual int num_points (void) const = 0; // QPointF point (const int Num) const; // // . virtual bool set_points (const int Num) = 0; // ; QPointF &point (const int Num); // void set_point (const int Num, const QPointF &Pt); // // . qreal operator() (const qreal t) const { return f(t); } // operator bool (void) const { return is_specified (); } // QPointF &operator[] (const int Num) { return point (Num); } // QPointF operator[] (const int Num) const { return point (Num); } // }; // class FunctorBase inline QPointF &FunctorBase::point (const int Num) { Q_ASSERT_X (Num < num_points (), "receiving points", (QString ("incorrect point index %1 for array size %2 is used"). arg (Num). arg (num_points())).toAscii().constData()); return get_point (Num); } inline QPointF FunctorBase::point (const int Num) const { Q_ASSERT_X (Num < num_points (), "receiving points", (QString ("incorrect point index %1 for array size %2 is used"). arg (Num). arg (num_points())).toAscii().constData()); return get_point (Num); } void FunctorBase::set_point (const int Num, const QPointF &Pt) { point (Num) = Pt; }
(私のスタイルと構造に不満を持っている人のために-客観的に良い提供!)
(コードにエラーを見つけた方へ-ありがとう!)
ここではすべてが明らかだと思います。
座標の場合、ポイントはQPointFの形式で表されます (qreal、qrealの形式の数値のペア。「DoubleはARMを除くすべてのプラットフォームで使用されます」-Qt 4.8で記述されています)。
マウスボタンの
MouseClicked
、
MouseClicked
、
MouseDblClicked
、
MouseReleased
、および
MouseMove
関数で実装されます。 特定の実装では、対応する反応があると想定されています。
ポイントを描画するには、
DrawCurPoint
メソッドと
DrawCurPoint
メソッドが使用されます。 これらを除くすべてのメソッドで抽象座標が使用される場合、ここでは最も画面指向の座標が必要です。 したがって、
ScaleBase
クラスの2つのオブジェクトが変換のためにここに渡されます。 このクラスも仮想です。 彼の祖先は、抽象的な座標から現在の画面への変換を実装しています。 このクラス自体については、以下で説明します。
関数の現在の値は、
f (const qreal)
メソッドとオーバーロードされた演算子関数
operator() (const qreal)
によって返されます。
構造を設定するには、
set_points (Num)
関数を使用します-ポイント数、
point (Num)
、
set_point (Num)
、
get_point (Num)
を設定し、特定のポイントの座標を設定します。
num_points () const
ポイントの数を返します
num_points () const
point (Num) const
、
get_point (Num) const
はポイントの座標を返します。
is_specified () const
は、関数の構造が指定されている場合に
true
返し
true
。
次の記事では、このクラスを実装するためのオプションをいくつか作成します。
垂直/水平スケールの変換機能
線形スケールと対数スケールがあります。 1つの形式で垂直スケールを作成し、別の形式で水平スケールを作成できる場合、チャートには4つのオプションがあります。
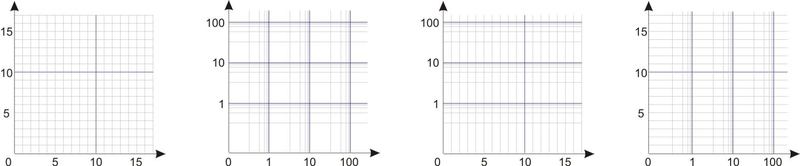
オプション1-両方のスケールは線形です。 オプション2-両方とも対数。 オプション3と4は混合グラフィックです。 ちなみに、私の場合、最終的に出てきたのは混合ケースでした。水平方向には対数目盛、垂直方向-線形が必要だったからです。
したがって、マッピングの問題は両方の軸について個別に解決する必要があります。
画面に表示されるとき、座標への変換が使用されることを思い出してください
これらはどのような機能ですか? 入力では、画面上のコンピューターサブルーチン表示の抽象座標で座標を受け取ります。出力は画面に表示されます(「画面」座標はオペレーティングシステムによって異なります)。計算には、次のことを知る必要があります。

- 抽象座標の限界は 、興味のある引数と関数の限界値です。 なります
、
水平軸と
、
垂直用。 古典的な間違いをする必要はありません:
、
! 上記の例では、これが示されています。
- 画面座標の制限 -グラフが描画される画像の境界。 当然、現在の画面座標で。 グラフで
、
水平軸と
、
垂直用;
- スクリーン座標ステップ -現在のピクセルステップ
、
。 単純なケースでは、ユニットになります。 しかし、Qtでは、垂直方向のゼロはウィンドウの上部です。 だから
。 そして、あらゆる種類の変換を適用することができ、そのステップは決して単一ではありません。
注意してください-変換の問題は、それが垂直軸であるかどうかに関係ありません! それ(タスク)は、入力、出力、および出力パラメーターのステップの境界値で動作します。 したがって、問題は一般化できます。パラメータを変換する必要があります
スケール変換の基本クラス
スケール実装が継承されるスケールの仮想変換クラスの必要な機能を定式化しましょう:
- 画面座標から抽象座標へ、またはその逆への変換 -論理的には、このために行います。
- 変換設定も論理的です。
- プロパティ -現在の変換プロパティ(最小/最大値、異なる値のステップ);
- グリッド情報 -粗いグリッドと細かいグリッドの位置、スケールの下のラベル。
実装は次のようになります。
class ScaleBase { public: // . virtual qreal scr (const qreal Val) const = 0; // virtual qreal val (const qreal Scr) const = 0; // // . virtual const QVector<qreal> &scr_values (void) const = 0; // , [ ( )] int num_scr_values (void) const; virtual const QVector<int> &scr_min_grid (void) const = 0; // int num_scr_min_grid (void) const; virtual const QVector<int> &scr_maj_grid (void) const = 0; // int num_scr_maj_grid (void) const; virtual const QVector<int> &scr_text_pos (void) const = 0; // int num_scr_text_pos (void) const; virtual const QVector<QString> &scr_text_str (void) const = 0; // int num_scr_text_str (void) const; // . virtual qreal val_min (void) const = 0; // , virtual qreal val_max (void) const = 0; // , virtual qreal scr_min (void) const = 0; // virtual qreal scr_max (void) const = 0; // virtual bool is_specified (void) const = 0; // // . virtual void set_val_min (const qreal Val) = 0; // , virtual void set_val_max (const qreal Val) = 0; // , virtual void set_scr_min (const qreal Src) = 0; // virtual void set_scr_max (const qreal Src) = 0; // virtual void set_scr_point (const qreal Src) = 0; // () // . void Resized (const qreal Size) = 0; // // . operator bool (void) const { return is_specified (); } // }; // class ScaleBase int ScaleBase::num_scr_values (void) const { return scr_values().size(); } int ScaleBase::num_scr_min_grid (void) const { return scr_min_grid().size(); } int ScaleBase::num_scr_max_grid (void) const { return scr_max_grid().size(); } int ScaleBase::num_scr_text_str (void) const { return scr_text_str().size(); } int ScaleBase::num_scr_text_pos (void) const { return scr_text_pos().size(); } virtual qreal ScaleBase::scr_step (const int Num) const { Q_ASSERT_X (Num < num_scr_values (), "receiving step", (QString ("incorrect step index %1 for array size %2 is used"). arg (Num). arg (num_scr_values())).toAscii().constData()); return scr_values()[Num + 1] - scr_values()[Num]; }
スケール調整は、
set_... (Val)
関数によって実行さ
set_... (Val)
。 必要な値の再計算は、同じ関数で実行する必要があります。 ウィンドウの
Resized (Size)
が
Resized (Size)
メソッドが
Resized (Size)
ます。
生産性を高めるために、画面上の点と元の抽象的な座標の値の対応を一度計算できます。 この配列は、
scr_values () const
メソッドによって返されます。 さらに、大小のグリッドを作成するために配列が計算されます(関数
scr_maj_grid ()
および
scr_min_grid ()
はそれぞれそれらを返します)。 配列の長さはこれらの行の数に対応し、値は画面上のスケールの先頭からのオフセット(つまり、最初の配列のインデックス)に対応します。 2つの配列も事前に計算されます-スケール上の署名のテキスト(
scr_text_str ()
関数)および開始に対するこれらの署名の変位(
scr_text_pos ()
関数)。
最後に、抽象からスクリーン座標への直接変換は
scr (Val)
関数によって実行され、逆はval
(Scr)
関数によって実行されます。
線形変換
水平軸と垂直軸の別々の線形変換を見てみましょう。

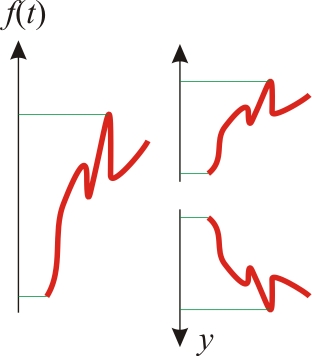
いくつかの機能があります-1つの表現の曲線です。 別の方法として、それを狭くして右に移動する必要がありました(画面上のウィンドウが縮小され、右に移動されました)。 別のビューでは、左に移動する必要がありました(ウィンドウは左に移動しました)。 これは数学的にどのように記述されていますか? 十分簡単:
別のケースでは、曲線の垂直方向の表現を狭めて上に移動する必要がありました。 そして、一般的には裏返します。 これらの変換は両方とも次のように説明されます
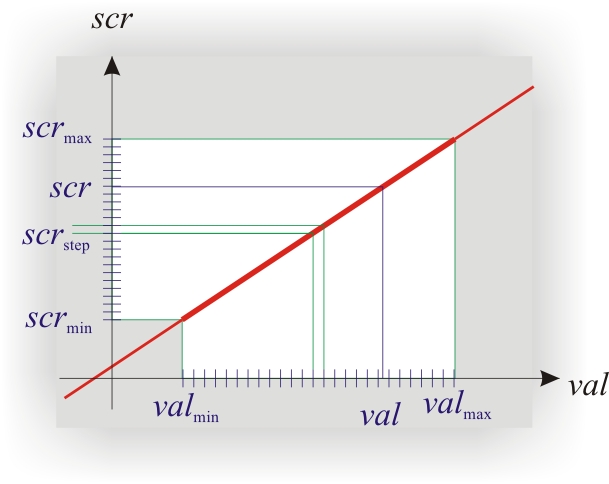
両方の変換の数学的な説明は同じです。
これらの定数の計算は非常に簡単です-これは、2つの方程式のシステムの解決策です。
。
逆変換を実行できることも重要です。たとえば、マウスポインターの座標を抽象的な座標に変換します。 複雑なこともありません:
。
ステップ
これは実際にどのように使用されますか? はい、すべてが簡単です! 水平変換:
対数変換
そして今、私たちはそこに飛び込みます。
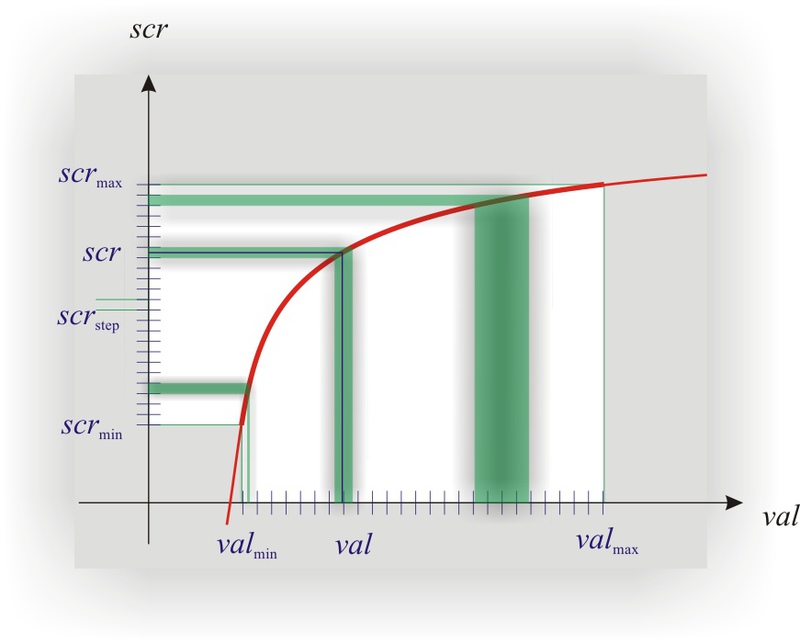
(グラフには対数は描かれていませんが、それに似たものがあります。これは、ここでの対数があまり明確ではないため、意図的に行われます)
もし
合計ポイントがあります
リニアスケール用
私たちはそれを知っています
実際、画面の座標を抽象に変換するアルゴリズム、つまり逆問題がありました。 現在、直接タスクモードは、抽象座標から画面座標に変換することです。 タスクを解決するのは難しくありません。 実際、あなたは見つける必要があります
見つけるために
基本的な数学と考えられているようです。 発見されたエラーや不正確な-コメントを書いて、私は感謝します!
時間が経つにつれて、次の記事を書くことになります-C ++言語のQtツールを使用したこの数学の実装。