理論
理論から始めましょう。最初に、1つの重みの変化が何であるかを思い出します。この場合は正則化ですが、本質は変わりません。
- これ （η）は学習の速度です
- mはトレーニングセットのサイズです
- n-レイヤー番号
- ここに完全な表記
基本的なケースでは、トレーニング速度はすべての重みのグローバルパラメーターです。
各ニューロンの重みごとにトレーニング速度修飾子を導入します
、次のルールに従ってニューロンの重みを変更します。
最初のトレーニングセッションでは、すべてのトレーニング速度修飾子は1に等しく、学習プロセスでの修飾子の動的調整は次のとおりです。
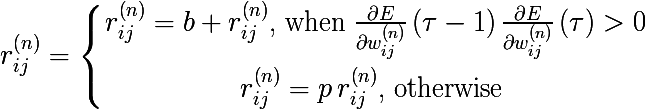
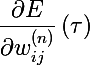-特定の時点での勾配の値 - tauτ-現在の時点または現在のトレーニングバッチ
- b-特定の次元の勾配の方向が変わらない場合に修飾子が受け取る加算ボーナス
- p-勾配ベクトルの方向を変更する場合の乗法的ペナルティ
ボーナスを1未満の非常に小さな数にして、ペナルティを設定するのは理にかなっています
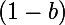、したがってb + p =1。たとえば、a = 0.05、p = 0.95。 この設定により、勾配ベクトルの方向が振動する場合、モディファイア値は初期単位に戻る傾向があります。 数学に進まない場合、アルゴリズムは、前の時点との相対的な方向を保持する重み（重み空間のある次元のフレームワーク内での成長）を促進し、急ぎ始める人に罰金を課すと言えます。
この方法の著者である Geoffrey Hinton （ところで、彼は勾配降下法を使用してニューラルネットワークをトレーニングした最初の人物の1人でもあります）は、次のことを考慮することも推奨しています。
- 最初に、修飾子に適切な成長制限を設定します
- 第二に、この手法をオンライントレーニングや小さなバッチに使用しないでください。 バッチ処理中にかなり一般的な勾配が蓄積することが必要です。 そうでない場合、方向の振動周波数が増加し、それによって修飾子の意味が失われます
実験
すべての実験は、英語の文字が描かれた29 x 29ピクセルの写真のセットで実行されました。 シグモイド活性化機能を備えた100個のニューロンの1つの隠れ層が使用され、 softmax層が出力にあり、クロスエントロピーが最小化されました。 合計すると、ネットワーク内に100 *（29 * 29 + 1）+ 26 *（100 + 1）= 86826の重み（オフセットを含む）があると簡単に計算できます。 重みの初期値は均一な分布から取得されました
。 3つの実験はすべて、同じ重量の初期化を使用しました。 完全バッチも使用されます。
最初に
この実験では、単純で簡単に一般化できるセットを使用しました。 学習速度（グローバル速度）の値は0.01です。 ネットワークエラーの値がトレーニング時代のデータに依存していることを考慮してください。
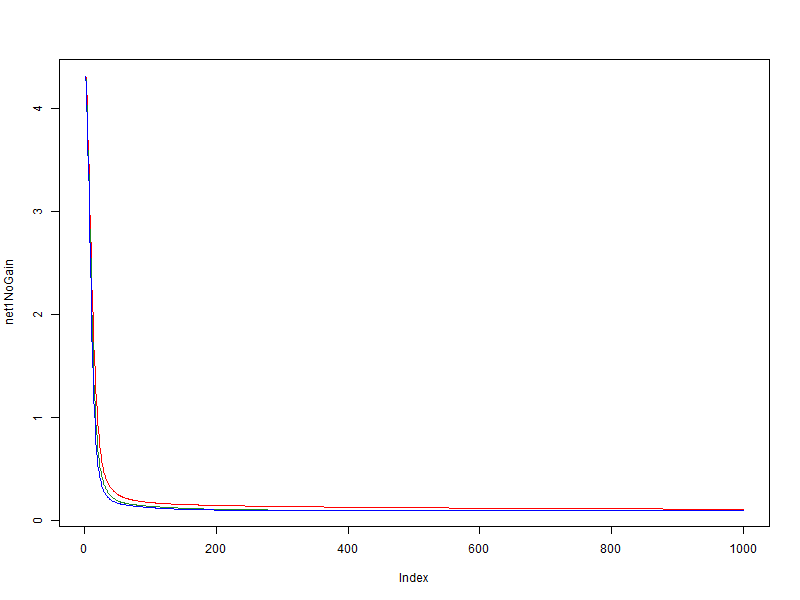
- 赤 -修飾子を使用しない
- 緑 -ボーナス= 0.05、ペナルティ= 0.95、制限= [0.1、10]
- 青 -ボーナス= 0.1、ペナルティ= 0.9、制限= [0.01、100]
非常に単純なセットでは、モディファイアのプラスの効果があることがわかりますが、それは素晴らしいことではありません。
第二
最初の実験とは対照的に、私は多くを取りました。 0.01の学習速度では、誤差関数の値の振動が非常に速く始まり、値が低いほどセットが一般化されることを事前に認識していました。 ただし、このテストでは、正確に0.01が使用されます。 何が起こるか見てみたいです。
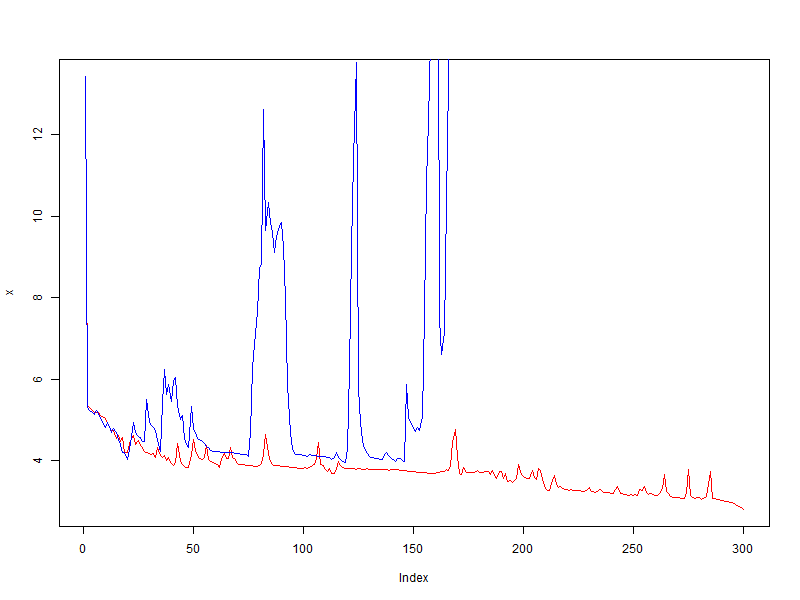
- 赤 -修飾子を使用しない
- 青 -ボーナス= 0.05、ペナルティ= 0.95、制限= [0.1、10]
完全な失敗！ 修飾子は品質を改善しなかっただけでなく、逆に振動を増やしましたが、修飾子がなければ平均でエラーが減少しました。
第三
この実験では、2番目と同じセットを使用しますが、グローバル学習速度は0.001です。
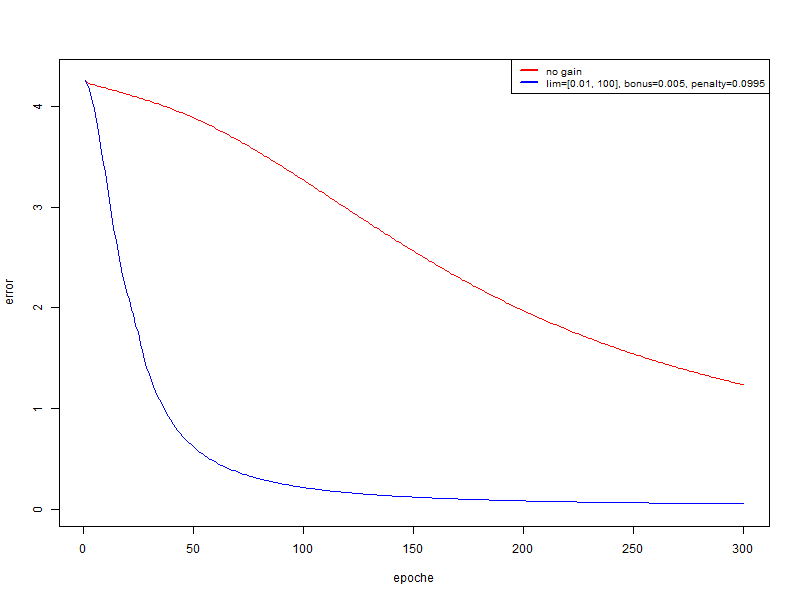
- 赤 -修飾子を使用しない
- 青 -ボーナス= 0.005、ペナルティ= 0.995、制限= [0.01、100]
この場合、品質が大幅に向上します。 そして、300年後、トレーニングセットで認識を引き出してテストする場合：
- 赤 ：トレーニングセット94.74％、テスト67.18％
- 青 ：トレーニングセットで100％; テスト中74.4％
おわりに
そして、私はこの方法がグローバルな学習速度を選択するための代替ではなく、すでに選択されたトレーニング速度への良い追加であると自分自身に結論を出しました。