
なぜこのような単純なタスクの解決策を提示する必要があるのでしょうか? 答えは、合計の階乗を乗算し、階乗の積で除算することで構成される最も単純な方法は、中間計算がuint型やulong型のビットグリッドを超えるため、適切ではありませんが、結果はこれらのタイプの値。 私はこのタスクが好きで、すぐに解決するために座って、3つの方法を思いつきました。 私が他の答えから借りた他の2つの方法。 したがって、この記事では、.NETのC#で実装したすべてのメソッドの説明と比較について説明します。
- 大きな数字
- 表形式
- 二項係数の乗算
- 対数の和と差
- 関数の量と差「階乗の対数」
- 私のやり方
次に、各方法について説明します。
大きな数字
もちろん、最初に思いついたのは、任意の桁数の数字を格納できるBigIntegerの特別なタイプの使用です。 しかし、これは、第一にスポーツではなく、第二に、すべての言語がこれらの型をサポートしているわけではありません(もちろん、自分で書くことができます)が、このメソッドは他のメソッドとは異なり、常に正しい結果を返します丸めます。 ところで、このプロパティを使用すると、他のメソッドの精度をテストできます。これについては後で説明します。
このメソッドのコードは、 uint型の代わりにあらゆる場所にBigIntegerがあることを除いて、単純な実装と違いはありません。 したがって、特に関心はありません。
BigIntegerソース
public static BigInteger BigAr(uint[] numbers) { BigInteger numbersSum = 0; foreach (var number in numbers) numbersSum += number; BigInteger nominator = Factorial(numbersSum); BigInteger denominator = 1; foreach (var number in numbers) denominator *= Factorial(new BigInteger(number)); return nominator / denominator; } public static BigInteger Factorial(BigInteger n) { BigInteger result = 1; for (ulong i = 1; i <= n; i++) result = result * i; return result; }
テーブル方式
これは、Microsoft Excel、 wolframalpha.com、または他のサードパーティのプログラム/サービスで指定された引数からすべての多項係数を計算し、計算された係数をソースコードまたは別のファイルに入力することで構成されます。 このアプローチの欠点は明らかです:高いメモリ消費、引数のすべての許容可能な値からではない係数の計算。 もちろん、この方法のパフォーマンスは最高です。 何らかの方法で、私はこの方法さえ実装していません。
二項係数
この方法は、次の式に従って多項係数の式をいくつかの二項係数の積に分解することで構成されます。
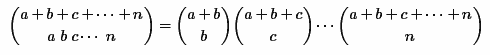
しかし、ここでも、最後の二項係数を計算するときにオーバーフローがすでに発生しています。 これを防ぐために、次の式を使用して各二項係数を再帰的に計算するアルゴリズムが使用されます。
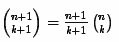
C#コードは次のようになります。
二項ソース
public static ulong BinomAr(uint[] numbers) { if (numbers.Length == 1) return 1; ulong result = 1; uint sum = numbers[0]; for (int i = 1; i < numbers.Length; i++) { sum += numbers[i]; result *= Binominal(sum, numbers[i]); } return result; } public static ulong Binominal(ulong n, ulong k) { ulong r = 1; ulong d; if (k > n) return 0; for (d = 1; d <= k; d++) { r *= n--; r /= d; } return r; }
対数
この方法は、元の式を次のように対数の和と差に分解することで構成されます。
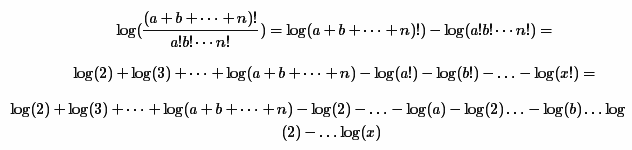
もちろん最後に、 eを結果の程度まで上げる必要があり、それが結果になります。 分子と分母から分母の最大階乗を破棄することからなる小さな最適化も実行されました。 後続の計算を高速化するために、すべての対数がリストにキャッシュされます(この最適化のパフォーマンスは記事の最後でテストされます)。
ログソース
static List<double> Logarithms = new List<double>(); public static ulong Log(params uint[] numbers) { return LogAr(numbers); } public static ulong LogAr(uint[] numbers) { int maxNumber = (int)numbers.Max(); uint numbersSum = 0; foreach (var number in numbers) numbersSum += number; double sum = 0; for (int i = 2; i <= numbersSum; i++) { if (i <= maxNumber) { if (i - 2 >= Logarithms.Count) { var log = Math.Log(i); Logarithms.Add(log); } } else { if (i - 2 < Logarithms.Count) sum += Logarithms[i - 2]; else { var log = Math.Log(i); Logarithms.Add(log); sum += log; } } } var maxNumberFirst = false; foreach (var number in numbers) if (number == maxNumber && !maxNumberFirst) maxNumberFirst = true; else for (int i = 2; i <= number; i++) sum -= Logarithms[i - 2]; return (ulong)Math.Round(Math.Exp(sum)); }
階乗の対数
このメソッドは、階乗対数を対数の合計に分解する代わりに、特別な対数関数がガンマ関数から使用されることを除いて、以前のメソッドとほとんど違いはありません。 実際、他の短い実装(Math.NETなど)がありますが、alglibで実装コードのサイズが最大の場合、実装自体が最も正確であるように思われました。
ログガンマソース
static Dictionary<uint, double> LnFacts = new Dictionary<uint, double>(); public static ulong LogGammaAr(uint[] numbers) { int maxNumber = (int)numbers.Max(); double value; double denom = 0; uint numbersSum = 0; foreach (var number in numbers) { numbersSum += number; if (LnFacts.TryGetValue(number, out value)) denom += value; else { value = LnGamma(number + 1); LnFacts.Add(number, value); denom += value; } } double numer; if (LnFacts.TryGetValue(numbersSum, out value)) numer = value; else { value = LnGamma(numbersSum + 1); LnFacts.Add(numbersSum, value); numer = value; } return (ulong)Math.Round(Math.Exp(numer - denom)); } public static double LnGamma(double x) { double sign = 1; return LnGamma(x, ref sign); } public static double LnGamma(double x, ref double sgngam) { double result = 0; double a = 0; double b = 0; double c = 0; double p = 0; double q = 0; double u = 0; double w = 0; double z = 0; int i = 0; double logpi = 0; double ls2pi = 0; double tmp = 0; sgngam = 0; sgngam = 1; logpi = 1.14472988584940017414; ls2pi = 0.91893853320467274178; if ((double)(x) < (double)(-34.0)) { q = -x; w = LnGamma(q, ref tmp); p = (int)Math.Floor(q); i = (int)Math.Round(p); if (i % 2 == 0) { sgngam = -1; } else { sgngam = 1; } z = q - p; if ((double)(z) > (double)(0.5)) { p = p + 1; z = p - q; } z = q * Math.Sin(Math.PI * z); result = logpi - Math.Log(z) - w; return result; } if ((double)(x) < (double)(13)) { z = 1; p = 0; u = x; while ((double)(u) >= (double)(3)) { p = p - 1; u = x + p; z = z * u; } while ((double)(u) < (double)(2)) { z = z / u; p = p + 1; u = x + p; } if ((double)(z) < (double)(0)) { sgngam = -1; z = -z; } else { sgngam = 1; } if ((double)(u) == (double)(2)) { result = Math.Log(z); return result; } p = p - 2; x = x + p; b = -1378.25152569120859100; b = -38801.6315134637840924 + x * b; b = -331612.992738871184744 + x * b; b = -1162370.97492762307383 + x * b; b = -1721737.00820839662146 + x * b; b = -853555.664245765465627 + x * b; c = 1; c = -351.815701436523470549 + x * c; c = -17064.2106651881159223 + x * c; c = -220528.590553854454839 + x * c; c = -1139334.44367982507207 + x * c; c = -2532523.07177582951285 + x * c; c = -2018891.41433532773231 + x * c; p = x * b / c; result = Math.Log(z) + p; return result; } q = (x - 0.5) * Math.Log(x) - x + ls2pi; if ((double)(x) > (double)(100000000)) { result = q; return result; } p = 1 / (x * x); if ((double)(x) >= (double)(1000.0)) { q = q + ((7.9365079365079365079365 * 0.0001 * p - 2.7777777777777777777778 * 0.001) * p + 0.0833333333333333333333) / x; } else { a = 8.11614167470508450300 * 0.0001; a = -(5.95061904284301438324 * 0.0001) + p * a; a = 7.93650340457716943945 * 0.0001 + p * a; a = -(2.77777777730099687205 * 0.001) + p * a; a = 8.33333333333331927722 * 0.01 + p * a; q = q + a / x; } result = q; return result; }
私の方法
私の方法は、次の操作のシーケンスを適用することです。
- 分母の数の度合いを数えます。 たとえば、引数(5、5、5)の場合、それらはdenomFactorPowers [6] = {0、0、2、2、2、2}になります。 つまり 分母のすべての階乗を乗算すると、3 ^ 2 * 4 ^ 2 * 5 ^ 2 * 6 ^ 2が得られます。 そして度は分子とともに減少し、分子では1 * ... * 15ではなく6 * ... * 15になったため、次数は正確に2番目です。
- 初期化結果= 1 (関数結果); tempDenom = 1 (分母の数値を乗算した結果); currentFactor (分母の現在の係数)。
- 残りのすべての分子番号(maxNumber + 1 ... numbersSum)にわたる変数iのサイクル。
- tempDenom < resultと分母が数値(currentFactor <denomFactorPowers.Length)を 使い果たすまでtempDenomを評価します。
- tempDenom>の結果または数値が分母(currentFactor> = denomFactorPowers.Length)で不足している場合、結果をresult = result / tempDenom * iとして計算します。 この手法により、 result / tempDenom→1であるため、 結果を可能な限り正確にオーバーフローなしで計算できます。
私のメソッドソース
public static ulong MyAr(uint[] numbers) { uint numbersSum = 0; foreach (var number in numbers) numbersSum += number; uint maxNumber = numbers.Max(); var denomFactorPowers = new uint[maxNumber + 1]; foreach (var number in numbers) for (int i = 2; i <= number; i++) denomFactorPowers[i]++; for (int i = 2; i < denomFactorPowers.Length; i++) denomFactorPowers[i]--; // reduce with nominator; uint currentFactor = 2; uint currentPower = 1; double result = 1; for (uint i = maxNumber + 1; i <= numbersSum; i++) { uint tempDenom = 1; while (tempDenom < result && currentFactor < denomFactorPowers.Length) { if (currentPower > denomFactorPowers[currentFactor]) { currentFactor++; currentPower = 1; } else { tempDenom *= currentFactor; currentPower++; } } result = result / tempDenom * i; } return (ulong)Math.Round(result); }
テスト中
すべてのメソッドのテストは2段階で行われました。これは、オーバーフローおよび丸めエラーのない任意のメソッドで計算できる最大数のテストと、速度テストです。
計算可能な最大数のテスト
多項係数が可換演算であることを証明するのは簡単です。 例:M(a、b、c)= M(a、c、b)= M(c、b、a)など そのため、指定された数の引数を持つ数値のすべての組み合わせを確認するには、繰り返しのある順列を使用できます。 これらの目的のため、ライブラリを使用してcodeprojectからデータおよびその他の組み合わせを生成しました 。 したがって、すべての組み合わせは辞書編集順に並べられました。
以下の2つのグラフは、多項関数の引数の数に対する可能な最大の計算可能な数の置換数の依存性を示しています。
理解を深めるために、2つの引数を持つ値の最初のセットについて説明します。
Arg count: 2 Naive(1,19) = 20; #18; overflow Binom(1,61) = 62; #60; overflow LogGamma(5,623) = 801096582000; #4612; rounding(error = 1) Log(6,588) = 59481941558292; #5572; rounding(error = 1) My(7,503) = 1708447057008120; #6481; rounding(error = 1) Big(8,959) = 18419736117819661560; #7930
上記のテストでは、たとえば、対数を使用して計算できる最大のulong値は59481941558292です。これは、引数6および588から計算されたもので、辞書順で生成した場合の置換6481に対応します。 この数値は緑のグラフに表示されます。 丸めという用語は、次の順列、つまり (6.589)、このメソッドは1の誤差を持つ多項係数を考慮します。また、 オーバーフローという用語は、次の順列から係数を計算する場合(たとえば、 Binomに対して(1.63)を使用する場合 )、メソッド内のどこかでオーバーフローが発生することを意味します。
最初と最後の置換数の差が大きすぎるため、グラフを2つの部分に分割します(引数の数は2-10と11-20)。 21個以上の引数では、すべての関数は最初の順列でも誤った結果を返します(これは、Multinomial(1,1、...、1)= 21!であり、この数は最大ulongより大きいため、 理解できます)結果を増やすだけです。この声明は証拠なしのままにしておきます)。
オレンジのグラフは完璧な結果を示しています。 一般に、引数の数が指定された多項関数によってのみ計算できる最も長いulong 。 つまり 順列をさらに増やすと、結果はulong型を超えます。 このグラフの値は、記事の冒頭で説明した大きな整数を使用して計算されました。
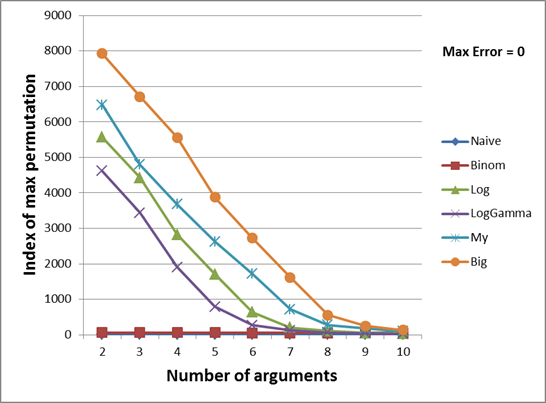
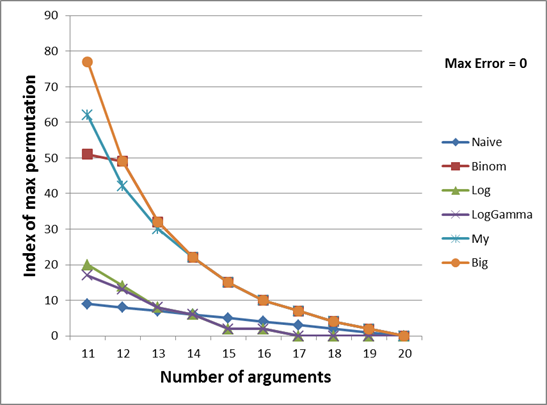
したがって、両方のグラフからわかるように、私の方法では、12個と13個の引数を除いて、ほとんどすべての場合でより大きな係数を計算できます。 二項係数への期待は高いものの、小さな数(2から8)の場合には小さな値のセットをカバーすることが判明しました。 9からはLogおよびLogGammaよりも広い範囲に広がり始め 、12および13からは私のメソッドをバイパスします。 ただし、私の方法で計算されるため、13以降は完全に計算されます。
Log メソッドとLogGammaメソッドは 、特に多数の引数がある場合、ほぼ同じ範囲をカバーします。 LogがLogGammaよりも1〜12先行しているという事実は、おそらくLog(N!)関数が実数(対数)の合計よりも正確に計算されないためです。 また、15〜19個の引数については、単純な方法でも対数よりも効果的であることが判明しました。
Max Errorの絶対誤差(つまり、丸め中の最大許容誤差)が変わっても画像はあまり変わらなかったことに注意する価値があります。そのため、 Max Errorが10および100の他のグラフは示しませんでした。
メソッド性能テスト
各メソッドの速度を測定するために、2つのテストセットを使用しました。 最初の例は非常に大きな数値を対象としているため、単純なNaiveメソッドはオーバーフローエラーでクラッシュするため、考慮されませんでした。 BigIntegerもカウントされませんでした。 各セットを20,000回実行し、この計算時間を測定しました。
また、これらのメソッドはprefetchありとなしでテストされています。 これは、事前に計算された対数と階乗からの対数のみを使用するため、 LogおよびLogGammaメソッドにのみ関連します。
引数の最初のテストセット
(1, 1) (1, 2) (2, 1) (2, 2) (5, 5, 5) (10, 10, 10) (5, 10, 15) (6, 6, 6, 6) (5, 6, 7, 8) (2, 3, 4, 5, 7)

ご覧のとおり、ここでの私の方法は他の方法よりも3倍悪いことがわかりました。
Binomが他の誰よりも速くすべてを計算したという事実は、整数演算のみを使用するという事実によって説明されます。これはアプリオリにより高速です。
LogGammaのLogに対するわずかなリードは、対数を再び加算しないが、階乗の対数をすぐに覚えているという事実によって説明されます。 たとえば、Ln(2)+ Ln(3)+ Ln(4)の代わりに、Ln(4!)が使用されます。
また、プリフェッチが判明したように、実際にはLogおよびLogGammaの速度に影響を与えず、これらの関数の計算がすでに計算された値の抽出に明らかに匹敵すること、または計算時間が合計に比べて短すぎることを示唆しています残りの操作の時間。
引数の2番目のテストセット
次のセットは、最も単純な単純な機能でさえ意図されていました。 次の図には、より大きな数字も含まれています。
(1, 1) (1, 2) (2, 1) (2, 2) (5, 5, 5) (1, 1, 1, 1, 1, 1, 1, 1, 2) (1, 2, 3, 4, 5, 4)

ご覧のとおり、この場合、私のメソッドは他の関数( Bigを除く)とのギャップが小さく、大きな数のメソッドは私のメソッドよりも4倍悪いことがわかりました。 これは、.NETでの多数の実装が理想からほど遠いためです。 System.NumericsライブラリのいくつかのメソッドをILSpyで逆コンパイルすると、私の仮定が確認されました(コードは、加算などの単純な操作でも、大量の安全なコードが使用されることを示しています)。
.NETでのBigIntegerの操作の追加
public static BigInteger operator +(BigInteger left, BigInteger right) { if (right.IsZero) { return left; } if (left.IsZero) { return right; } int num = 1; int num2 = 1; BigIntegerBuilder bigIntegerBuilder = new BigIntegerBuilder(left, ref num); BigIntegerBuilder bigIntegerBuilder2 = new BigIntegerBuilder(right, ref num2); if (num == num2) { bigIntegerBuilder.Add(ref bigIntegerBuilder2); } else { bigIntegerBuilder.Sub(ref num, ref bigIntegerBuilder2); } return bigIntegerBuilder.GetInteger(num); } ... public void Add(ref BigIntegerBuilder reg) { if (reg._iuLast == 0) { this.Add(reg._uSmall); return; } if (this._iuLast != 0) { this.EnsureWritable(Math.Max(this._iuLast, reg._iuLast) + 1, 1); int num = reg._iuLast + 1; if (this._iuLast < reg._iuLast) { num = this._iuLast + 1; Array.Copy(reg._rgu, this._iuLast + 1, this._rgu, this._iuLast + 1, reg._iuLast - this._iuLast); this._iuLast = reg._iuLast; } uint num2 = 0u; for (int i = 0; i < num; i++) { num2 = BigIntegerBuilder.AddCarry(ref this._rgu[i], reg._rgu[i], num2); } if (num2 != 0u) { this.ApplyCarry(num); } return; } uint uSmall = this._uSmall; if (uSmall == 0u) { this = new BigIntegerBuilder(ref reg); return; } this.Load(ref reg, 1); this.Add(uSmall); }
おわりに
実験により、私の計算方法は、計算可能な最大数のコンテキストでは他のメソッドよりも優れていることがわかりました(ただし、理想的なものよりもさらに劣っています)が、パフォーマンスのコンテキストでは劣っています(同時に、.NETでの多数の実装よりもはるかに優れています)。 また、.NETでの大きな数の算術の実装は理想からはほど遠いものであり、それを別のメソッドに置き換えることができる場合は、それを使用することをお勧めします。
二項係数を使用した方法は、単純な実装よりも高速で、さらに高速であることが判明しましたが、整数演算のみを使用するため、これは非常に明白です。 一方、このメソッドは、特に少数の引数の場合、広範囲の値をカバーしません。
また、実験では、階乗の対数と対数の計算値を再利用してもパフォーマンスが大幅に向上しないため、それらを省略できることが示されました。
この実験で行われた作業が私にとってだけでなく興味深いものになることを願っています。そのため、ソースコードと単体テストおよびgithubのテスト: Multinimonal-Coefficientを投稿します。
更新