
友人たち、私は相対性理論の特別な理論の理解に潜り続けることを提案します。
すでに写真、アニメーション( ここ )、思考実験のコンピューターシミュレーション( ここ )もありましたが、SRTを揺るがすことはできませんでした。 ほとんどのパラドックスは、綿密な調査の結果、論理的な説明が見つかりました。 後者を解決するために残っており、最も簡単な...
新年、そして今のところいつものように、私の友人と私は新しいパラドックスとSRTの反論を思い付き/解決します...来る2017年に、私は言葉遣いに関して最後で最も単純なパラドックスを解決することを提案します。
光の速度で正確に移動するオブジェクトのパラドックス:
質問は非常に簡単に提示できます。
-SRTの観点からの光子とは何ですか? それは特別な相対性理論の観点からであり、他の理論ではありません。
現代の物理学では、光の速度(たとえば、単一光子)で正確に動く粒子の存在が実験的に証明されています。
光子が現実に存在し、粒子の特性を持ち、光の速度で移動するという事実は、すべてのIRFでの光の速度の不変性の仮説に反論します。 なぜなら 静止している光子のIRFに対して、その速度はゼロであり、光子は軽いです。
多くの人は、光子が量子場の理論などで考慮されるべきであるという事実によってこの事実についてコメントしました。 同様の理論。 ただし、STOの定式化では、適用できる物理オブジェクトに制限はなく、宇宙に物理的に存在する1つのオブジェクトだけにそれを正しく適用できない場合、これは完全に反論します。
2017年1月21日現在の更新。
別の新年サービスパラドックス(弾丸とワゴン)にソリューションを追加しました
1.車の先頭(ポイントA)にシューティングゲームがあり、車の中央(テーブルB)にテーブルがあり、車の末尾(ポイントB)にターゲットがハングしているとします。 これらの各ポイントには、車の時刻に同期したクロックがあります。
(ワゴンの終わり)--------------------(ワゴンの始まり)
(ポイントB)----------(ポイントB)----------(ポイントA)
2.時刻t = -10に、射手がターゲットの方向(ポイントA)に弾丸を発射し、時刻t = 0の車の時計により、弾丸が車の中央(ポイントB)にあり、時刻t = + 10ヒットターゲット(ポイントB)
(ワゴンの終わり)--------------------(ワゴンの始まり)
(ポイントB)----------(ポイントB)----------(ポイントA)
(t = + 10)-------------(t = 0)--------------(t = -10)
<<< ----------------------------------------(箇条書き)
つまり、弾丸は(ポイントA)から(ポイントB)に移動します
3.今、私たちの車が、駅の観測者の視点から、弾丸の飛行とは反対の方向に相対論的速度で動くと想像してください。
(ポイントB)----------(ポイントB)----------(ポイントA)
<<< ----------------------------------------(箇条書き)
(電車)-------------------------------------- >>>
4.車の反対側にあるステーションに、ポイントA、B、C-NA、NB、HBのちょうど反対側に3人の観測者がいるように一致させます。
(ワゴンの終わり)--------------------(ワゴンの始まり)
(ポイントB)----------(ポイントB)----------(ポイントA)
(t = + 10)-------------(t = 0)--------------(t = -10)
(HBポイント)-------(NBポイント)-------(HAポイント)
(tn = 0)-------------(tn = 0)--------------(tn = 0)
5. NA、NB、NVのすべてのオブザーバーのクロックは、ステーションの時刻に従って同期され、同時に3つがアラームtn = 0により、対応するポイントA、B、Bで通過する車の窓を覗き込みます。
6.そして、wiki( https://ru.wikipedia.org/wiki/Special_theory_of relativity(セクション:4.3同時性の相対性理論))で説明されているように、すべてが一致するようにします。
-中央オブザーバー(ポイントNB)-(ポイントB)車の時計でt = 0を確認し、それに応じてそこのテーブルを弾丸が飛んでいます。
-右側の観測者は車の始まりを見る(ポイントON)-(ポイントA)t = -10の時計と弾丸、武器から飛び出すガンマン
-左のオブザーバーは車の終わりに見えます(HBポイント)-(ポイントB)t = 10の時計とターゲットに当たる弾丸
7.つまり 3人の観測者が車の中で同時に視線を合わせると、反対側に同じ弾丸が見えます。 これは同時性の相対性の原理であり、同時に駅で起こること-車に乗っている人の観点からは、同時に起こることはありません。
説明しましょう:
車内のオブザーバーの観点からは、すべてが次のようになりました。
-サービスステーションに応じて、キャリッジが静止してステーションが移動しているため、ステーションのサイズが小さくなります(キャリッジよりも小さくなります)。
-観測者は最初に(ポイントON)のウィンドウを見る-(ポイントA)クロックがt = -10であり、矢印が弾丸を発している
-この後のみ、2番目の観測者は(ポイントNB)のウィンドウを見る-(ポイントB)t = 0の時計とテーブル上を飛んでいる弾丸を見る
-その後、3人目の観測者は(HBポイント)-(ポイントB)の窓を覗き込み、t = 10の時計と弾丸が標的に当たるのを確認します。
8.矛盾はないように思えますが、矛盾はありません。
-観測点を(点NB)-(点B)のステーションにパンに追加しましょう。
-その後、列車の窓の外を見てフライパンを代用すると、彼は弾丸をターゲットに飛ばせません。
-したがって、(ポイントHB)-(ポイントB)のオブザーバーは、弾丸がターゲットにどのように当たるかがわかりません。
-逆に、(ポイントNB)-(ポイントB)のオブザーバーがパンを置き換えないことを決定した場合、(ポイントHB)-(ポイントC)のオブザーバーは、弾丸がターゲットにどのように当たるかを確実に確認できます。
9.これはそうだと思われますか?
しかし、SRTの矛盾が現れるのはまさにここです-少しの情報(弾丸がターゲットにヒット/ミスしました)がオブザーバーから(ポイントNB)に送信されます-(ポイントB)-(ポイントHB)-(ポイントC)-即座に(ポイントから)ステーションビュー)。
つまり 情報転送速度は距離に依存しません(車の長さを任意に変更し、観測所を駅の適切な地点に配置できます)。 国立図書館と国会の各地点にいる観測者は、(駅の時間に応じて)同時に情報を送受信します(国立図書館0/1からの信号は直ちに国立図書館に送信されます)
そして、これはサービスステーションとはまったく逆です。
間違いは、プラットフォームの3人の観測者が、列車の始点、中点、終点を同時に見て、同じ弾丸を見るという主張にあります。 はい、彼らはそれぞれ、車のシューターの視点から「未来」を見ますが、この「未来」では彼らが見た場所で-弾丸はまだ存在しません。 そして一般的に、射手と彼の反対側のプラットホームにいる観察者を除いて、射撃の時点で、誰も弾丸を見ることができません。
これは逆説的な状況です。無限の数の観測者をプラットフォーム上に最短距離で配置し、全員が列車でのショットの瞬間を見ると、列車の矢印の反対側にのみ弾丸が表示され、他の人は車の「未来」を見ることができます、しかし、「未来の馬車」のこれらの無限の観測ポイントのいずれにも弾丸はありません。
これはサービスステーションで許可されており、無限の数のオブザーバーのそれぞれは、空間の特定の時点で特定の時間に自動車の「未来」のみを参照し、これらのオブザーバーはすべて一緒に自動車の「完全な未来」(つまり、空間と時間のすべてのポイント)。 つまり シューターの右側のプラットホームにいるすべてのオブザーバーは、ショットの時点で、弾丸がまだ存在しない「未来の一部」の車のみを見ることができます。

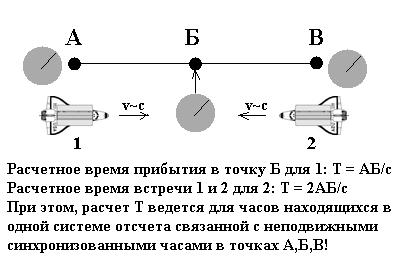
, , . , , .
. .
, , , 2 . ( )
, .
1
, .
2
C .
( , , 2 ( ), 1 ( ). .. C=const , C+V=C)
« »:
, , , () .
:
, ( , , t ), , …
, , :
« , , , , .. , ».
– . , , , .

:
1. ( C, 0). -, .
2. - , , T=/.
3. , . - . 2 , 1) , T ( , - ), , (.. T, T).
4. « », -, « ?». , , , ! , - , , , ( ), «» ( ). - , , , .
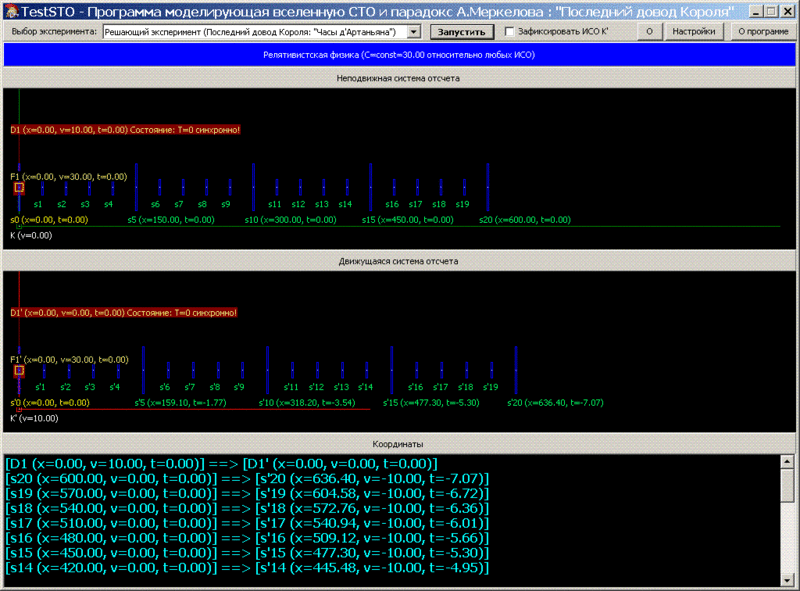
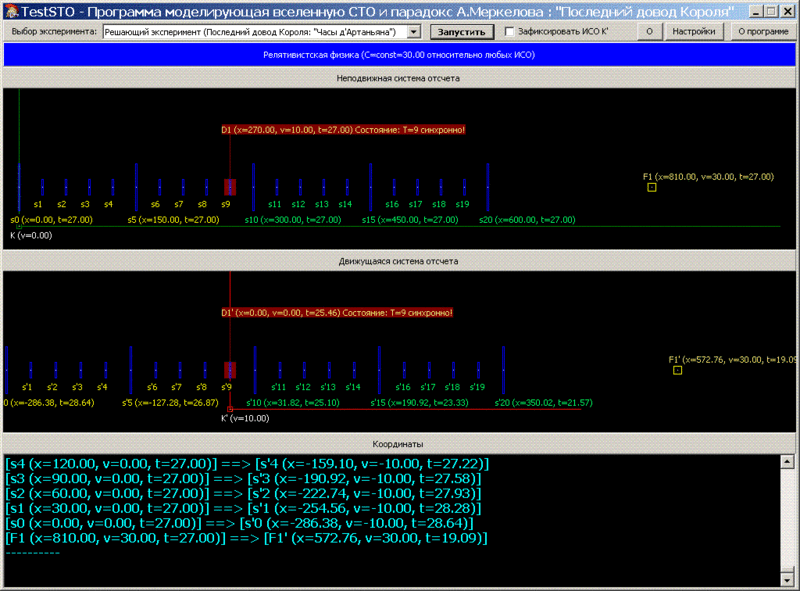
, -, . - , , , , .
, , , . ’ -: « - , , ?». , , C+C<>2C, C+C=C, : « ». «», ’, :
1. , , T = / , . T=/C. , , , , , .. , .
2. , , , (.. ) T = / , = =+=2, C+C C, . T=2/. , , , , .
3. , ( ) . T=/C T=2/C, .. /C = 2/C. , ! 1 , .
4. , , , , .
:
— , , , , — , — , . . .. - , ( ).
:
, – , , , . , , , , . () , , , , , . , . , , 12 ( ), , , () . , «» , lib.rus.ec/b/300909/read ( ), , , , .
, , :
1 , 2 , ( ) , . , .. ( ). ? , , 1 ?
:
3 , , . , ( 6:00 ) . . .. , , , .
, , , , ( ):
1.
2.
3. , =/
4.
5.
6. , +-1, T=2/ >> T=/
, , - , .
T = / ( 5 ), = =+=2, C+C C (.. C+C=2C), . T=2/
T=2/ >> T=/ :
T = /
1…
= , = +0 ( )
2. 2 (, , ! , )
= =+=2, C+C C (.. C+C=2C), . T=2/
T=2/ >> T=/!
= + = 2C, 2:
C .
( , , 2 ( ), 1 ( ). .. C=const , C+V=C) C.
— 1/ :) — :
— . /, , . =/=/=2/2.
1. , , .
2. ?( , )
T = / . (.. )
:
= =+=2, C+C C (.. C+C=2C), . T=2/, 2, , T = 2A/(C+C) = 2/2 = AB/C ( 1 ),
, C+C=2C, C+C=C.
:
, - , 2 2 2 , - 2 .
, C+C=2C ( , = 2 ( , )) 1C, ...
, , <= 2, , 2, .. — , . :
() = 2C, , , 2 2. : = v1+v2, v2 = — v1, .. 1 v1=0, v2( 2 ) = — 0, .. v2 = 2C — 0 = 2C! .. , = 2C — 2. , , 1 2 ( ), …
(V12) = (V1+V2) / (1 + (V1*V2)/C^2), V2, V2 = (V12 *^2 — V1*C^2) / (C^2 — V12*V1)
: (V12) = 2, V1=0
V2 = (2C*C^2 — 0*C^2) / (C^2 — 2C*0) = (2C*C^2) / C^2 = 2C! . .. , = 2C — 2
弾丸とワゴンの逆説:
1.車の先頭(ポイントA)にシューティングゲームがあり、車の中央(テーブルB)にテーブルがあり、車の末尾(ポイントB)にターゲットがハングしているとします。 これらの各ポイントには、車の時刻に同期したクロックがあります。
(ワゴンの終わり)--------------------(ワゴンの始まり)
(ポイントB)----------(ポイントB)----------(ポイントA)
2.時刻t = -10に、射手がターゲットの方向(ポイントA)に弾丸を発射し、時刻t = 0の車の時計により、弾丸が車の中央(ポイントB)にあり、時刻t = + 10ヒットターゲット(ポイントB)
(ワゴンの終わり)--------------------(ワゴンの始まり)
(ポイントB)----------(ポイントB)----------(ポイントA)
(t = + 10)-------------(t = 0)--------------(t = -10)
<<< ----------------------------------------(箇条書き)
つまり、弾丸は(ポイントA)から(ポイントB)に移動します
3.今、私たちの車が、駅の観測者の視点から、弾丸の飛行とは反対の方向に相対論的速度で動くと想像してください。
(ポイントB)----------(ポイントB)----------(ポイントA)
<<< ----------------------------------------(箇条書き)
(電車)-------------------------------------- >>>
4.車の反対側にあるステーションに、ポイントA、B、C-NA、NB、HBのちょうど反対側に3人の観測者がいるように一致させます。
(ワゴンの終わり)--------------------(ワゴンの始まり)
(ポイントB)----------(ポイントB)----------(ポイントA)
(t = + 10)-------------(t = 0)--------------(t = -10)
(HBポイント)-------(NBポイント)-------(HAポイント)
(tn = 0)-------------(tn = 0)--------------(tn = 0)
5. NA、NB、NVのすべてのオブザーバーのクロックは、ステーションの時刻に従って同期され、同時に3つがアラームtn = 0により、対応するポイントA、B、Bで通過する車の窓を覗き込みます。
6.そして、wiki( https://ru.wikipedia.org/wiki/Special_theory_of relativity(セクション:4.3同時性の相対性理論))で説明されているように、すべてが一致するようにします。
-中央オブザーバー(ポイントNB)-(ポイントB)車の時計でt = 0を確認し、それに応じてそこのテーブルを弾丸が飛んでいます。
-右側の観測者は車の始まりを見る(ポイントON)-(ポイントA)t = -10の時計と弾丸、武器から飛び出すガンマン
-左のオブザーバーは車の終わりに見えます(HBポイント)-(ポイントB)t = 10の時計とターゲットに当たる弾丸
7.つまり 3人の観測者が車の中で同時に視線を合わせると、反対側に同じ弾丸が見えます。 これは同時性の相対性の原理であり、同時に駅で起こること-車に乗っている人の観点からは、同時に起こることはありません。
説明しましょう:
車内のオブザーバーの観点からは、すべてが次のようになりました。
-サービスステーションに応じて、キャリッジが静止してステーションが移動しているため、ステーションのサイズが小さくなります(キャリッジよりも小さくなります)。
-観測者は最初に(ポイントON)のウィンドウを見る-(ポイントA)クロックがt = -10であり、矢印が弾丸を発している
-この後のみ、2番目の観測者は(ポイントNB)のウィンドウを見る-(ポイントB)t = 0の時計とテーブル上を飛んでいる弾丸を見る
-その後、3人目の観測者は(HBポイント)-(ポイントB)の窓を覗き込み、t = 10の時計と弾丸が標的に当たるのを確認します。
8.矛盾はないように思えますが、矛盾はありません。
-観測点を(点NB)-(点B)のステーションにパンに追加しましょう。
-その後、列車の窓の外を見てフライパンを代用すると、彼は弾丸をターゲットに飛ばせません。
-したがって、(ポイントHB)-(ポイントB)のオブザーバーは、弾丸がターゲットにどのように当たるかがわかりません。
-逆に、(ポイントNB)-(ポイントB)のオブザーバーがパンを置き換えないことを決定した場合、(ポイントHB)-(ポイントC)のオブザーバーは、弾丸がターゲットにどのように当たるかを確実に確認できます。
9.これはそうだと思われますか?
しかし、SRTの矛盾が現れるのはまさにここです-少しの情報(弾丸がターゲットにヒット/ミスしました)がオブザーバーから(ポイントNB)に送信されます-(ポイントB)-(ポイントHB)-(ポイントC)-即座に(ポイントから)ステーションビュー)。
つまり 情報転送速度は距離に依存しません(車の長さを任意に変更し、観測所を駅の適切な地点に配置できます)。 国立図書館と国会の各地点にいる観測者は、(駅の時間に応じて)同時に情報を送受信します(国立図書館0/1からの信号は直ちに国立図書館に送信されます)
そして、これはサービスステーションとはまったく逆です。
パラドックスソリューション:
間違いは、プラットフォームの3人の観測者が、列車の始点、中点、終点を同時に見て、同じ弾丸を見るという主張にあります。 はい、彼らはそれぞれ、車のシューターの視点から「未来」を見ますが、この「未来」では彼らが見た場所で-弾丸はまだ存在しません。 そして一般的に、射手と彼の反対側のプラットホームにいる観察者を除いて、射撃の時点で、誰も弾丸を見ることができません。
これは逆説的な状況です。無限の数の観測者をプラットフォーム上に最短距離で配置し、全員が列車でのショットの瞬間を見ると、列車の矢印の反対側にのみ弾丸が表示され、他の人は車の「未来」を見ることができます、しかし、「未来の馬車」のこれらの無限の観測ポイントのいずれにも弾丸はありません。
これはサービスステーションで許可されており、無限の数のオブザーバーのそれぞれは、空間の特定の時点で特定の時間に自動車の「未来」のみを参照し、これらのオブザーバーはすべて一緒に自動車の「完全な未来」(つまり、空間と時間のすべてのポイント)。 つまり シューターの右側のプラットホームにいるすべてのオブザーバーは、ショットの時点で、弾丸がまだ存在しない「未来の一部」の車のみを見ることができます。
2014年6月7日の更新
x ------- x
2014年6月7日の更新
ホスポダ、この投稿に対する最後のコメントから1年以上が経過したことをお知らせします。これについてもあなたは満足していると思います:)
議論の各当事者は納得がいかないままでしたが、それでも...同意しますが、議論するのは面白かったです;)
しかし...時間が経ち、もちろん私たち全員は真面目で忙しい人です...したがって、貴重な数秒を無駄にしないように、最近思いついた2分間の実験を見ることをお勧めします。
そして、表示後、相対性理論を擁護する議論があれば、少し議論することができます。
x ------- x
この記事の内容を理解するためには、ステレオタイプのない明確な頭を持つ必要があります。 したがって、まずは、同僚を楽しませるために5年ほど前に思いついた1つの簡単な問題を解決して、神経系を活性化することをお勧めします。
球の中には、そこから引き出す必要のある特定のオブジェクトがあります。 問題は抽象的であるため、物理法則に拘束されず、任意の方法を使用して解決できます。1つの条件があります-このオブジェクトは球を通過できず、球を破壊できません。
簡略化:
ゴム製のボールの内側には小石があり、引き抜く必要がありますが、ボールをナイフで刺したり、チェーンソーで挽いたりすることはできません。
私はこの問題を解決するための4つのオプションを考え出しました(たぶんもっと見つけるでしょう):
畳み込みを動かして喜んでいただけたことを願っています。今、私たちは最も興味深いものに目を向けています。
証明のキーポイント:
1. SRTで使用されるローレンツ変換には、クロノスピードを正しく計算するための基準はありません。
1.1。 同じISOの計算方法が異なると、速度も異なります。
1.2。 クロノ速度の物理的意味を説明し(ダルタニャンによるクロノ速度の測定の例を使用)、実際には(SRTが説明しているように)ローレンツ変換を使用した計算で得られるのはSUCHではないかもしれないことを示すために。
1.3。 クロノシフトに関する情報のないローレンツ変換は、クロノスピードの正しい計算ができないことを示すため。
証明:
私の理由は次のとおりです。
この段落の目的は、クロノスピードの論理的/物理的意味を示すことです。
最大の仕事は、「クロノスピード」という言葉の私の論理的な説明の後、あなた自身がそれを測定する方法の結論に達することです。
最小のタスクは、例として時間間隔の測定/計算を行う方法が正しいことに同意することです。
それでは始めましょう。
クロノスピードの意味を理解するには、2つのイベント間の時間(時間間隔)を測定する方法に同意する必要があります。
次の2つのオプションがあります。
1)両方のイベントは空間の1つのポイントで発生します
2)イベントは空間のさまざまなポイントで発生します
時間間隔では、通常の時間だけでなく、2つのイベントの間に行うダルタニャンスクワットの数を測定します。 一見、これは余分な重複のように思われるかもしれませんが、後で示すように、ダルタニャンの導入は基本的に理解するためのものです。 あなたの目を開くのはそれです。
1)タイムラプス測定手順
両方のイベントが空間の1つのポイントで発生する場合
-イベントが行われる時点で数時間あります
-時計はダルタニャンです
-event1の時点で、クロックt = 0、d'Artagnanがしゃがみ始め、しゃがんだ数k = 0
-クロックt = Tのevent2の時点で、ダルタニャンはしゃがむのをやめk = K
-結果:測定された期間は、時間ごとにT、ダルタニャンごとにKです。
2)タイムラプス測定手順
空間のさまざまなポイントでイベントが発生する場合
-d'Artagnansを使用したCh1とCh2のクロックは、event1とevent2のポイントに配置されます(クロックは互いに相対的に静止しています)
-クロックCh1とCh2はアインシュタイン法によって同期され、その後永久に同期します(ISO Ch1 / Ch2で)
-11 t = 0のpoint1のevent1の瞬間、d'Artagnanはスクワットを開始しますk = 0
-22 t = Tのpoint2のevent2の時点
-Ch2は、このデータ(t = T)を含むSMSを、まだしゃがんでいるCh1のd'Artagnanに送信します。 (SMSは重要ではありません。信号または伝書鳩の場合があります。測定に影響しないため、重要ではありません)
-Chs1でsmsku d'Artagnanを受け取った人は、しゃがむのをやめ、彼の日記を調べます。 ダルタニャンがしゃがむと、彼らはスクワット雑誌を保管していることがわかります:)。 この雑誌には、「時間」と「すでに完了したスクワットの数」という2つのコラムしかありませんが、時間Tで、Ch1のd'ArtagnanがKスクワットを完了したことがわかりました。
-結果:測定された期間は、時間ごとにT、ダルタニャンごとにKです。
もっと...
これで、1つのポイントでの2つのイベント(1)と異なるポイントでの2つのイベント(2)の時間間隔を測定できます。
測定された期間の物理的な意味は、 d'Artagnanがevent1とevent2の間に実行することができたスクワットの数と見なします。
これは重要ではありません-どのようにして、1mまたは2mの期間を測定しても、これからのスクワット数は変わりません。
1つのISOで測定される時間間隔は、その測定方法に依存しないことを証明しましょう((1)または(2)):
P1 / P2-同期して、つまり 同じ読み値t = Tを同時に表示します。 もちろん、ISO Ch1 / Ch2に関しては。
Ch2でTを思い出すと、Ch1で同時にそれを断言できます。 同じ瞬間t = T つまり 同期クロックの読み取り値は、それらの間の距離に依存しません(1つのISOで)。 つまり 実際、ISO Ch1 / Ch2で時間間隔を測定したのは1時間Ch1だけでした。 測定の完了の瞬間は、Ch2の同期稼働時間によって行われました。Ch2の読み取り値は、Ch1の読み取り値とまったく同じです(ISO Ch1 / Ch2で)。
「イベントの期間」の概念を定義します。
イベントABの期間は、1つのISOで測定されたイベントAとイベントBの間の期間です。
これで、クロノスピードの概念を紹介できます。
CHRONIC SPEED(H)は、ISOごとにONEおよびSAMEイベントのDURATIONが何回異なるかを示す係数です。
ISO2に対するISO1速度は、ISO1のevent1とevent2の間で測定された時間間隔と、ISO 2のTEM SAME event1とevent2の間で測定された時間間隔の比率です。
クロノ速度の実験的測定の場合 -ISO1ではh1(T1)時間、ISO2ではh2(T2)時間のONEおよびSAMEイベントの継続時間を測定するだけで十分です。
H(u1、u2)= T1 / T2
H(u2、u1)= T2 / T1
どこで
T1-ISO1で測定された期間
T2-ISO2で測定された期間
実験例
Hafele-Keating(以下のWikiリンクを参照)
クロノ速度を計算します。
地上に置かれた時計による飛行機の飛行(パート1)は101分続きました
飛行機の時計回りの飛行機の飛行(パート2)は100分続きました
H(p1、p2)= T1 / T2 = 101min / 100min
つまり ch1の時間で101分、ch2の時間で100分が経過
H(p2、p1)= T2 / T1 = 100min / 101min
つまり ch2の時間で100分、ch1の時間で101分が経過
そのため、MOVING飛行機のクロノスピードは地上のクロノスピードよりも低くなります。
もっと...
実験データに基づく
-時間膨張の影響はオブジェクトの速度のみに起因し、その加速には依存しません。 (ミューオンに表示、以下のwikiリンクを参照)
対称の例Pand5461を分析しましょう
次に:
-2つの惑星(相互に静止している)とISO1に関連する惑星があるとします。
-これらの惑星を過ぎて飛んでいるロケット1があります(ISO2を接続します)。 最初の最初の過去、次に2番目の過去。 さらに、ロケットは、ISO1の観点からは時間が移動しない(ISO2の時計で、惑星から惑星への飛行から1分経過した)ほどの非常に速い速度で飛行します。 しかし、惑星間の距離は非常に大きいです。 船はISO1で100年飛行します。
-ロケット1と同じロケット2を2番目の惑星に置きます
-イベント1:ロケットノーズ1とロケットノーズ2
-イベント2:ロケットテール1とロケットテール2の出会い
-event1とevent2の間の時間間隔が呼び出されます-「タッチ」
Pand5461が対称的な例で示したように、
( http://habrahabr.ru/post/151077/#comment_5870075 )、
ローレンツ変換を使用して計算する場合、クロノ速度は常に同じであることがわかります。
つまり 両方のロケットの持続時間「タッチ」:速い速度で移動するものと、惑星に静止するものの両方が同じになります。 つまり 両方のミサイルのダルタニャン-同じ回数座ってください!
しかし、私たちが知っているように:
これは物理的現実と矛盾します
-動くロケット1の時間はゆっくりと進むことができます(内部時計によれば、1分で巨大な距離をカバーしました-ダルタニャンは10回うずくまり、惑星では100年が経過しました-ダルタニャンは10,000回うずくまりました)。
-そして、惑星に静止しているロケット2を過ぎて飛行している間、両方のロケットの時間経過の速度(クロノ速度)が等しくなり、そこでのすべての物理的プロセスは同じ速度で実行され始めました???
PS
制御質問:
1)2つのイベント間の時間間隔を測定するために提案された方法が、私たちの物理的現実と矛盾しないことに同意しますか?
2)私が「期間」の概念に入れた物理的な意味を理解していますか? それが私たちの物理的現実と矛盾しないことに同意しますか?
3)あなたは私の証拠に同意します-1つのISOで測定される期間は、その測定方法に依存しません(1または2時間)
-同意しない場合でも、対称的な例では、時間間隔は同じ方法で比較されるため、結果に影響しません
4)同意しますか
Pand5461の対称の例とセニアの例との交差は、STRと物理的現実(実験データ)との矛盾の存在を示していますか?
トーク:
1.1。 同じISOの計算方法が異なると、速度も異なります。
セニア
」
はい。
物理量としての無益さをもう一度確認します。
」
-皮肉にも関わらず、誰もがこの点に同意しているようです:)
1.2。 クロノ速度の物理的意味を説明し(ダルタニャンによるクロノ速度の測定の例を使用)、実際には(SRTが説明しているように)ローレンツ変換を使用した計算で得られるのはSUCHではないかもしれないことを示すために。
セニア
」
やめて!
実際の実験なしではこれを証明できません。
」
( http://en.wikipedia.org/wiki/Special_relativity_theoryセクション:「相対論的時間拡張」)。 つまり 実際に行われた実験に。 そして、相対論的な科学者が到達した結論へ:
-飛行機で飛んでいる原子時計は、動かない原子時計に遅れをとっています。
-時間膨張の影響はオブジェクトの速度のみに起因し、その加速には依存しません。 (ミューオンに表示)
1.3。 クロノシフトに関する情報のないローレンツ変換は、クロノスピードの正しい計算ができないことを示すため。
セニア
」
1. SRTでの「クロノ速度」の正しい計算は原則として不可能です。SRTの観点からは、用語自体は正しくありません。
2.「正しい」結果とは何ですか?
」
-サービスステーションでの「クロノ速度」の正しい計算が不可能な場合は、用語の「不正確さ」だけが理由で、
「chrono-speed」の名前を「hz.chto」に変更できますが、それは私には何の違いもありません。この「hz.chto」を計算できる式が存在することが重要であり、それら自体は矛盾せず、それほど重要ではありません、この「hz.chto」の実験的測定方法があります。 「Hz.chto」-物理的な意味があります。
-サービスステーションで「クロノ速度」を正確に計算できない場合は、他の何らかの理由で、用語は間違っていませんが、サービスステーション
-正しい結果は、式で計算された結果がすべての場合に実験的に得られた結果に対応する場合です。
これらのすべての点について、私はすでにコメントで詳細を述べています。 各項目について、慎重に読んで理解し、意見を書いてください。
それらについて合意が得られたら、1.4を取り上げます。
合計:
p.1-すべてのサブパラグラフを議論した後にのみ、その意味がすべてに明確になると思います。
p.1.1。 誰もがこれに同意します。
p.1.2。 議論の中で...
p.1.3。 議論の中で...
さて、あなたは分析的に欲しい-ここで、お願いします、私はあなたにカードを明らかにします:)
最初の最も重要な点は、SRTのフレームワーク内で反論することは不可能であることです。 矛盾の存在を示すためには、問題について質的に異なる「レベル以上」の考察に到達する必要があります。 記事の冒頭でウォームアップタスクを引用したのは無駄ではありませんでした。その解決策のそれぞれは、標準フレームワーク内では解決できない問題に対する質的に新しいアプローチであるためです。 (実際、私は5つの解決策を見つけました。他の誰かが5eを見つけたかどうかを本当に知りたかったのですが、これらの解決策はさらにあります)。 しかし、私は脱線し、パラドックスに移ります。
まず、「時間」の概念を定義する必要があります。 アインシュタインの概念よりもこの概念のより一般的な定式化を行い、それによってSRTの抑圧を残します。
時間は、一定の均等に繰り返されるイベントの繰り返し回数です。
確かに、あなたは何でも何でも時間を測定できることを認めなければなりません。 たとえば、ボアの収縮体の長さはオウムによって測定でき、バス停での路面電車の待ち時間は、クリックした種子からのスキンの数によって測定できます。
これで、サービスステーションに従わない時計を作成できます。
たとえば、時計を閃光と見なす場合、実験の開始以降の閃光の回数(最初の閃光ではmT = 0)が時計の指標になります。
さらに、実験ではmT = 10回のフラッシュが続くと考えています。 鉄道線路に沿って、互いに等距離を置いて、タッチセンサー付きの電球を10個配置します(センサーと電球は同じポイントにあると考えています)。 各電球の下に、0、1、2 ... 9で始まる番号を書きます-これは、時間のスケール+ 1番目のオブザーバー(クローンダルタニャン)を置きます。
実験を開始します。
列車は鉄道線路に沿って均一かつ直線的に移動します。 その上には、電子メールを閉じるタッチセンサーがあります。 プラットフォームの電球センサーに触れると、電源が入ります。
電車の中にいるダルタニャンの仕事(電車のタッチセンサーと同じポイントに位置する)は、各閃光で1スクワットを実行します。観測者は、固定されたプラットフォームで閃いた光の隣に立っています。
もっと...
-列車は最初の電球まで引き上げられて点灯します。 mT = mT '= 0(最初のフラッシュ)
ダルタニャーナと電球の隣に立っているオブザーバーは、ISOについて同時にしゃがみ始めます(同じ地点にいるため)
-列車は2番目の電球まで引き上げられ、点灯します。 mT = mT '= 1(2回目のフラッシュ)
ご覧のとおり、チューブクロックは同期しています。
d'Artagnanはフラッシュをカウントし、それらに従って時間を決定しますmT '、オブザーバーはスケールの時間mTを決定します(数値は電球の隣にありますが、数値は例えば電球の色でコード化でき、d'Artagnanはスケールの時間も決定しますが、これは重要ではありません)
-...
-電車は10番目の電球まで引き上げられ、点灯します。 mT = mT '= 9(10回目のフラッシュ)
実験終了
見ての通り:
1. mT = mT '= 9ランプ時間までに列車およびプラットフォームで経過した時間
2.ランプの時間によると、電車のダルタニャンは10回しゃがみ、ライトの横にある彼のクローンも10回しゃがみました。 合計で、彼らは同じ仕事をしました。
3.しかし、アインシュタイン時計(ローレンツ変換)から判断すると、プラットホームt '<tに比べて、電車での経過時間は短くなっています。 同時に、電車のダルタニャンとプラットホームのダルタニャンは合計で同じように疲れていましたが、アインシュタインの時計によれば、何らかの理由で古くなったものです。
質問:
それでは、アインシュタインの「減速した」時間の物理的な意味は何ですか?
-相対論者:
ローレンツ変換は、古典物理学(CF)の公理のサブセットに基づいて取得できます。 この事実は、SRTの一貫性の証明をCFの一貫性の証明に減らします。
( http://synset.com/en/Lorenz Transformations )
-疑い:
はい、しかし同時に、5番目の公理はCFの5番目の公理から除外されました。「1つの参照フレームで2つのイベントが同時に発生した場合、他のイベントで同時に発生します。」残りの4つの公理が不完全であるため、変換にALPHA定数が現れました。一般的な場合、任意の値をとることができますが、私たちの宇宙では0以上です。ローレンツ変換自体は、この定数を決して定義しません(したがって、矛盾しません)。 理論の追加の5つの仮説から決定されます。
CFからはALPHA =無限、STOからはALPHA =光の速度になります。 つまり 5番目の仮定は、SRTに暗黙的に導入されます。「1つの参照フレームで2つのイベントが同時に発生する場合、それらは、これに関連する他の動きで同時に発生しません。」そして、古典物理学の5番目の仮定と矛盾します。
結論:ローレンツ変換自体はCFと矛盾せず、SRTの仮定と矛盾します:アルファ= CFの場合、アルファ=無限大。
そのため、SRTの一貫性はCFの一貫性に基づくことはできません。
-相対論者:
私たちの紛争で最も重要な議論は、SRTの結果が多くの実験で確認されているということです。 そして、この理論は科学界で広く認識されています。
— :
, .
( http://synset.com/ru/__ ), wiki :
« , «», , . XIX-, XX- . , .»
— :
, . . , « », . ( http://ufn.ru/ufn70/ufn70_10/Russian/r7010e.pdf )
:
«
, .
»
«
. , (
7), «»
« » « »,
« » * * * ).
»
: , .
— :
1 2, 3 3, 1 2. .
例:
«
U>0. ?
」
: . , . !
, , . , 1 2 ( 3 ). , , , (.. ) – .
: 3 . ( : « , » , 3 – , , ). , 3 – ().
— :
, , , 3 , .
— :
, .
— :
, , , «» , , — . , «» – , ( ).
— :
, '.
« », , « ».
— :
…
— :
– , , ?
— :
. , .
, , , .
, . = , = .
, – , .
, « » ( http://ufn.ru/ru/articles/2004/8/c/ )
, , . ( ) .
つまり , – . = .
結論:
– , (). – , ( ) . / .
, – , . (- ), «» , . «» «» / – .. , . , «» .
– (/), / . «» — .. , , , , (//. ) .
:
( ) , ( - ) , , , .
, ( / ) , , – . - () – , .
«», . , , ( ), , – .
, – ( ) . , . , ( ), , , « » , , – .
4.
, – , C ( ).
, , . , , «» ( ). «» , «» .
, – , . (.. , « '» – ).
, , ( 0:07), , , () . . , , , 1/30 , — .
( , ) « »… : « » « '». , , ( ), …
王がセージに来て、「世界はどうですか?」と簡単な質問をすると、彼は「世界ではすべてが相対的であり、光の速度のみが一定であり、観察者の観点からは常に同じです」と答えました。 王は微笑んで、彼らの間で議論が勃発しました...
K:-つまり、相対性理論の原理は、それらのオブザーバーのための慣性参照システム(ISO)のすべての物理プロセスが同じように記述されるということですか?
M:-はい、これまでのところ、このシステムが静止しているか、均一に動いているかどうかを判断するために、閉じた物理システムにいるセージは成功していません。
K:-なぜ観察者の視点から見た光の速度が常に同じなのですか?
M:-この仮定は、アインシュタインという特別な相対性理論(STR)で非常に賢い賢人によって提唱されました。 この理論は非常に権威があり、多くの実験の結果は予測した結果に近いものです。
K:-外側にタッチセンサーが設置されている均一に移動する列車が地面にあるスポットライトを通過し、同時に点灯すると、列車のヘッドライトからの光とスポットライトからの光が同時に列車の経路上の観測者に届きますか?
M:-まあ...誰も直接実験を行っていない(観測者は電車の邪魔をすることを拒否している)、彼らはほとんど円を描いて光を間接的に測定しますが、一般的に、ほとんどの賢明な男性はそうです、光の速度は光源の速度に依存しないと信じています。
K:-SRTはどのような物理現象を説明していますか?
M:-さて、例えば、時間の膨張。
observer1のISOが、それに対して静止している別のobserver2のISOに対して移動する場合、移動するobserver1の時間はより遅くなります。 彼が立ち止まると、彼の時計は休んでいる観察者の時計に遅れをとって2、彼自身は若く見える。
M:-サイズはまだ小さくなっています。
基準の「固定」フレームに対する移動体の直線寸法が減少します。
M:-「同時性の相対性」という効果もあります。
空間的に間隔を空けた2つのイベント(たとえば、閃光)が移動する参照フレームで同時に発生した場合、それらは「動きのない」システムに関して同時ではありません。 同時性の相対性により、空間全体のさまざまな慣性基準システムのクロックを同期することができなくなります。
K:-しかし、これはすでに面白いです! しかし、1つのISOにあるクロックを同期できますか?
M:はい、そのような時計を同期する方法はアインシュタイン自身によって提案されました...
「それでは」王は考えながら言った。 「アインシュタイン、私は愚かな男を見ていませんが、私たちも靱皮で縫われていません。 明日はサービスステーションをチェックします! 私はこの理論に矛盾があるという結論に達しました。「賢者はにやにやに笑いました:「何千人もの賢人がSRTについて槍を破り、誰もそれを論破することができませんでした!」 「しかし、彼らは王ではありませんでした!」王は同様にcなウインクで答えて、彼らは一緒に笑いました。
同じ夜に王室令が出されました:
「命令する。
明日の朝までに、2/3光に等しい速度で均一かつ直線的に真空内を移動できる列車を構築します。 電車の始めに、外側からタッチセンサーを取り付けます。タッチセンサーは、内側にある電球に接続されます。 センサーがトリガーされると、ライトが点灯します。 列車の最後にまったく同じセンサーと電球を置きます。 列車の中央と内側、外側に1muの光センサーを設置し、列車の始点と終点からの光線の到着を記録します。
トラックを(空間内で)ポイントXからポイントYに舗装します。トラックの中央に、列車の長さに等しい距離に2つのタッチセンサーを置きます。列車の対応する開始/終了センサーに触れると、接続されている固定ランプが点灯します。
朝、王様は仕事を受け入れました。
巨大なスタジアムの真ん中に立って、空を狙った宇宙ロケット。 すべてのセンサーと電球が取り付けられました。 銀色の金属で覆われたケースには、太陽の光の中、Made in USSR品質マークが誇らしげに輝いていました。 集まった観客、招待された有名人、見物人は赤い旗を振って、「悲観主義者よ、あなたの頭の上に!」と唱えました。 一般的に、すべてを開始する準備ができていました...
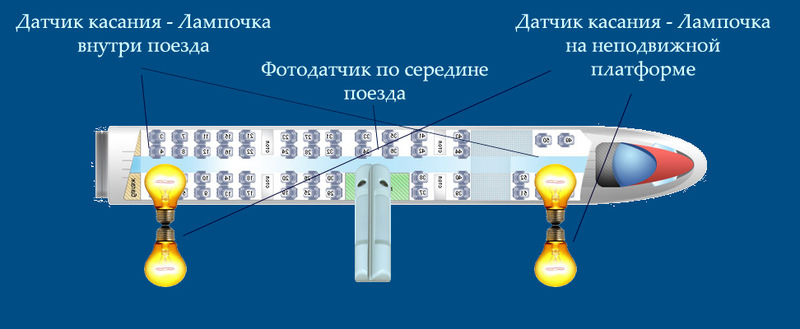
王は脇に立っている賢者たちに近づき、発表した。
K:-さて、同志、今、私たちは列車を起動し、サービスステーションに矛盾があることを確認します!
M:-これをどうやって納得させるのか?
K:-それはすべて泡についてです...
M:-どの泡に?
K:-緑の中で...しかし今はそれについてではありません。 実験の進捗状況について詳しく教えてください。
M:-?!
K:-それで。 列車は、敷設された線路に沿って均等に直線的に移動します。 固定タッチセンサーが設置されている場所を通過すると、タッチセンサーに触れ、タッチセンサーは電車の対応する場所でも機能するため、電車内にある照明とプラットフォームに固定されている照明は、電車で。
動いている列車の観測者の視点から、列車の始点と終点の電球からの光は、車の中央にあるセンサーに同時に届きます-同時に(彼の観点から、列車は停止しており、列車の始点から終点までの距離は同じです)
動いている列車に対して休んでいる観測者の観点から、列車の始点からの光は、列車の終点からの光よりも早く中央のセンサーに到達します。 これは、電車が動いているために発生し、電車の端からの光は、センサーが中央から離れるにつれて追いつく必要があります。 センサーに会うには、最初から来る光よりも長い距離を移動する必要があります。
K:-ご覧のとおり、顔には矛盾があります-動くISOトレインでは、センサーは光線の同時到着を記録します。 また、静止ISOでは、同じセンサーが光線の非同時到着を検出します!
M:(甘やかして笑う)-あなたは電車を始めることができません。なぜそれが起こるのかを説明します。 これは、「同時性の相対性」と呼ばれるSRTに続くよく知られた事実です。 つまり、アインシュタインの理論によれば、参照フレームの選択に応じて、離れた場所でのイベントの同時性は相対的なものになります。 つまり 各参照システムにはそれぞれ別のISOの時刻とは異なる独自の時刻があり、これらのISOのイベントは同時ではありません。
同時に、ローカルの同時性が保持されます。この例では、時刻x1でISOの列車のセンサーから発火した電球は、プラットフォームISOで同時に点灯しますが、x1とt1の時点で既に点灯しています。
K:(ニヤニヤ)-つまり、本質的に、独自の時間/空間とトリガーされた/トリガーされていないセンサーを持つ2つの宇宙があり、1つはISOトレインにあり、もう1つはISOプラットフォームにあるという事実に混乱していませんか?
M:-いいえ、SRTの枠組みでは、それは非常に自然なことです。すべてのイベントは、イベントが考慮できないISOに関係なく、1つのISOに関して決定されます。
K:-それで、私の議論はSRTの矛盾をあなたに納得させなかったのですか?
M:-いいえ
K:-じゃあ、待って...
M:-何を待つ必要がありますか?
王は、宴会テーブルから酸素カクテルを取り、肘掛け椅子に座り、ストローから数口を引いて、「見よ」と答えました。
約1時間が経過すると、観客はすでに退屈し始め、スタジアムでビールの下にビールの缶を投げ始めました。一部の人々はそこを歩いていた宇宙飛行士にさえ入ることができました...突然、スタジアムのゲートが開き、小さなトラックがロケットトレインまで行きました。 彼の体は明るい緑色に塗られており、その上にはっきりと見える半透明の緑色の泡があり、その真ん中に「緑色の泡-卸売りと小売り!」という碑文がありました。 車の外で、数人が緑色の箱を運んでロケット列車に引きずり込んで......
M:-これらのバブルは何ですか?
K:-これらは覆面捜査官であり、政府のために働いています...
M:-それにエージェントは何をするの?
K:-私は急進的な措置を取り、あなたに私の最後の議論を与えることにしました...王の最後の議論...あなたが反対することはできません...
M:(少し驚いた声で)-私たちの意見のために刑務所に送られますか?
K:-いや、いや、もちろん...あなた自身があなたの運命を選ぶ。
M:-どんな意味で?
K:-ISOによって生成された多くのユニバースとその時間と空間に関して、エラーを最小限に抑えることにしました。
K:-あなたが見たエージェントは電車に爆弾を積み込み、電車の中央にあるセンサーに接続しました。 センサーは、列車の始点と終点からの2つの光線の同時到着を修正する場合にのみ、爆弾をトリガーしてオンにするようにプログラムされています。
K:「今、電車を立ち上げます。今のところ、答えてみてください。目的地に到着するか、途中で爆発しますか?」
K:「私の忠実な助手、ダルタニャンはすでに電車の到着場所にいます。彼はすぐに戻ってきて、電車を見たら知らせます。
うーん、しかし、あなたの選択は大きくありません、2つのオプションだけがあります、そして、両方ともサービスステーションと矛盾します!
1. ISOプラットフォームに関しては、センサーへの光線の到着は同時ではなく、列車は爆発しません。
2.動いている列車のISOに関しては、センサーへの光線の到着は同時であり、列車は爆発します。
列車が爆発しない場合、プラットフォームISOは移動する列車のISOよりも利点(センサーに決定的な影響)を持ち、爆発する場合は反対になります。 つまり いずれにせよ、ISOの一部は等しくありません。これは、SRTの第1の前提に対する直接の矛盾です。SRTは、宇宙に割り当てられたISOはなく、すべてのISOが等しいと述べています。
K:-それで、電車は目的地に到着するのでしょうか... ダルタニャンはどのようなレポートで戻ってきますか?
まあ、それがすべてです。 この読書を楽しんで、王様の最後の質問に答えてくれたらと思います。 時計を見ると、世界の終わりがすでに来ていることがわかります... 2012年2月21日に記事を公開することは象徴的ですが、この世界の速度を制限します...しかし、その時点では通常のデザインがなく、ドラフトコピーでほこりっぽくなりました...
それでは、列車のロケットを発射して、実際に何が起こるかを見てみましょう。
私は王の従者ほど速くはありません。一晩でロケット列車を作成するのは現実的ではありません。数日かかりました... STOユニバースをモデル化し、方程式を使用して船の動きを説明するプログラムのソースコード(IDE C ++ Builder 2007) 。 今、私は、ピタゴラスの定理を証明した古代の数学者のように、たった1つの単語「Look!」で証明にコメントすることができます...しかし、21世紀では、3つの単語がより関連します:
プログラムでは「単純な動き」と呼ばれ、何かに反論するという目標を設定しません。 仕事は、STO宇宙の列車の単純で直線的な動きが、静止した観測者と列車にいる観測者の目を通してどのように見えるかを確認することです。 コンピューターモデルでは、オブジェクトの周囲の色付きの四角形は視覚的な視覚化のためだけのものであり、実際、オブジェクトはこれらの四角形の中央にある点に注意する必要があります。
主なものとして、固定のISO Kが選択され、これに関連して列車が移動します。 さらに、あるISOから別のISOに座標を変換することにより、列車に関連付けられたISO Kにあるポイントが計算されました。
オブジェクトの座標を取得するために使用された方程式は次のとおりです。
1.固定ISOのポイントの動き
x = x0 + v * t;
x-固定ISOのポイントの現在のx座標
x0-固定ISOのポイントの初期x座標
vは、固定ISOのポイントの速度です。
t-固定ISOのポイントの現在時刻
ここで、tはプログラムで指定されたステップによって異なり、指定されたtに対応するxを生成します。
2.動くISOで座標を取得する
ここに
相対論的速度加算として計算されたout_obj.v
out_obj.tは、実験の開始から経過した相対論的な時間間隔として計算されます
out_obj.xは、式x '= x0' + v '* t'によって計算されます。 移動するISOに対して既に計算された座標に従って
KからK 'への座標変換関数の完全なリスト:
, …
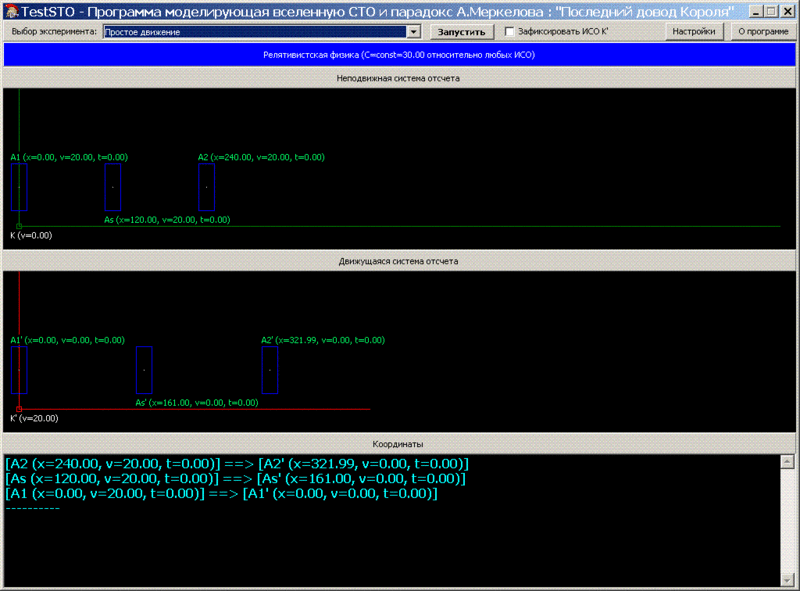
. Ex1_t0.
t=0 ( ):
:
— = 30
v – (. A1, As, A2) = 20 (2/3c)
x – , (.. — A2, 2(240), As(120), A1(0))
t — = 0 (.. 0)
:
— = 30
v’ – (. A1’, As’, A2’) = 0
x’ – 2’(321.99), As’(161), A1’(0)
t’ — = 0 (.. 0)
[A2 (x=240.00, v=20.00, t=0.00)] ==> [A2' (x=321.99, v=0.00, t=0.00)]
[As (x=120.00, v=20.00, t=0.00)] ==> [As' (x=161.00, v=0.00, t=0.00)]
[A1 (x=0.00, v=20.00, t=0.00)] ==> [A1' (x=0.00, v=0.00, t=0.00)]
.. : K’ (A2’ — A1’) = 321.99, K (A2 — A1) = 240. .. , K’ K.
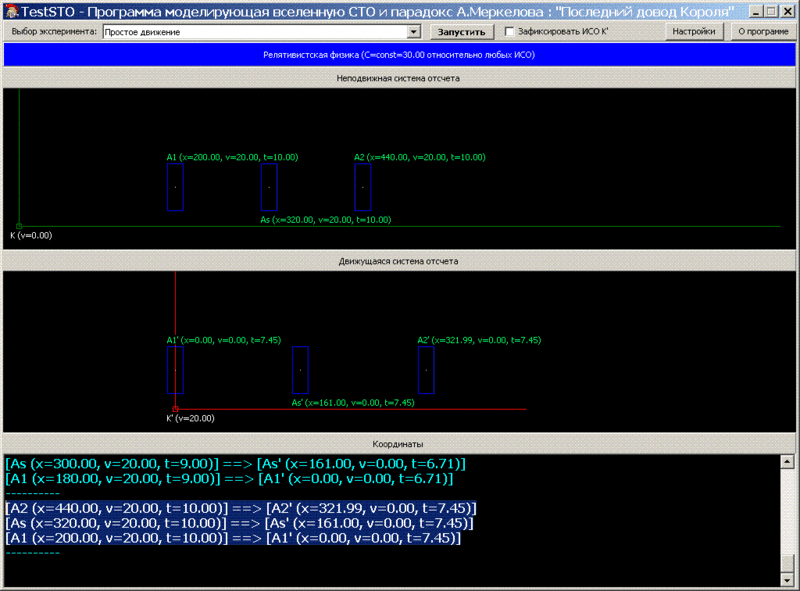
. Ex1_t10.
t — = 10 (.. 10)
[A2 (x=440.00, v=20.00, t=10.00)] ==> [A2' (x=321.99, v=0.00, t=7.45)]
[As (x=320.00, v=20.00, t=10.00)] ==> [As' (x=161.00, v=0.00, t=7.45)]
[A1 (x=200.00, v=20.00, t=10.00)] ==> [A1' (x=0.00, v=0.00, t=7.45)]
t (- ): K t=10, K’ t’=7.45. , K’ K, t’ 2,55 .
: « ( — )»
. 1 : F1 F2 ( ) – . D1 ( ) – , , .
, , , (A1,A2; A1’,A2’) (F1,F2; F1’,F2’).
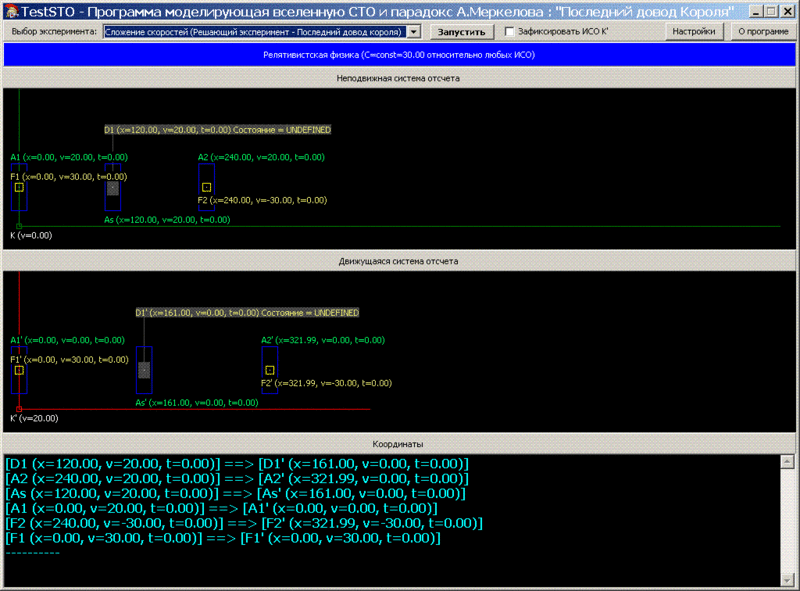
. Ex2_t0.
t=0: . A1-F1, A2-F2, A1’-F1’, A2’-F2’ , .. .
[D1 (x=120.00, v=20.00, t=0.00)] ==> [D1' (x=161.00, v=0.00, t=0.00)]
[A2 (x=240.00, v=20.00, t=0.00)] ==> [A2' (x=321.99, v=0.00, t=0.00)]
[As (x=120.00, v=20.00, t=0.00)] ==> [As' (x=161.00, v=0.00, t=0.00)]
[A1 (x=0.00, v=20.00, t=0.00)] ==> [A1' (x=0.00, v=0.00, t=0.00)]
[F2 (x=240.00, v=-30.00, t=0.00)] ==> [F2' (x=321.99, v=-30.00, t=0.00)]
[F1 (x=0.00, v=30.00, t=0.00)] ==> [F1' (x=0.00, v=30.00, t=0.00)]
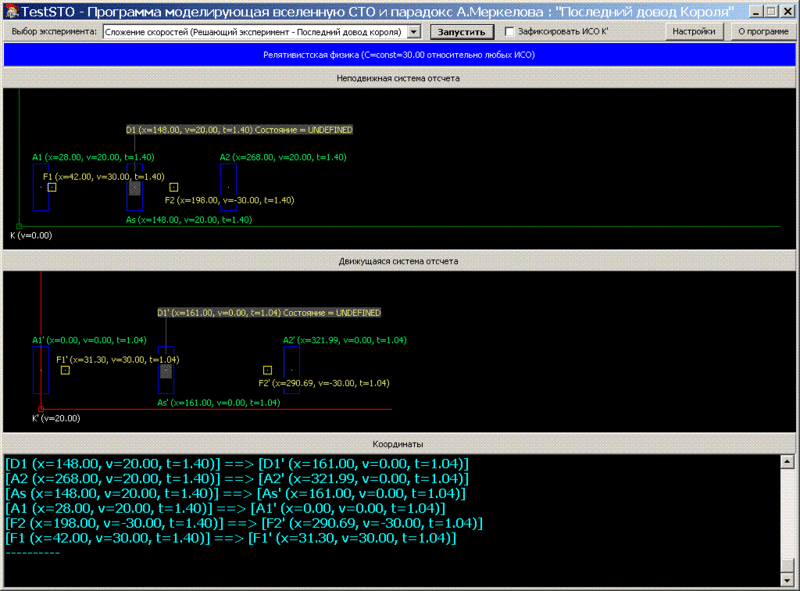
. Ex2_t1.40.
t=1.40: . , K F1-D1 > F2-D2, K’ F1’-D1’ = F2’-D2’
[D1 (x=148.00, v=20.00, t=1.40)] ==> [D1' (x=161.00, v=0.00, t=1.04)]
[A2 (x=268.00, v=20.00, t=1.40)] ==> [A2' (x=321.99, v=0.00, t=1.04)]
[As (x=148.00, v=20.00, t=1.40)] ==> [As' (x=161.00, v=0.00, t=1.04)]
[A1 (x=28.00, v=20.00, t=1.40)] ==> [A1' (x=0.00, v=0.00, t=1.04)]
[F2 (x=198.00, v=-30.00, t=1.40)] ==> [F2' (x=290.69, v=-30.00, t=1.04)]
[F1 (x=42.00, v=30.00, t=1.40)] ==> [F1' (x=31.30, v=30.00, t=1.04)]
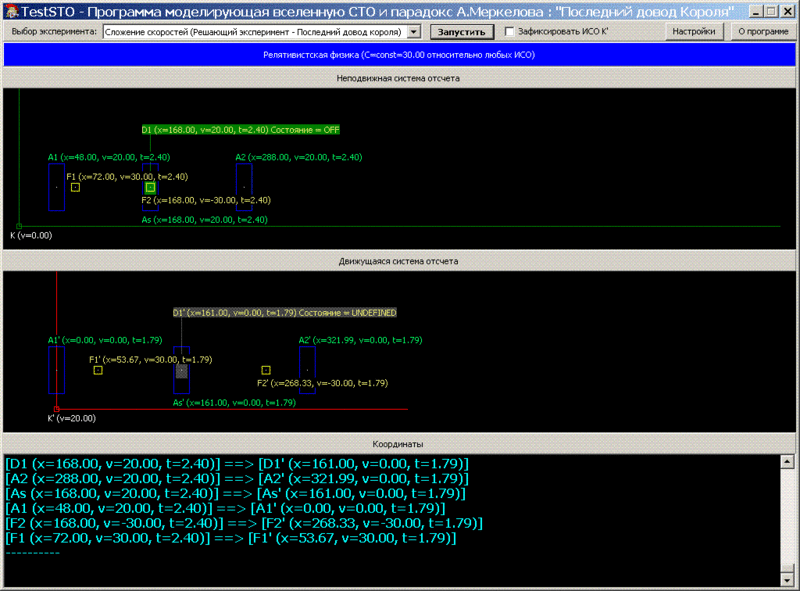
. Ex2_t2.40.
t2.40: , K, F2 D1 F2 – . , ! ’, , .
[D1 (x=168.00, v=20.00, t=2.40)] ==> [D1' (x=161.00, v=0.00, t=1.79)]
[A2 (x=288.00, v=20.00, t=2.40)] ==> [A2' (x=321.99, v=0.00, t=1.79)]
[As (x=168.00, v=20.00, t=2.40)] ==> [As' (x=161.00, v=0.00, t=1.79)]
[A1 (x=48.00, v=20.00, t=2.40)] ==> [A1' (x=0.00, v=0.00, t=1.79)]
[F2 (x=168.00, v=-30.00, t=2.40)] ==> [F2' (x=268.33, v=-30.00, t=1.79)]
[F1 (x=72.00, v=30.00, t=2.40)] ==> [F1' (x=53.67, v=30.00, t=1.79)]
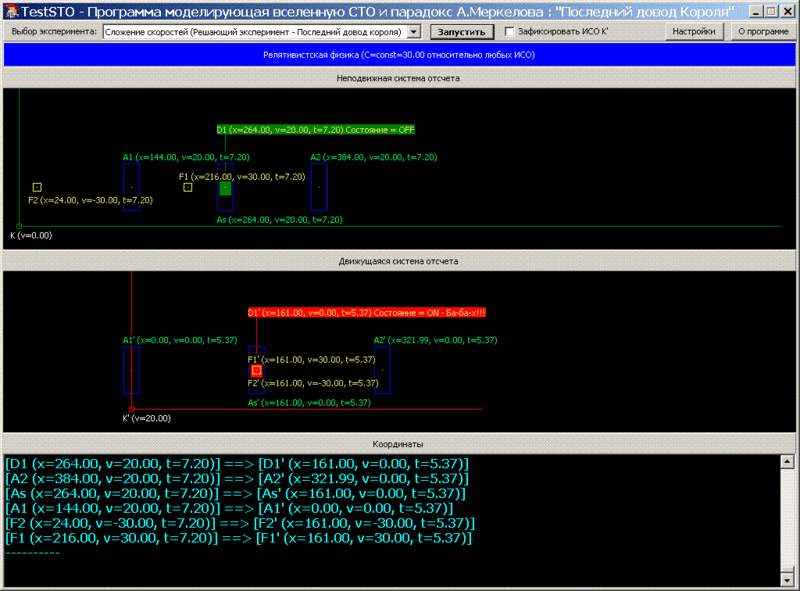
. Ex2_t7.20.
t=7.20: , K’, F2’ D1’ F2’ – . , , … . ’, , .
[D1 (x=264.00, v=20.00, t=7.20)] ==> [D1' (x=161.00, v=0.00, t=5.37)]
[A2 (x=384.00, v=20.00, t=7.20)] ==> [A2' (x=321.99, v=0.00, t=5.37)]
[As (x=264.00, v=20.00, t=7.20)] ==> [As' (x=161.00, v=0.00, t=5.37)]
[A1 (x=144.00, v=20.00, t=7.20)] ==> [A1' (x=0.00, v=0.00, t=5.37)]
[F2 (x=24.00, v=-30.00, t=7.20)] ==> [F2' (x=161.00, v=-30.00, t=5.37)]
[F1 (x=216.00, v=30.00, t=7.20)] ==> [F1' (x=161.00, v=30.00, t=5.37)]
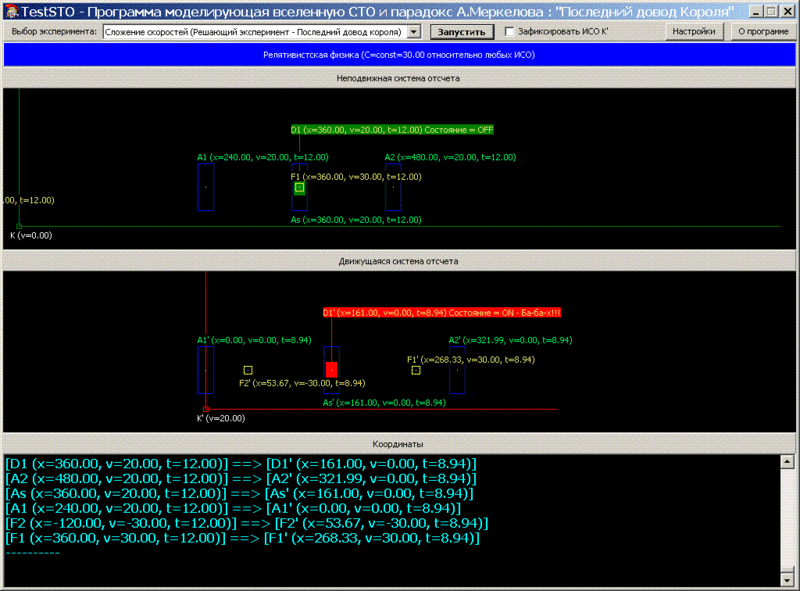
. Ex2_t12.
t=12.00: , , K, ( K’ ) F1 - D1.
[D1 (x=360.00, v=20.00, t=12.00)] ==> [D1' (x=161.00, v=0.00, t=8.94)]
[A2 (x=480.00, v=20.00, t=12.00)] ==> [A2' (x=321.99, v=0.00, t=8.94)]
[As (x=360.00, v=20.00, t=12.00)] ==> [As' (x=161.00, v=0.00, t=8.94)]
[A1 (x=240.00, v=20.00, t=12.00)] ==> [A1' (x=0.00, v=0.00, t=8.94)]
[F2 (x=-120.00, v=-30.00, t=12.00)] ==> [F2' (x=53.67, v=-30.00, t=8.94)]
[F1 (x=360.00, v=30.00, t=12.00)] ==> [F1' (x=268.33, v=30.00, t=8.94)]
:
’, ?
, , :
№1. ( ):
— . , , , , . , , () (/).
№2. – ( ):
— . , .
№3. . ( ):
— .
’ ( )?
A B, ’, (), A B, !
, ( ) ( ). . -, , .
, « ’ ( ) », A’ B’ / ( ).
A’ B’ ( ) , (.. – , , ) ( ) ( ). , , ( ), , . , M’, , « » .
, : «, , , ( ).» — !
, , ( ) / , , , .
:
, , , ( , ).
« », , . , , , « » , .
2 : « » — . 1 : « » , 1 () 2 (/ ) , – .
…
’ , - , . , . , , ’ -, - .
PS:
, , , . , , «» , , . , , , . , .
. 1.
(++Builder 2007) , exe Windows .
.
, – , .
,
(free_mind2@list.ru)
2014年6月7日の更新
ホスポダ、この投稿に対する最後のコメントから1年以上が経過したことをお知らせします。これについてもあなたは満足していると思います:)
議論の各当事者は納得がいかないままでしたが、それでも...同意しますが、議論するのは面白かったです;)
しかし...時間が経ち、もちろん私たち全員は真面目で忙しい人です...したがって、貴重な数秒を無駄にしないように、最近思いついた2分間の実験を見ることをお勧めします。
そして、表示後、相対性理論を擁護する議論があれば、少し議論することができます。
x ------- x
この記事の内容を理解するためには、ステレオタイプのない明確な頭を持つ必要があります。 したがって、まずは、同僚を楽しませるために5年ほど前に思いついた1つの簡単な問題を解決して、神経系を活性化することをお勧めします。
ウォームアップのタスク:
球の中には、そこから引き出す必要のある特定のオブジェクトがあります。 問題は抽象的であるため、物理法則に拘束されず、任意の方法を使用して解決できます。1つの条件があります-このオブジェクトは球を通過できず、球を破壊できません。
簡略化:
ゴム製のボールの内側には小石があり、引き抜く必要がありますが、ボールをナイフで刺したり、チェーンソーで挽いたりすることはできません。
私はこの問題を解決するための4つのオプションを考え出しました(たぶんもっと見つけるでしょう):
オプション1:
球の代わりに輪ゴムがテーブルの上にあり、ボタンが中央にあると想像してください。 テーブル上のボタンを移動すると、弾性バンドからボタンを引き出すことはできませんが、テーブルの上でボタンを持ち上げると、弾性バンドの上に簡単に移動して外側に置くことができます。 球体の場合も同様です。3番目の代わりに、オブジェクトを4番目の次元に転送します。
オプション2:
タスクは、指定されたオブジェクトは球を通過できないと言っていますが、他のタイプのオブジェクトも通過できないとは言われていないため、このオブジェクトを球を通過できる別のタイプのオブジェクトに変換してから、元に戻すことができますソース。 たとえば、小石を蒸発させてゴムを通過させることができるガスを生成し、出てきたガスから再び物体を形成することができます。
オプション3:
電磁波の助けを借りてオブジェクト(または球体を通過できる他の信号)は、その構造に関する情報を球体の外部に転送します。 そこで、これらのデータに基づいて、オブジェクトのコピーが作成され、その後、球内のオブジェクトが自己破壊します。
オプション4:
球を無限に拡張するか、同じことを行い、オブジェクトが存在する宇宙を縮小して球内に収まると同時に、この宇宙からのオブジェクトが境界に近づいて検出しようとする場合、球を常に拡張させることができますスコープ。 そうすれば、私たちのオブジェクトは宇宙を自由に動き回ることができ、球体に限定されることはありません。さらに、球体は、その存在を証明することができないため、この宇宙のあらゆるオブジェクトに関して存在しなくなります。 言い換えると、球体を破壊することなく、球体を消滅させました。つまり、オブジェクトの宇宙を裏返しました。
畳み込みを動かして喜んでいただけたことを願っています。今、私たちは最も興味深いものに目を向けています。
パラドックス:「時間間隔」
証明のキーポイント:
1. SRTで使用されるローレンツ変換には、クロノスピードを正しく計算するための基準はありません。
1.1。 同じISOの計算方法が異なると、速度も異なります。
1.2。 クロノ速度の物理的意味を説明し(ダルタニャンによるクロノ速度の測定の例を使用)、実際には(SRTが説明しているように)ローレンツ変換を使用した計算で得られるのはSUCHではないかもしれないことを示すために。
1.3。 クロノシフトに関する情報のないローレンツ変換は、クロノスピードの正しい計算ができないことを示すため。
証明:
私の理由は次のとおりです。
この段落の目的は、クロノスピードの論理的/物理的意味を示すことです。
最大の仕事は、「クロノスピード」という言葉の私の論理的な説明の後、あなた自身がそれを測定する方法の結論に達することです。
最小のタスクは、例として時間間隔の測定/計算を行う方法が正しいことに同意することです。
それでは始めましょう。
クロノスピードの意味を理解するには、2つのイベント間の時間(時間間隔)を測定する方法に同意する必要があります。
次の2つのオプションがあります。
1)両方のイベントは空間の1つのポイントで発生します
2)イベントは空間のさまざまなポイントで発生します
時間間隔では、通常の時間だけでなく、2つのイベントの間に行うダルタニャンスクワットの数を測定します。 一見、これは余分な重複のように思われるかもしれませんが、後で示すように、ダルタニャンの導入は基本的に理解するためのものです。 あなたの目を開くのはそれです。
1)タイムラプス測定手順
両方のイベントが空間の1つのポイントで発生する場合
-イベントが行われる時点で数時間あります
-時計はダルタニャンです
-event1の時点で、クロックt = 0、d'Artagnanがしゃがみ始め、しゃがんだ数k = 0
-クロックt = Tのevent2の時点で、ダルタニャンはしゃがむのをやめk = K
-結果:測定された期間は、時間ごとにT、ダルタニャンごとにKです。
2)タイムラプス測定手順
空間のさまざまなポイントでイベントが発生する場合
-d'Artagnansを使用したCh1とCh2のクロックは、event1とevent2のポイントに配置されます(クロックは互いに相対的に静止しています)
-クロックCh1とCh2はアインシュタイン法によって同期され、その後永久に同期します(ISO Ch1 / Ch2で)
-11 t = 0のpoint1のevent1の瞬間、d'Artagnanはスクワットを開始しますk = 0
-22 t = Tのpoint2のevent2の時点
-Ch2は、このデータ(t = T)を含むSMSを、まだしゃがんでいるCh1のd'Artagnanに送信します。 (SMSは重要ではありません。信号または伝書鳩の場合があります。測定に影響しないため、重要ではありません)
-Chs1でsmsku d'Artagnanを受け取った人は、しゃがむのをやめ、彼の日記を調べます。 ダルタニャンがしゃがむと、彼らはスクワット雑誌を保管していることがわかります:)。 この雑誌には、「時間」と「すでに完了したスクワットの数」という2つのコラムしかありませんが、時間Tで、Ch1のd'ArtagnanがKスクワットを完了したことがわかりました。
-結果:測定された期間は、時間ごとにT、ダルタニャンごとにKです。
もっと...
これで、1つのポイントでの2つのイベント(1)と異なるポイントでの2つのイベント(2)の時間間隔を測定できます。
測定された期間の物理的な意味は、 d'Artagnanがevent1とevent2の間に実行することができたスクワットの数と見なします。
これは重要ではありません-どのようにして、1mまたは2mの期間を測定しても、これからのスクワット数は変わりません。
1つのISOで測定される時間間隔は、その測定方法に依存しないことを証明しましょう((1)または(2)):
P1 / P2-同期して、つまり 同じ読み値t = Tを同時に表示します。 もちろん、ISO Ch1 / Ch2に関しては。
Ch2でTを思い出すと、Ch1で同時にそれを断言できます。 同じ瞬間t = T つまり 同期クロックの読み取り値は、それらの間の距離に依存しません(1つのISOで)。 つまり 実際、ISO Ch1 / Ch2で時間間隔を測定したのは1時間Ch1だけでした。 測定の完了の瞬間は、Ch2の同期稼働時間によって行われました。Ch2の読み取り値は、Ch1の読み取り値とまったく同じです(ISO Ch1 / Ch2で)。
「イベントの期間」の概念を定義します。
イベントABの期間は、1つのISOで測定されたイベントAとイベントBの間の期間です。
これで、クロノスピードの概念を紹介できます。
CHRONIC SPEED(H)は、ISOごとにONEおよびSAMEイベントのDURATIONが何回異なるかを示す係数です。
ISO2に対するISO1速度は、ISO1のevent1とevent2の間で測定された時間間隔と、ISO 2のTEM SAME event1とevent2の間で測定された時間間隔の比率です。
クロノ速度の実験的測定の場合 -ISO1ではh1(T1)時間、ISO2ではh2(T2)時間のONEおよびSAMEイベントの継続時間を測定するだけで十分です。
H(u1、u2)= T1 / T2
H(u2、u1)= T2 / T1
どこで
T1-ISO1で測定された期間
T2-ISO2で測定された期間
実験例
Hafele-Keating(以下のWikiリンクを参照)
クロノ速度を計算します。
地上に置かれた時計による飛行機の飛行(パート1)は101分続きました
飛行機の時計回りの飛行機の飛行(パート2)は100分続きました
H(p1、p2)= T1 / T2 = 101min / 100min
つまり ch1の時間で101分、ch2の時間で100分が経過
H(p2、p1)= T2 / T1 = 100min / 101min
つまり ch2の時間で100分、ch1の時間で101分が経過
そのため、MOVING飛行機のクロノスピードは地上のクロノスピードよりも低くなります。
もっと...
実験データに基づく
-時間膨張の影響はオブジェクトの速度のみに起因し、その加速には依存しません。 (ミューオンに表示、以下のwikiリンクを参照)
対称の例Pand5461を分析しましょう
セニアの例とそれを交差させる
次に:
-2つの惑星(相互に静止している)とISO1に関連する惑星があるとします。
-これらの惑星を過ぎて飛んでいるロケット1があります(ISO2を接続します)。 最初の最初の過去、次に2番目の過去。 さらに、ロケットは、ISO1の観点からは時間が移動しない(ISO2の時計で、惑星から惑星への飛行から1分経過した)ほどの非常に速い速度で飛行します。 しかし、惑星間の距離は非常に大きいです。 船はISO1で100年飛行します。
-ロケット1と同じロケット2を2番目の惑星に置きます
-イベント1:ロケットノーズ1とロケットノーズ2
-イベント2:ロケットテール1とロケットテール2の出会い
-event1とevent2の間の時間間隔が呼び出されます-「タッチ」
Pand5461が対称的な例で示したように、
( http://habrahabr.ru/post/151077/#comment_5870075 )、
ローレンツ変換を使用して計算する場合、クロノ速度は常に同じであることがわかります。
つまり 両方のロケットの持続時間「タッチ」:速い速度で移動するものと、惑星に静止するものの両方が同じになります。 つまり 両方のミサイルのダルタニャン-同じ回数座ってください!
しかし、私たちが知っているように:
これは物理的現実と矛盾します
-動くロケット1の時間はゆっくりと進むことができます(内部時計によれば、1分で巨大な距離をカバーしました-ダルタニャンは10回うずくまり、惑星では100年が経過しました-ダルタニャンは10,000回うずくまりました)。
-そして、惑星に静止しているロケット2を過ぎて飛行している間、両方のロケットの時間経過の速度(クロノ速度)が等しくなり、そこでのすべての物理的プロセスは同じ速度で実行され始めました???
PS
制御質問:
1)2つのイベント間の時間間隔を測定するために提案された方法が、私たちの物理的現実と矛盾しないことに同意しますか?
2)私が「期間」の概念に入れた物理的な意味を理解していますか? それが私たちの物理的現実と矛盾しないことに同意しますか?
3)あなたは私の証拠に同意します-1つのISOで測定される期間は、その測定方法に依存しません(1または2時間)
-同意しない場合でも、対称的な例では、時間間隔は同じ方法で比較されるため、結果に影響しません
4)同意しますか
Pand5461の対称の例とセニアの例との交差は、STRと物理的現実(実験データ)との矛盾の存在を示していますか?
トーク:
1.1。 同じISOの計算方法が異なると、速度も異なります。
セニア
」
はい。
物理量としての無益さをもう一度確認します。
」
-皮肉にも関わらず、誰もがこの点に同意しているようです:)
1.2。 クロノ速度の物理的意味を説明し(ダルタニャンによるクロノ速度の測定の例を使用)、実際には(SRTが説明しているように)ローレンツ変換を使用した計算で得られるのはSUCHではないかもしれないことを示すために。
セニア
」
やめて!
実際の実験なしではこれを証明できません。
」
-私は次の実験に依存しています:
( http://en.wikipedia.org/wiki/Special_relativity_theoryセクション:「相対論的時間拡張」)。 つまり 実際に行われた実験に。 そして、相対論的な科学者が到達した結論へ:
-飛行機で飛んでいる原子時計は、動かない原子時計に遅れをとっています。
-時間膨張の影響はオブジェクトの速度のみに起因し、その加速には依存しません。 (ミューオンに表示)
1.3。 クロノシフトに関する情報のないローレンツ変換は、クロノスピードの正しい計算ができないことを示すため。
セニア
」
1. SRTでの「クロノ速度」の正しい計算は原則として不可能です。SRTの観点からは、用語自体は正しくありません。
2.「正しい」結果とは何ですか?
」
-サービスステーションでの「クロノ速度」の正しい計算が不可能な場合は、用語の「不正確さ」だけが理由で、
「chrono-speed」の名前を「hz.chto」に変更できますが、それは私には何の違いもありません。この「hz.chto」を計算できる式が存在することが重要であり、それら自体は矛盾せず、それほど重要ではありません、この「hz.chto」の実験的測定方法があります。 「Hz.chto」-物理的な意味があります。
-サービスステーションで「クロノ速度」を正確に計算できない場合は、他の何らかの理由で、用語は間違っていませんが、サービスステーション
-正しい結果は、式で計算された結果がすべての場合に実験的に得られた結果に対応する場合です。
これらのすべての点について、私はすでにコメントで詳細を述べています。 各項目について、慎重に読んで理解し、意見を書いてください。
それらについて合意が得られたら、1.4を取り上げます。
合計:
p.1-すべてのサブパラグラフを議論した後にのみ、その意味がすべてに明確になると思います。
p.1.1。 誰もがこれに同意します。
p.1.2。 議論の中で...
p.1.3。 議論の中で...
パラドックス:「ダルタニャンの時間」
さて、あなたは分析的に欲しい-ここで、お願いします、私はあなたにカードを明らかにします:)
最初の最も重要な点は、SRTのフレームワーク内で反論することは不可能であることです。 矛盾の存在を示すためには、問題について質的に異なる「レベル以上」の考察に到達する必要があります。 記事の冒頭でウォームアップタスクを引用したのは無駄ではありませんでした。その解決策のそれぞれは、標準フレームワーク内では解決できない問題に対する質的に新しいアプローチであるためです。 (実際、私は5つの解決策を見つけました。他の誰かが5eを見つけたかどうかを本当に知りたかったのですが、これらの解決策はさらにあります)。 しかし、私は脱線し、パラドックスに移ります。
まず、「時間」の概念を定義する必要があります。 アインシュタインの概念よりもこの概念のより一般的な定式化を行い、それによってSRTの抑圧を残します。
時間は、一定の均等に繰り返されるイベントの繰り返し回数です。
確かに、あなたは何でも何でも時間を測定できることを認めなければなりません。 たとえば、ボアの収縮体の長さはオウムによって測定でき、バス停での路面電車の待ち時間は、クリックした種子からのスキンの数によって測定できます。
これで、サービスステーションに従わない時計を作成できます。
たとえば、時計を閃光と見なす場合、実験の開始以降の閃光の回数(最初の閃光ではmT = 0)が時計の指標になります。
さらに、実験ではmT = 10回のフラッシュが続くと考えています。 鉄道線路に沿って、互いに等距離を置いて、タッチセンサー付きの電球を10個配置します(センサーと電球は同じポイントにあると考えています)。 各電球の下に、0、1、2 ... 9で始まる番号を書きます-これは、時間のスケール+ 1番目のオブザーバー(クローンダルタニャン)を置きます。
実験を開始します。
列車は鉄道線路に沿って均一かつ直線的に移動します。 その上には、電子メールを閉じるタッチセンサーがあります。 プラットフォームの電球センサーに触れると、電源が入ります。
電車の中にいるダルタニャンの仕事(電車のタッチセンサーと同じポイントに位置する)は、各閃光で1スクワットを実行します。観測者は、固定されたプラットフォームで閃いた光の隣に立っています。
もっと...
-列車は最初の電球まで引き上げられて点灯します。 mT = mT '= 0(最初のフラッシュ)
ダルタニャーナと電球の隣に立っているオブザーバーは、ISOについて同時にしゃがみ始めます(同じ地点にいるため)

-列車は2番目の電球まで引き上げられ、点灯します。 mT = mT '= 1(2回目のフラッシュ)
ご覧のとおり、チューブクロックは同期しています。
d'Artagnanはフラッシュをカウントし、それらに従って時間を決定しますmT '、オブザーバーはスケールの時間mTを決定します(数値は電球の隣にありますが、数値は例えば電球の色でコード化でき、d'Artagnanはスケールの時間も決定しますが、これは重要ではありません)
-...
-電車は10番目の電球まで引き上げられ、点灯します。 mT = mT '= 9(10回目のフラッシュ)
実験終了

見ての通り:
1. mT = mT '= 9ランプ時間までに列車およびプラットフォームで経過した時間
2.ランプの時間によると、電車のダルタニャンは10回しゃがみ、ライトの横にある彼のクローンも10回しゃがみました。 合計で、彼らは同じ仕事をしました。
3.しかし、アインシュタイン時計(ローレンツ変換)から判断すると、プラットホームt '<tに比べて、電車での経過時間は短くなっています。 同時に、電車のダルタニャンとプラットホームのダルタニャンは合計で同じように疲れていましたが、アインシュタインの時計によれば、何らかの理由で古くなったものです。
質問:
それでは、アインシュタインの「減速した」時間の物理的な意味は何ですか?
長所と短所(2つの視点間の論争):
理由1。
-相対論者:
ローレンツ変換は、古典物理学(CF)の公理のサブセットに基づいて取得できます。 この事実は、SRTの一貫性の証明をCFの一貫性の証明に減らします。
( http://synset.com/en/Lorenz Transformations )
-疑い:
はい、しかし同時に、5番目の公理はCFの5番目の公理から除外されました。「1つの参照フレームで2つのイベントが同時に発生した場合、他のイベントで同時に発生します。」残りの4つの公理が不完全であるため、変換にALPHA定数が現れました。一般的な場合、任意の値をとることができますが、私たちの宇宙では0以上です。ローレンツ変換自体は、この定数を決して定義しません(したがって、矛盾しません)。 理論の追加の5つの仮説から決定されます。
CFからはALPHA =無限、STOからはALPHA =光の速度になります。 つまり 5番目の仮定は、SRTに暗黙的に導入されます。「1つの参照フレームで2つのイベントが同時に発生する場合、それらは、これに関連する他の動きで同時に発生しません。」そして、古典物理学の5番目の仮定と矛盾します。
結論:ローレンツ変換自体はCFと矛盾せず、SRTの仮定と矛盾します:アルファ= CFの場合、アルファ=無限大。
そのため、SRTの一貫性はCFの一貫性に基づくことはできません。
引数2。
-相対論者:
私たちの紛争で最も重要な議論は、SRTの結果が多くの実験で確認されているということです。 そして、この理論は科学界で広く認識されています。
— :
, .
( http://synset.com/ru/__ ), wiki :
« , «», , . XIX-, XX- . , .»
— :
, . . , « », . ( http://ufn.ru/ufn70/ufn70_10/Russian/r7010e.pdf )
:
«
, .
»
«
. , (
7), «»
« » « »,
« » * * * ).
»
: , .
3.
— :
1 2, 3 3, 1 2. .
例:
«
U>0. ?
」
: . , . !
, , . , 1 2 ( 3 ). , , , (.. ) – .
: 3 . ( : « , » , 3 – , , ). , 3 – ().
— :
, , , 3 , .
— :
, .
— :
, , , «» , , — . , «» – , ( ).
4.
— :
, '.
« », , « ».
— :
…
5.
— :
– , , ?
— :
. , .
, , , .
, . = , = .
, – , .
, « » ( http://ufn.ru/ru/articles/2004/8/c/ )
, , . ( ) .
つまり , – . = .
結論:
– , (). – , ( ) . / .
, – , . (- ), «» , . «» «» / – .. , . , «» .
– (/), / . «» — .. , , , , (//. ) .
:
( ) , ( - ) , , , .
, ( / ) , , – . - () – , .
«», . , , ( ), , – .
, – ( ) . , . , ( ), , , « » , , – .
4.
, – , C ( ).
, , . , , «» ( ). «» , «» .
, – , . (.. , « '» – ).
, , ( 0:07), , , () . . , , , 1/30 , — .
( , ) « »… : « » « '». , , ( ), …
, :
王がセージに来て、「世界はどうですか?」と簡単な質問をすると、彼は「世界ではすべてが相対的であり、光の速度のみが一定であり、観察者の観点からは常に同じです」と答えました。 王は微笑んで、彼らの間で議論が勃発しました...
K:-つまり、相対性理論の原理は、それらのオブザーバーのための慣性参照システム(ISO)のすべての物理プロセスが同じように記述されるということですか?
M:-はい、これまでのところ、このシステムが静止しているか、均一に動いているかどうかを判断するために、閉じた物理システムにいるセージは成功していません。
K:-なぜ観察者の視点から見た光の速度が常に同じなのですか?
M:-この仮定は、アインシュタインという特別な相対性理論(STR)で非常に賢い賢人によって提唱されました。 この理論は非常に権威があり、多くの実験の結果は予測した結果に近いものです。
K:-外側にタッチセンサーが設置されている均一に移動する列車が地面にあるスポットライトを通過し、同時に点灯すると、列車のヘッドライトからの光とスポットライトからの光が同時に列車の経路上の観測者に届きますか?
M:-まあ...誰も直接実験を行っていない(観測者は電車の邪魔をすることを拒否している)、彼らはほとんど円を描いて光を間接的に測定しますが、一般的に、ほとんどの賢明な男性はそうです、光の速度は光源の速度に依存しないと信じています。
K:-SRTはどのような物理現象を説明していますか?
M:-さて、例えば、時間の膨張。
observer1のISOが、それに対して静止している別のobserver2のISOに対して移動する場合、移動するobserver1の時間はより遅くなります。 彼が立ち止まると、彼の時計は休んでいる観察者の時計に遅れをとって2、彼自身は若く見える。
M:-サイズはまだ小さくなっています。
基準の「固定」フレームに対する移動体の直線寸法が減少します。
M:-「同時性の相対性」という効果もあります。
空間的に間隔を空けた2つのイベント(たとえば、閃光)が移動する参照フレームで同時に発生した場合、それらは「動きのない」システムに関して同時ではありません。 同時性の相対性により、空間全体のさまざまな慣性基準システムのクロックを同期することができなくなります。
K:-しかし、これはすでに面白いです! しかし、1つのISOにあるクロックを同期できますか?
M:はい、そのような時計を同期する方法はアインシュタイン自身によって提案されました...
「それでは」王は考えながら言った。 「アインシュタイン、私は愚かな男を見ていませんが、私たちも靱皮で縫われていません。 明日はサービスステーションをチェックします! 私はこの理論に矛盾があるという結論に達しました。「賢者はにやにやに笑いました:「何千人もの賢人がSRTについて槍を破り、誰もそれを論破することができませんでした!」 「しかし、彼らは王ではありませんでした!」王は同様にcなウインクで答えて、彼らは一緒に笑いました。
同じ夜に王室令が出されました:
「命令する。
明日の朝までに、2/3光に等しい速度で均一かつ直線的に真空内を移動できる列車を構築します。 電車の始めに、外側からタッチセンサーを取り付けます。タッチセンサーは、内側にある電球に接続されます。 センサーがトリガーされると、ライトが点灯します。 列車の最後にまったく同じセンサーと電球を置きます。 列車の中央と内側、外側に1muの光センサーを設置し、列車の始点と終点からの光線の到着を記録します。
トラックを(空間内で)ポイントXからポイントYに舗装します。トラックの中央に、列車の長さに等しい距離に2つのタッチセンサーを置きます。列車の対応する開始/終了センサーに触れると、接続されている固定ランプが点灯します。
朝、王様は仕事を受け入れました。
巨大なスタジアムの真ん中に立って、空を狙った宇宙ロケット。 すべてのセンサーと電球が取り付けられました。 銀色の金属で覆われたケースには、太陽の光の中、Made in USSR品質マークが誇らしげに輝いていました。 集まった観客、招待された有名人、見物人は赤い旗を振って、「悲観主義者よ、あなたの頭の上に!」と唱えました。 一般的に、すべてを開始する準備ができていました...

王は脇に立っている賢者たちに近づき、発表した。
K:-さて、同志、今、私たちは列車を起動し、サービスステーションに矛盾があることを確認します!
M:-これをどうやって納得させるのか?
K:-それはすべて泡についてです...
M:-どの泡に?
K:-緑の中で...しかし今はそれについてではありません。 実験の進捗状況について詳しく教えてください。
M:-?!
K:-それで。 列車は、敷設された線路に沿って均等に直線的に移動します。 固定タッチセンサーが設置されている場所を通過すると、タッチセンサーに触れ、タッチセンサーは電車の対応する場所でも機能するため、電車内にある照明とプラットフォームに固定されている照明は、電車で。
動いている列車の観測者の視点から、列車の始点と終点の電球からの光は、車の中央にあるセンサーに同時に届きます-同時に(彼の観点から、列車は停止しており、列車の始点から終点までの距離は同じです)
動いている列車に対して休んでいる観測者の観点から、列車の始点からの光は、列車の終点からの光よりも早く中央のセンサーに到達します。 これは、電車が動いているために発生し、電車の端からの光は、センサーが中央から離れるにつれて追いつく必要があります。 センサーに会うには、最初から来る光よりも長い距離を移動する必要があります。
K:-ご覧のとおり、顔には矛盾があります-動くISOトレインでは、センサーは光線の同時到着を記録します。 また、静止ISOでは、同じセンサーが光線の非同時到着を検出します!
M:(甘やかして笑う)-あなたは電車を始めることができません。なぜそれが起こるのかを説明します。 これは、「同時性の相対性」と呼ばれるSRTに続くよく知られた事実です。 つまり、アインシュタインの理論によれば、参照フレームの選択に応じて、離れた場所でのイベントの同時性は相対的なものになります。 つまり 各参照システムにはそれぞれ別のISOの時刻とは異なる独自の時刻があり、これらのISOのイベントは同時ではありません。
同時に、ローカルの同時性が保持されます。この例では、時刻x1でISOの列車のセンサーから発火した電球は、プラットフォームISOで同時に点灯しますが、x1とt1の時点で既に点灯しています。
K:(ニヤニヤ)-つまり、本質的に、独自の時間/空間とトリガーされた/トリガーされていないセンサーを持つ2つの宇宙があり、1つはISOトレインにあり、もう1つはISOプラットフォームにあるという事実に混乱していませんか?
M:-いいえ、SRTの枠組みでは、それは非常に自然なことです。すべてのイベントは、イベントが考慮できないISOに関係なく、1つのISOに関して決定されます。
K:-それで、私の議論はSRTの矛盾をあなたに納得させなかったのですか?
M:-いいえ
K:-じゃあ、待って...
M:-何を待つ必要がありますか?
王は、宴会テーブルから酸素カクテルを取り、肘掛け椅子に座り、ストローから数口を引いて、「見よ」と答えました。
約1時間が経過すると、観客はすでに退屈し始め、スタジアムでビールの下にビールの缶を投げ始めました。一部の人々はそこを歩いていた宇宙飛行士にさえ入ることができました...突然、スタジアムのゲートが開き、小さなトラックがロケットトレインまで行きました。 彼の体は明るい緑色に塗られており、その上にはっきりと見える半透明の緑色の泡があり、その真ん中に「緑色の泡-卸売りと小売り!」という碑文がありました。 車の外で、数人が緑色の箱を運んでロケット列車に引きずり込んで......
M:-これらのバブルは何ですか?
K:-これらは覆面捜査官であり、政府のために働いています...
M:-それにエージェントは何をするの?
K:-私は急進的な措置を取り、あなたに私の最後の議論を与えることにしました...王の最後の議論...あなたが反対することはできません...
M:(少し驚いた声で)-私たちの意見のために刑務所に送られますか?
K:-いや、いや、もちろん...あなた自身があなたの運命を選ぶ。
M:-どんな意味で?
K:-ISOによって生成された多くのユニバースとその時間と空間に関して、エラーを最小限に抑えることにしました。
K:-あなたが見たエージェントは電車に爆弾を積み込み、電車の中央にあるセンサーに接続しました。 センサーは、列車の始点と終点からの2つの光線の同時到着を修正する場合にのみ、爆弾をトリガーしてオンにするようにプログラムされています。
K:「今、電車を立ち上げます。今のところ、答えてみてください。目的地に到着するか、途中で爆発しますか?」
K:「私の忠実な助手、ダルタニャンはすでに電車の到着場所にいます。彼はすぐに戻ってきて、電車を見たら知らせます。
うーん、しかし、あなたの選択は大きくありません、2つのオプションだけがあります、そして、両方ともサービスステーションと矛盾します!
1. ISOプラットフォームに関しては、センサーへの光線の到着は同時ではなく、列車は爆発しません。
2.動いている列車のISOに関しては、センサーへの光線の到着は同時であり、列車は爆発します。
列車が爆発しない場合、プラットフォームISOは移動する列車のISOよりも利点(センサーに決定的な影響)を持ち、爆発する場合は反対になります。 つまり いずれにせよ、ISOの一部は等しくありません。これは、SRTの第1の前提に対する直接の矛盾です。SRTは、宇宙に割り当てられたISOはなく、すべてのISOが等しいと述べています。
K:-それで、電車は目的地に到着するのでしょうか... ダルタニャンはどのようなレポートで戻ってきますか?
まあ、それがすべてです。 この読書を楽しんで、王様の最後の質問に答えてくれたらと思います。 時計を見ると、世界の終わりがすでに来ていることがわかります... 2012年2月21日に記事を公開することは象徴的ですが、この世界の速度を制限します...しかし、その時点では通常のデザインがなく、ドラフトコピーでほこりっぽくなりました...
それでは、列車のロケットを発射して、実際に何が起こるかを見てみましょう。
私は王の従者ほど速くはありません。一晩でロケット列車を作成するのは現実的ではありません。数日かかりました... STOユニバースをモデル化し、方程式を使用して船の動きを説明するプログラムのソースコード(IDE C ++ Builder 2007) 。 今、私は、ピタゴラスの定理を証明した古代の数学者のように、たった1つの単語「Look!」で証明にコメントすることができます...しかし、21世紀では、3つの単語がより関連します:
実験1
プログラムでは「単純な動き」と呼ばれ、何かに反論するという目標を設定しません。 仕事は、STO宇宙の列車の単純で直線的な動きが、静止した観測者と列車にいる観測者の目を通してどのように見えるかを確認することです。 コンピューターモデルでは、オブジェクトの周囲の色付きの四角形は視覚的な視覚化のためだけのものであり、実際、オブジェクトはこれらの四角形の中央にある点に注意する必要があります。
主なものとして、固定のISO Kが選択され、これに関連して列車が移動します。 さらに、あるISOから別のISOに座標を変換することにより、列車に関連付けられたISO Kにあるポイントが計算されました。
オブジェクトの座標を取得するために使用された方程式は次のとおりです。
1.固定ISOのポイントの動き
x = x0 + v * t;
x-固定ISOのポイントの現在のx座標
x0-固定ISOのポイントの初期x座標
vは、固定ISOのポイントの速度です。
t-固定ISOのポイントの現在時刻
ここで、tはプログラムで指定されたステップによって異なり、指定されたtに対応するxを生成します。
2.動くISOで座標を取得する
ここに
相対論的速度加算として計算されたout_obj.v
out_obj.tは、実験の開始から経過した相対論的な時間間隔として計算されます
out_obj.xは、式x '= x0' + v '* t'によって計算されます。 移動するISOに対して既に計算された座標に従って
KからK 'への座標変換関数の完全なリスト:
//--------------------------------------------------------------------------- // abs - x t // t_move_abs: x = x0 + v * t //--------------------------------------------------------------------------- void __fastcall MMatPoint::MoveAbsFormula ( const double in_new_time // t ) { // x – x // x0 – x // v – // t – t = in_new_time; x = x0 + v * t; } 2. K’ K m , K K’ ( , vv mm): //--------------------------------------------------------------------------- // //--------------------------------------------------------------------------- void __fastcall MMatPoint::TransformStoFormula ( const double in_move_v, // MMatPoint& out_obj // ) { // const double& m = in_move_v; double mm = m * m; double cc = g_light_c * g_light_c; try { // v' = // K ==> K' out_obj.v = (v - m) / (1 - (v * m)/cc); } catch(...){} try { // t' = // K ==> K' out_obj.t = t * sqrt(1 - (mm)/(cc)); } catch(...){} try { // x0' = // K ==> K' double x00 = (x0) / sqrt(1 - (mm)/(cc)); // x' K' // x' = x0' + (v' * t') out_obj.x = x00 + out_obj.v * out_obj.t; } catch(...){} AnsiString dbg; dbg.printf("[%s (x=%0.2f, v=%0.2f, t=%0.2f)] ==> [%s (x=%0.2f, v=%0.2f, t=%0.2f)]", name, x, v, t, out_obj.name, out_obj.x, out_obj.v, out_obj.t); frmMain->m_Memo_Dbg->Lines->Add(dbg); }
, …

. Ex1_t0.
t=0 ( ):
:
— = 30
v – (. A1, As, A2) = 20 (2/3c)
x – , (.. — A2, 2(240), As(120), A1(0))
t — = 0 (.. 0)
:
— = 30
v’ – (. A1’, As’, A2’) = 0
x’ – 2’(321.99), As’(161), A1’(0)
t’ — = 0 (.. 0)
[A2 (x=240.00, v=20.00, t=0.00)] ==> [A2' (x=321.99, v=0.00, t=0.00)]
[As (x=120.00, v=20.00, t=0.00)] ==> [As' (x=161.00, v=0.00, t=0.00)]
[A1 (x=0.00, v=20.00, t=0.00)] ==> [A1' (x=0.00, v=0.00, t=0.00)]
.. : K’ (A2’ — A1’) = 321.99, K (A2 — A1) = 240. .. , K’ K.

. Ex1_t10.
t — = 10 (.. 10)
[A2 (x=440.00, v=20.00, t=10.00)] ==> [A2' (x=321.99, v=0.00, t=7.45)]
[As (x=320.00, v=20.00, t=10.00)] ==> [As' (x=161.00, v=0.00, t=7.45)]
[A1 (x=200.00, v=20.00, t=10.00)] ==> [A1' (x=0.00, v=0.00, t=7.45)]
t (- ): K t=10, K’ t’=7.45. , K’ K, t’ 2,55 .
2.
: « ( — )»
. 1 : F1 F2 ( ) – . D1 ( ) – , , .
, , , (A1,A2; A1’,A2’) (F1,F2; F1’,F2’).

. Ex2_t0.
t=0: . A1-F1, A2-F2, A1’-F1’, A2’-F2’ , .. .
[D1 (x=120.00, v=20.00, t=0.00)] ==> [D1' (x=161.00, v=0.00, t=0.00)]
[A2 (x=240.00, v=20.00, t=0.00)] ==> [A2' (x=321.99, v=0.00, t=0.00)]
[As (x=120.00, v=20.00, t=0.00)] ==> [As' (x=161.00, v=0.00, t=0.00)]
[A1 (x=0.00, v=20.00, t=0.00)] ==> [A1' (x=0.00, v=0.00, t=0.00)]
[F2 (x=240.00, v=-30.00, t=0.00)] ==> [F2' (x=321.99, v=-30.00, t=0.00)]
[F1 (x=0.00, v=30.00, t=0.00)] ==> [F1' (x=0.00, v=30.00, t=0.00)]

. Ex2_t1.40.
t=1.40: . , K F1-D1 > F2-D2, K’ F1’-D1’ = F2’-D2’
[D1 (x=148.00, v=20.00, t=1.40)] ==> [D1' (x=161.00, v=0.00, t=1.04)]
[A2 (x=268.00, v=20.00, t=1.40)] ==> [A2' (x=321.99, v=0.00, t=1.04)]
[As (x=148.00, v=20.00, t=1.40)] ==> [As' (x=161.00, v=0.00, t=1.04)]
[A1 (x=28.00, v=20.00, t=1.40)] ==> [A1' (x=0.00, v=0.00, t=1.04)]
[F2 (x=198.00, v=-30.00, t=1.40)] ==> [F2' (x=290.69, v=-30.00, t=1.04)]
[F1 (x=42.00, v=30.00, t=1.40)] ==> [F1' (x=31.30, v=30.00, t=1.04)]

. Ex2_t2.40.
t2.40: , K, F2 D1 F2 – . , ! ’, , .
[D1 (x=168.00, v=20.00, t=2.40)] ==> [D1' (x=161.00, v=0.00, t=1.79)]
[A2 (x=288.00, v=20.00, t=2.40)] ==> [A2' (x=321.99, v=0.00, t=1.79)]
[As (x=168.00, v=20.00, t=2.40)] ==> [As' (x=161.00, v=0.00, t=1.79)]
[A1 (x=48.00, v=20.00, t=2.40)] ==> [A1' (x=0.00, v=0.00, t=1.79)]
[F2 (x=168.00, v=-30.00, t=2.40)] ==> [F2' (x=268.33, v=-30.00, t=1.79)]
[F1 (x=72.00, v=30.00, t=2.40)] ==> [F1' (x=53.67, v=30.00, t=1.79)]

. Ex2_t7.20.
t=7.20: , K’, F2’ D1’ F2’ – . , , … . ’, , .
[D1 (x=264.00, v=20.00, t=7.20)] ==> [D1' (x=161.00, v=0.00, t=5.37)]
[A2 (x=384.00, v=20.00, t=7.20)] ==> [A2' (x=321.99, v=0.00, t=5.37)]
[As (x=264.00, v=20.00, t=7.20)] ==> [As' (x=161.00, v=0.00, t=5.37)]
[A1 (x=144.00, v=20.00, t=7.20)] ==> [A1' (x=0.00, v=0.00, t=5.37)]
[F2 (x=24.00, v=-30.00, t=7.20)] ==> [F2' (x=161.00, v=-30.00, t=5.37)]
[F1 (x=216.00, v=30.00, t=7.20)] ==> [F1' (x=161.00, v=30.00, t=5.37)]

. Ex2_t12.
t=12.00: , , K, ( K’ ) F1 - D1.
[D1 (x=360.00, v=20.00, t=12.00)] ==> [D1' (x=161.00, v=0.00, t=8.94)]
[A2 (x=480.00, v=20.00, t=12.00)] ==> [A2' (x=321.99, v=0.00, t=8.94)]
[As (x=360.00, v=20.00, t=12.00)] ==> [As' (x=161.00, v=0.00, t=8.94)]
[A1 (x=240.00, v=20.00, t=12.00)] ==> [A1' (x=0.00, v=0.00, t=8.94)]
[F2 (x=-120.00, v=-30.00, t=12.00)] ==> [F2' (x=53.67, v=-30.00, t=8.94)]
[F1 (x=360.00, v=30.00, t=12.00)] ==> [F1' (x=268.33, v=30.00, t=8.94)]
:
’, ?
– .
. – – , . (), . . - , , , , – .
, v = 0,1;
. 0,1 / 30 = 0,003333 , ! , , v = 0,003333 * = 0,003333 * 300000 = 1000 / !!! 10 = 1/30c = 10000 /… , .
, , :
№1. ( ):
...
« - ,
. ,
,
, «».
, ,
- ,
. , , : « 7 »,—
: «
7 ».
, ,
«», , «»
« ». , ,
, ,
, ;
, ,
, , ,
, ,
, .»
. ,
,
, «».
, ,
- ,
. , , : « 7 »,—
: «
7 ».
, ,
«», , «»
« ». , ,
, ,
, ;
, ,
, , ,
, ,
, .»
— . , , , , . , , () (/).
№2. – ( ):
...
« A , ,
A,
A
. B (
: « , A»),
B B .
- A B; «A-»
«B-», A B «». ,
, «», A B,
«», B A.
tA «A-» A B, tB «B-
» B A A t'A «A-».
A B , , , tB — tA = t'A – tB.
,
,
, :.
1) B A, A
B;
2) A B, C,
B C .
, ()
, , ,
, ,
, : «» «».
«» —
,
,
.
,
: ,
, « ».»
A,
A
. B (
: « , A»),
B B .
- A B; «A-»
«B-», A B «». ,
, «», A B,
«», B A.
tA «A-» A B, tB «B-
» B A A t'A «A-».
A B , , , tB — tA = t'A – tB.
,
,
, :.
1) B A, A
B;
2) A B, C,
B C .
, ()
, , ,
, ,
, : «» «».
«» —
,
,
.
,
: ,
, « ».»
— . , .
№3. . ( ):
...
«
V .
( ), . , , . .
(, ), , ? , .
, , : , , . B . ’ . ’ ( ) , , , V. , ’ , , , . . . ( ) , , , . , . , , , , , . .
, , , ( ). ( ) . , , .
»
V .
( ), . , , . .
(, ), , ? , .
, , : , , . B . ’ . ’ ( ) , , , V. , ’ , , , . . . ( ) , , , . , . , , , , , . .
, , , ( ). ( ) . , , .
»
— .
’ ( )?
A B, ’, (), A B, !
, ( ) ( ). . -, , .
, « ’ ( ) », A’ B’ / ( ).
A’ B’ ( ) , (.. – , , ) ( ) ( ). , , ( ), , . , M’, , « » .
, : «, , , ( ).» — !
, , ( ) / , , , .
:
, , , ( , ).
, :
« », , . , , , « » , .
:
2 : « » — . 1 : « » , 1 () 2 (/ ) , – .
…
’ , - , . , . , , ’ -, - .
PS:
, , , . , , «» , , . , , , . , .
. 1.
(++Builder 2007) , exe Windows .
.
, – , .
,
(free_mind2@list.ru)

, , . , , .
. .
, , , 2 . ( )
,
:
, - , .
, , :
0. 1 2 2, 2 ( , )
1. , , (=, =+) , ± 1 ( , , )
2. 1 2 , ( 6:00) ( 1) 1 2 .
3. 1 2 T=2/. , 1 : T = / , = =+=2, C+C=2 ( ) C ( ), +=2 №0. , : (V12) = (V1+V2) / (1 + (V1*V2)/C^2), V1=C, V2=C, V12 = (C+C) / (1 + (C*C)/C^2) = 2C / 2 = C, .. 1 2 C. T = / = 2 / .
4. , , 1 1 = / C. , 1 , 3: T = / , = , +V, V=0, , .. +0 = (.. 1). , : (V12) = (V1+V2) / (1 + (V1*V2)/C^2), V1=C, V2=0, V12 = (C+0) / (1 + (C*0)/C^2) = C / 1 = C, .. 1 1 C. 1 T = / = / .
5. 1 2 (.. =) = (.. 1 2 1 )
6. , T = 2/, = /, = , .. 2/ != /, != , 5!!! , (1) T=2/ >> T=/ != .
7. , , !
8. , 1 1 2 ( ) . 1 ( ) , T ( 2 ). , , C+C=C. , +=2, (T=2/2C=/, =/, = )
9. , 1 , ! (.. )
10. ?
, - , .
, , :
0. 1 2 2, 2 ( , )
1. , , (=, =+) , ± 1 ( , , )
2. 1 2 , ( 6:00) ( 1) 1 2 .
3. 1 2 T=2/. , 1 : T = / , = =+=2, C+C=2 ( ) C ( ), +=2 №0. , : (V12) = (V1+V2) / (1 + (V1*V2)/C^2), V1=C, V2=C, V12 = (C+C) / (1 + (C*C)/C^2) = 2C / 2 = C, .. 1 2 C. T = / = 2 / .
4. , , 1 1 = / C. , 1 , 3: T = / , = , +V, V=0, , .. +0 = (.. 1). , : (V12) = (V1+V2) / (1 + (V1*V2)/C^2), V1=C, V2=0, V12 = (C+0) / (1 + (C*0)/C^2) = C / 1 = C, .. 1 1 C. 1 T = / = / .
5. 1 2 (.. =) = (.. 1 2 1 )
6. , T = 2/, = /, = , .. 2/ != /, != , 5!!! , (1) T=2/ >> T=/ != .
7. , , !
8. , 1 1 2 ( ) . 1 ( ) , T ( 2 ). , , C+C=C. , +=2, (T=2/2C=/, =/, = )
9. , 1 , ! (.. )
10. ?
, .
1
, .
2
C .
( , , 2 ( ), 1 ( ). .. C=const , C+V=C)
« »:
, , , () .
:
, ( , , t ), , …
, , :
« , , , , .. , ».
– . , , , .

:
1. ( C, 0). -, .
2. - , , T=/.
3. , . - . 2 , 1) , T ( , - ), , (.. T, T).
4. « », -, « ?». , , , ! , - , , , ( ), «» ( ). - , , , .

, -, . - , , , , .
, , , . ’ -: « - , , ?». , , C+C<>2C, C+C=C, : « ». «», ’, :
1. , , T = / , . T=/C. , , , , , .. , .
2. , , , (.. ) T = / , = =+=2, C+C C, . T=2/. , , , , .
3. , ( ) . T=/C T=2/C, .. /C = 2/C. , ! 1 , .
4. , , , , .
:
— , , , , — , — , . . .. - , ( ).
:
, – , , , . , , , , . () , , , , , . , . , , 12 ( ), , , () . , «» , lib.rus.ec/b/300909/read ( ), , , , .
, , :
1 , 2 , ( ) , . , .. ( ). ? , , 1 ?
:
3 , , . , ( 6:00 ) . . .. , , , .
, , , , ( ):
1.
2.
3. , =/
4.
5.
6. , +-1, T=2/ >> T=/
, , - , .
T = / ( 5 ), = =+=2, C+C C (.. C+C=2C), . T=2/
T=2/ >> T=/ :
T = /
1…
= , = +0 ( )
2. 2 (, , ! , )
= =+=2, C+C C (.. C+C=2C), . T=2/
T=2/ >> T=/!
= + = 2C, 2:
C .
( , , 2 ( ), 1 ( ). .. C=const , C+V=C) C.
— 1/ :) — :
— . /, , . =/=/=2/2.
1. , , .
2. ?( , )
T = / . (.. )
:
= =+=2, C+C C (.. C+C=2C), . T=2/, 2, , T = 2A/(C+C) = 2/2 = AB/C ( 1 ),
, C+C=2C, C+C=C.
:
, - , 2 2 2 , - 2 .
, C+C=2C ( , = 2 ( , )) 1C, ...
, , <= 2, , 2, .. — , . :
() = 2C, , , 2 2. : = v1+v2, v2 = — v1, .. 1 v1=0, v2( 2 ) = — 0, .. v2 = 2C — 0 = 2C! .. , = 2C — 2. , , 1 2 ( ), …
(V12) = (V1+V2) / (1 + (V1*V2)/C^2), V2, V2 = (V12 *^2 — V1*C^2) / (C^2 — V12*V1)
: (V12) = 2, V1=0
V2 = (2C*C^2 — 0*C^2) / (C^2 — 2C*0) = (2C*C^2) / C^2 = 2C! . .. , = 2C — 2