過去6か月で、いくつかの単純な（ルールの意味で）幾分似たボードゲームに精通することができました。 このシリーズの最初はSetで、次にLambで、夏にはDobbleをプレイしました。 これらのゲームはすべて非常にエキサイティングなものであるとすぐに言わなければなりませんが、もちろん、この投稿はそれについてではなく、議論されます。 実際、しばらくして（つまり、十分にプレイした後）、これらのゲームの根底にあるアイデアに興味があり、組み合わせ論と正確に密接に関係していることがわかりました。 この投稿では、（私の意見では）最も単純なゲームである「ラム」について説明します。これは、偶然にも、オリジナルバージョンではより調和のとれた名前「Geistesblitz」（ドイツ語：イルミネーション）です。

ゲームのルール

だからゲームは何ですか。 白いドラム、赤い椅子、青い本、緑のボトル、灰色のマウスという5つのオブジェクトがあり、それぞれがその形状と色（つまり、2つのカテゴリ）によって特徴づけられています。











さらに、多くのカードがあり、それぞれに2つのオブジェクトが描かれ、異なる形状と異なる色を持っています（ただし、上記の形状と色から）。 一部のカードには、実際のアイテムと完全に一致するアイテムがあります。 少なくとも1つのアイテムのカードで、色が形状と一致しません（たとえば、赤いボトル）。







ゲームの目標は、特定のカードについて、できるだけ早く、a）カード上に正しい形で存在する（形状と色が一致する）、b）完全に存在しない（カード上にこのオブジェクトの形がない、または色）。











最初の例では、白いドラムがあり、それをつかむ必要があります。2番目の例では、ボトルに（形状として）ボトルがなく、緑色がありません（この場合、ボトルが唯一のオプションであることを確認するのは簡単です）。残りのすべてのアイテムの個別のカテゴリがカードに存在するため）。



実際、すべてのルール。 ゲーム自体は複数のプレイヤー向けに設計されており、それぞれが自分でプレイします。目標は、できるだけ多くのカードを収集することです（最初に正しいアイテムを手に入れた人がカードです）。 注意：長い爪を持つ人とはプレイしないでください。刺し傷を負う可能性があります！

カードの数

私が興味を持った最初の質問は、このゲームでいくつのカードが可能なのかということでした。 純粋な組み合わせ論！ すばらしいことは、この問題は非常に簡単に解決されることです。 まず、2種類のカードがあることに注意してください。それらを正しい （ 正しいアイテムがある）と間違っている （そのようなカードには必要なアイテムはありません）と呼びましょう。 それらとその他の数を別々に計算します。



正しいものから始めましょう。 正しいカードの最初のアイテムは、5つの方法（5つの使用可能なアイテムのうち）で選択できます。 2番目のアイテムはより巧妙に選択されます-最初にその形状（4つのオプション、1つの形状はすでに最初のアイテムで占められています）、次に色（3つのオプション、1つの色は最初のアイテムで占められ、2番目は2番目のステップでフォームを取得したアイテムで占められます）を選択します したがって、 製品のルールに従って、正しいカードの合計数5 * 4 * 3 = 60を取得します。



間違ったカードも同様に考慮されます。 最初に、最初のアイテムの形状（5つのオプション）を選択し、次にその色（4つのオプション）を選択します。 次に、2番目のアイテムの形状（3つのオプション）とその色（2つのオプション）を選択します。 このカードの目的である、チャレンジされていないアイテムが1つだけ残っています。 製品ルールを適用し、5 * 4 * 3 * 2 = 120オプションを取得します。 しかし、これは間違った答えです。カード上のアイテムのセットが乱れているため、注文したセットの数を計算しました。 正しい答えを得るには、120を2で割る必要があります-2つの要素の順列の数（「赤いボトルと白い椅子」カード=「白い椅子と赤いボトル」カード）。 したがって、120/2 = 60の間違ったカードを取得します。



要約して（つまり、合計の規則を適用して）答えを得る：ゲームの120枚のカード。 ゲームではカードを数えます-60枚。 計算のエラー、または不足。 簡単な調査により、不足の事実が示されました。5つのアイテムのそれぞれについて、6枚の正しいカードと6枚の間違ったカードがあり、12と12があります。

一般化

問題をわずかに再定式化します。 N個のオブジェクトがあり、それぞれがk個のカテゴリで記述され、それぞれにn個のオブジェクトが描かれたQカードがあります（上記の場合、N = 5、k = 2、n = 2およびQ = 120）。 制限があります-カードは（上記の意味で）正しい場合と正しくない場合があります。 いずれにせよ、各カードでは、kNの可能性のある兆候のいずれも繰り返されません（たとえば、すべての色が異なり、すべてのフォームが異なります）。 さらに、各アイテムはカードに完全に描かれているか、属性が1つしかありません。たとえば、「ドラム」には、白いボトルと赤いドラム（1つのオブジェクトから2つの標識）のあるカードはありません。 そのようなカードには、灰色のマウスと青い本の2つの選択肢があります。 このような一般化された定式化で生じる唯一かつ自然な問題は、変数N、k、n、およびQの間の関係は何ですか？



まず、N、k、nがどのように関連しているかを簡単に確認できます。 間違ったカードを検討してください。 このようなカードにはそれぞれn個のオブジェクトが含まれています。つまり、knオブジェクトを決定するknサインが​​正確にあります（すべてのサインは異なり、2つは同じオブジェクトに属しません）。 このようなカードは含まれていない単一のアイテムに対応する必要があるため、必要なアイテム数kn + 1を取得します。 この番号を使用すると、正しいカードを作成することもできます（各正しいカードには、何らかの形式で1+（n-1）k個のアイテムがあります）。 したがって、N = kn + 1です。 上記のn = k = 2およびN = 5の場合に、式が有効であることを確認するのは簡単です。 テーブルの形で見つかった依存関係を想像してください（ゲーム「ラム」に対応するセルは赤で強調表示されます）。







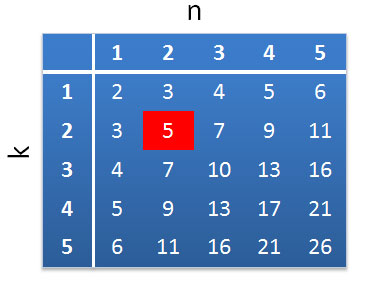
これらの数字はどういう意味ですか？ ゲームの拡張（超複雑）バージョンを作成するとします。このバージョンでは、各カードにn = 5個のアイテムがあり、各アイテムはk = 5カテゴリで記述されます。 N = 26になります。 これは、各カテゴリに対して26個の値（属性）を作成する必要があることを意味します。 つまり カテゴリが色の場合、互いに大きく異なる26色を識別する必要があります。 これは簡単な作業ではありません...したがって、可能なゲーム拡張機能は、テーブルの左上隅付近の領域に限定される可能性が高いです。 ちなみに、n = 1またはk = 1の見かけ上些細なケースにも生命権があります（ただし、これらのケースでは、主なことは良い反応になります）。



ゲームの拡張（パラメーター化）バージョンのQカードの数を計算します。 上記の手法を使用して、正しいカードの数N！/ K！/（N-1）！を見つけます。 間違ったカードの数N！/ n！、追加および単純化、結果が得られます



。



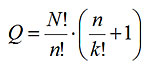この式はn = k = 2で機能し、これらのパラメーターのより低い値についてもテストされています。 確かに、n = k = 1の場合、わずかに嘘をついています。 この場合、1つのアイテムの正しいカードが別のアイテムの間違ったカードと一致する（つまり、選択が勝つ）ため、結果を2で割る必要があります。他のすべてのケースでは、このような衝突は発生しません。 n = k = 3の場合、式は数Q = 907200を与えます。 各カードの厚さが10分の1ミリメートルの場合、スタック全体の高さはほぼ90メートルになります。

ケースn = k = 3の実現

キッチン全体を把握した後、nとkの1から3までのすべての値について、ゲームの拡張バージョンの簡単なプロトタイプデモを作成することにしました。しかし、プログラミング自体に関しては、私の熱意はわずかに落ち着き、ケースに限定することにしましたn = k = 3（N = 10）。 これは記事の単なるデモンストレーションであるため、グラフィックスに煩わされるのではなく、ゲームのほぼテキストバージョンを作成することにしました。 したがって、3つのカテゴリは文字（AからJ）、数字（0から9-10進数システムがあることは非常に幸運です）、特殊文字（パーセント、ドルなど）です。したがって、各「アイテム」 A0％、B1 $などの3文字（文字+数字+特殊文字）のセット（順不同）です。 ゲームは物事を推測するために100秒を与えられている一人のプレイヤーのために設計されています。 アイテムを正しく選択すると、スコアに1が加算され、間違ったアイテムを選択するとスコアが1減ります（ただし、ゼロになるだけです）。 ゲームはHTML + JSで実装されており、 ここに投稿されています （Chromeでのみテスト済み）。 インターフェイスは非常にシンプルです。







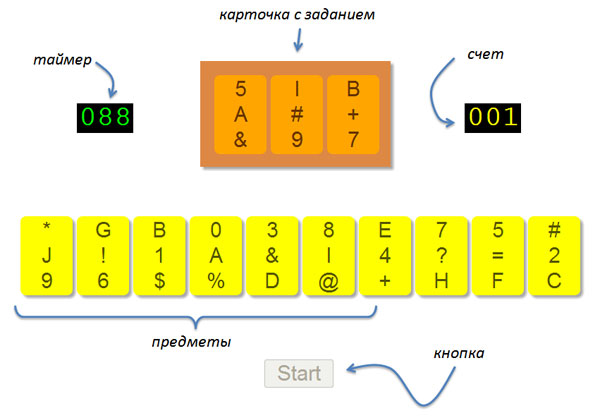
3つのオブジェクトを持つカードが上段に表示され、下段にオブジェクト自体があります。 下の行から、カード上にあるオブジェクト（3文字すべてが一致する）、またはカード上の単一のシンボルではないオブジェクトを選択する必要があります。 この例では、正しい選択は文字Gのカードです。ゲームを複雑にするために、少し難読化（「オブジェクト」に「オブジェクト」とシンボルを混合）を使用しています。 「ラム」の元のバージョンも難読化されていることに注意してください-オブジェクトはサイズが異なり、さまざまな方法でカードに配置されます（さらに、ゲーム中に実際のオブジェクトはプレイヤー自身によって常に混合されます）。 あえてプレイする人たちに幸運を祈ります（これまでの私の記録は約6個の推測アイテムです）！



ご清聴ありがとうございました！



PS：そして、直交多項式はそれと何の関係があるのか​​、注意深い読者は尋ねます。 正直なところ、わかりません！ しかし、Qの式を取り、それにk = 2を代入すると、1、9、120、2100などのように始まる数値シーケンスが得られます。 このような素晴らしいサイトがあります -整数シーケンスの辞書。シーケンスのいくつかの要素（ゲーム「Guess the melody」など）を使用してシーケンス自体を見つけることができます。 そこで見つけた数字を運転しましたが、直交多項式の係数と正確に関連している唯一のシーケンスが見つかりました...テストでは、式（鉱山とそれら）が同一であることが示されました。 私は怠theすぎず、元の記事を見つけてダウンロードしました。私の数値は、逆ラプラス変換の過程で何らかの方法で得られた多項式で3番目に古い係数であることが判明しました 。 残念ながら、これらの多項式と「ラム」の関係は理解できませんでした...