準同型暗号化は、暗号化されたテキストで操作を実行することにより、クリアテキストで特定の数学的操作を実行できる暗号化システムです。
長い間、世界のすべての暗号学者にとって、完全に準同型の暗号システムは、達成不可能な理想である聖杯でした。 そして2009年に、クレイグジェントリーは彼の論文で初めて、準同型暗号化の完全に機能するスキームを説明しました。
Gentryのアイデアの数学的詳細とそのアルゴリズムの実装例は、猫の下にあります。
準同型暗号化。
標準の暗号化システムは、3つのアルゴリズムで記述できます。
- KeyGen()キー生成
- 暗号化暗号()
- 解読()
上記の3つのアルゴリズムに加えて、準同型暗号システムにはEval()計算アルゴリズムが含まれています。
概略的に、 Evalアルゴリズムは次のように表すことができます。
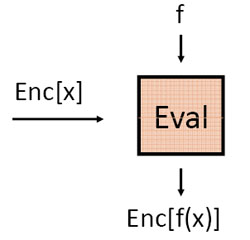
暗号化されたメッセージEnc(M)と数学関数f()がアルゴリズムに入力されます。 アルゴリズムの結果は、別の暗号化されたメッセージEnc(M 2 )であり、 M 2 = f(M)です。
準同型暗号化スキームは、キーペアSK、PK、関数f() 、暗号文セットC = {c 1 、c 2 、..、c n }および平文セットM = {m 1 、 C = Enc(M)となるm 2 、..、m n }次の条件が満たされます。
r = Eval(PK、C、f)の場合、 decypt(SK、r)= f(m 1 、m 2 、..、m n )
Gentryによって提案されたスキームはこの条件を満たすため、完全に準同型と呼ぶことができます。
番号付きのジェントリースキーム
数値形式で提示されるデータに適用可能な暗号化スキーム自体について説明しましょう。
Keygen
秘密鍵:大きい偶数N
公開鍵:a i mod N = 2e iであるような大きな数のセット{a 1 、a 2 、..、a i } 、ここでe iの数はNよりはるかに小さい。
暗号化
公開鍵から、乱数b = random-subset-sum {a i }を生成します。 1ビットの情報m∈{0,1}を暗号化するために、計算します
C = b + m
解読する
復号化のために、計算します
C mod N = m + 2 * P e i
2 * e iはノイズと呼ばれ、計算プロセスのこの式が数Nを超えると、復号化は不可能になります。
2を法として、元のメッセージmを取得します。
評価
暗号化された要素を復号化せずに追加または乗算するには、単に暗号文を追加または乗算するだけで十分です。
このスキームは完全に機能しているという事実にもかかわらず、あまり興味深いものではありません。 これを使用すると、1ビットの情報のみを暗号化できます。 大きな数を扱うために、アルゴリズムをわずかに変更します。
15以下の数字を暗号化できるスキームを構築します。
Keygen
秘密鍵: GCD(N、15)= 1のような大きな数N。
公開鍵:a i mod N = 15e iのような大きな数字のセット{a 1 、a 2 、..、a i }。ここでe iの数字はNよりはるかに小さい。
暗号化
公開鍵から、乱数b = random-subset-sum {a i }を生成します。 0から15までの数字を暗号化するために、計算します
C = b + m
解読する
復号化のために、計算します
C mod N = m + 15 * P e i
15を法としてキャストした後、元のメッセージmを取得します。
C#実装
以下は、キー生成、暗号化、および復号化機能を含むコードです。
// , k- // private BigInteger[] PublicKeyGenerate(BigInteger N, int k) { Random r = new Random(); byte[] rand = new byte[16]; BigInteger rem; for (int i = 0; i < 100; i++) { r.NextBytes(rand); PK[i] = new BigInteger(rand); PK[i] = (BigInteger.Abs(PK[i]) * N) + (k* r.Next(10, 100)); rem = BigInteger.Remainder(PK[i], N);; } return PK; } // , // M PK private BigInteger Encryption(BigInteger M, BigInteger[] PK) { BigInteger B = new BigInteger(0); BigInteger C = new BigInteger(0); Random r = new Random(); for (int i = 0; i < 100; i++) { if (r.Next(2) == 1) B = B + PK[i]; } C = M + B; return C; } // , C-, N- , //k- private BigInteger Decryption(BigInteger C, BigInteger N, int k) { BigInteger M = new BigInteger(0); M = BigInteger.Remainder(C, N); return BigInteger.Remainder(M, k); }
ここから最大1000の数字の暗号化を実装するプログラムのソースをダウンロードできます。
おわりに
結論として、このトピックで説明されている暗号システムはプロトタイプにすぎず、その主な目的は、準同型暗号システムの動作原理に興味がある人に慣れることです。 実際の準同型スキームは整数では機能しませんが、多項式リングでは機能します。また、各計算の後にモジュロを減らしてノイズを減らし、復号化が不可能にならないようにします。