👩🏽 📸 📶 バイナリ検索を書くことができません 💠 🌓 👇🏼

最近（文字通り2年前）、ある記事がここを通り抜けました。バイナリ検索を記述できるのはプログラマの10％だけです。バイナリ検索は、 古典的な検索アルゴリズムです。さらに、これは非常に簡単に説明できる非常に単純なアルゴリズムです。ソートされた配列を取得し、中間にあるものに応じて番号が見つからない場合は中央を見てください-左側または同じ方法でこの番号を探します、または右側で、中央の要素をリクライニングします。関数についても、配列ではなく関数を取ります。すべてが非常に非常に単純であり、アルゴリズムはほぼどこでも記述されており、すべてのバグがキャッチされて記述されています。

そのため、バイナリ検索を実装できません。私にとって、彼はささいなことではありません。私は偽のプログラマーだと思います。しかし、それは、私はただの学生ですが、これは言い訳ではありませんか？もっと正確に言えば、私は良い正しい美しいバイナリ検索を実装することはできません。私は常に、正確さ、可愛さ、またはその両方で問題を抱えています。それで、はい、タイトルは少し黄色がかっています。

このトピックを読む前に、ソート済み配列のバイナリ検索のバージョンを作成してください。さらに、パラメータに応じて、検索は最初の要素または重複のいずれかを返す必要があります。比較のために、関数のバイナリ検索を記述します

まず、C＃でコードを記述します。他の言語のファンが私のコードを簡単に理解できることを願っています。検索の境界を半間隔として表します[左; 右）、つまり左のポイントがオンになり、右のポイントがオフになります。半分の間隔は私にとってより便利です。私はすでにその動作に慣れています。さらに、さまざまなアルゴリズムをプログラミングするときに、半分の間隔を使用するといくつかの利点があります（これについては後で説明します）。一般に、次のようなループを記述するため、「統一プログラミングスタイル」をサポートするという点では、半間隔を使用する方が適切です。

for (int i = 0; i < array.Length; i++)

for (int i = 0; i <= array.Length - 1; i++)

, , . :

static int BinarySearch_Rec_Wrapper(int[] array, int element)
{
    BinarySearch_Rec(array, element, 0, array.Length);
}

, . , . , ,

int mid = (left + right) / 2

, (. ):

 int mid = left + (right - left) / 2

, . off-by-one. , :

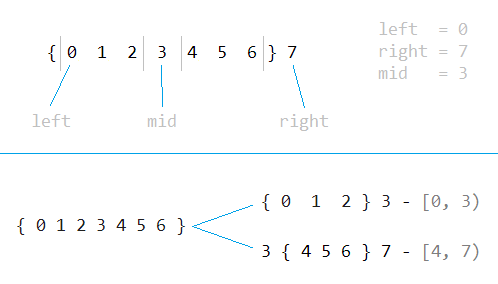
, [0, 3) [4, 7), .. [left, mid) [mid + 1, right). , «» ( ), , , , . , , , , .

, : [left, right], [left, mid — 1] [mid + 1; right] ( , , ).

1 ( , ), — 2 — , .

, ( [left, mid) [mid, right)), 1 ( [left, mid] [mid + 1, right], [left, mid — 1] [mid, right]).

, , , , (array[mid]), (key). — , , , , :-). - . , , «».

:


static int BinarySearch_Rec(int[] array, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (array[mid] == key)
        return mid;

    else if (array[mid] > key)
        return BinarySearch_Rec(array, key, left, mid);
    else
        return BinarySearch_Rec(array, key, mid + 1, right);
}

:


static int BinarySearch_Iter(int[] array, int key)
{
    int left = 0;
    int right = array.Length;

    while (true)
    {
        int mid = left + (right - left) / 2;

        if (array[mid] == key)
            return mid;

        if (array[mid] > key)
            right = mid;
        else
            left = mid + 1;
    }
}

:

, , , . while(true), , . , , . , .

, , . - , ? - . ? ( , -1)? int int? null? (int? c# — , null). , - , ? - ? … , « ?». , , : , . , , , null, null.

-(1 + left), , , , . , — , . DRY, - , . , .

, left == right, .., — [left, right). , right — left < 1 right — left <= 0. , , , - ( , ).

:


static int BinarySearch_Rec(int[] array, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (left >= right)
        return -(1 + left);

    if (array[mid] == key)
        return mid;

    else if (array[mid] > key)
        return BinarySearch_Rec(array, key, left, mid);
    else
        return BinarySearch_Rec(array, key, mid + 1, right);
}

:


static int BinarySearch_Iter(int[] array, int key)
{
    int left = 0;
    int right = array.Length;
    int mid = 0;

    while (!(left >= right))
    {
        mid = left + (right - left) / 2;

        if (array[mid] == key)
            return mid;

        if (array[mid] > key)
            right = mid;
        else
            left = mid + 1;
    }

    return -(1 + left);
}

:

, . , , . , - , .

№3

, . ||, &&, , XOR':

descendingOrder	array[mid] > key	XOR
0	0	0
0	1	1
1	0	1
1	1	0

.. descendingOrder , , , . «», , - . , .

:


static int BinarySearch_Rec(int[] array, bool descendingOrder, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (left >= right)
        return -(1 + left);

    if (array[mid] == key)
        return mid;

    else if ((array[mid] > key) ^ descendingOrder)
        return BinarySearch_Rec(array, descendingOrder, key, left, mid);
    else
        return BinarySearch_Rec(array, descendingOrder, key, mid + 1, right);
}

static int BinarySearch_Rec_Wrapper(int[] array, int key)
{
	if (array.Length == 0)
        return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Rec(array, descendingOrder, key, 0, array.Length);
}

:


static int BinarySearch_Iter(int[] array, bool descendingOrder, int key)
{
    int left = 0;
    int right = array.Length;
    int mid = 0;

    while (!(left >= right))
    {
        mid = left + (right - left) / 2;

        if (array[mid] == key)
            return mid;

        if ((array[mid] > key) ^ descendingOrder)
            right = mid;
        else
            left = mid + 1;
    }

    return -(1 + left);
}

static int BinarySearch_Iter_Wrapper(int[] array, int key)
{
	if (array.Length == 0)
    	return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Iter(array, descendingOrder, key);
}

:

: , . .

№4

, . «» — , . , , … .

, , :

, , , . , , . , , . (. )

:


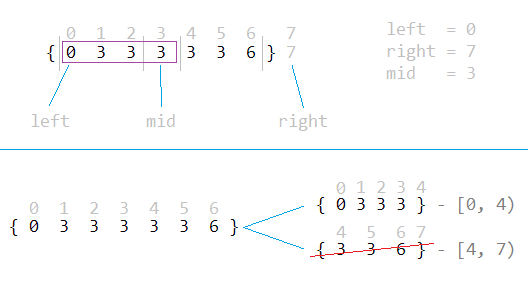
static int BinarySearch_Rec(int[] array, bool descendingOrder, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (left >= right)
        return -(1 + left);

    if (array[left] == key)
        return left;

    if (array[mid] == key)
    {
        if (mid == left + 1)
            return mid;
        else
            return BinarySearch_Rec(array, descendingOrder, key, left, mid + 1);
    }

    else if ((array[mid] > key) ^ descendingOrder)
        return BinarySearch_Rec(array, descendingOrder, key, left, mid);
    else
        return BinarySearch_Rec(array, descendingOrder, key, mid + 1, right);
}

static int BinarySearch_Rec_Wrapper(int[] array, int key)
{
    if (array.Length == 0)
        return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Rec(array, descendingOrder, key, 0, array.Length);
}

:


static int BinarySearch_Iter(int[] array, bool descendingOrder, int key)
{
    int left = 0;
    int right = array.Length;
    int mid = 0;

    while (!(left >= right))
    {
        mid = left + (right - left) / 2;

        if (array[left] == key)
            return left;

        if (array[mid] == key)
        {
            if (mid == left + 1)
                return mid;
            else
                right = mid + 1;
        }

        else if ((array[mid] > key) ^ descendingOrder)
            right = mid;
        else
            left = mid + 1;
    }

    return -(1 + left);
}

static int BinarySearch_Iter_Wrapper(int[] array, int key)
{
    if (array.Length == 0)
        return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Iter(array, descendingOrder, key);
}

№5

, , , , . , , :


enum ElementToChoose
{
	First,
	Last,
	NoCare
}

/// <summary>
/// Finds element equal to value in sorted array in range [low, high)
/// </summary>
static int binarySearch(int value, int[] array, bool ascendingOrder, ElementToChoose elementToChoose, int low, int high) {
	// return valid invalid position
	if (low >= high)
		return -(low + 1);

	// return first or last found element
	if (elementToChoose == ElementToChoose.First)
		if (value == array[low])
			return low;

	int last = high - 1;

	if (elementToChoose == ElementToChoose.Last)
		if (value == array[last])
			return last;

	int mid = low + (high - low) / 2;

	// we have found some element
	if (value == array[mid]) {
		switch (elementToChoose) {
			case ElementToChoose.NoCare:
				return mid;

			case ElementToChoose.First:
				if (mid - low <= 1)
					// array[mid] is the earliest element in array, return it
					// because array[low] != value && array[low+1] == value, where mid == low + 1
					return mid;
				else
					// try to find first element
					// don't forget to capture current element {|0, 0|, 1} -> {0, 0}
					return binarySearch(value, array, ascendingOrder, elementToChoose, low, mid + 1);
			case ElementToChoose.Last:
				if (last - mid <= 1)
					// array[mid] is the last element in array, return it
					// because array[last] != value && array[last - 1] == value, where mid == last - 1
					return mid;
				else
					// try to find last element
					// don't forget to capture current element {0, |0, 1|} -> {0, 1}
					return binarySearch(value, array, ascendingOrder, elementToChoose, mid, high);
		}
	}

	// choose left or right half, depending on sorting order & comparing value and mid
	if ((value < array[mid]) ^ !ascendingOrder)
		return binarySearch(value, array, ascendingOrder, elementToChoose, low, mid);
	else
		return binarySearch(value, array, ascendingOrder, elementToChoose, mid + 1, high);
}

, ? , 3 , ? , , , ( ).

, , / getFirstHalf, getSecondHalf ( ), getStartPoint/getLastPoint ( / ), increaseLength/decreaseLength ( ), moveStartPoint. - . , .

, , . … , « », . :


//   - Func<float, float> ,  float   float
static float BinarySearch_Func(Func<float, float> func, bool descendingOrder, float key, float left, float right)
{
    float mid = (left + right) / 2;

    if (left == mid || mid == right)
        return mid;

    if ((func(mid) > key) ^ descendingOrder)
        return BinarySearch_Func(func, descendingOrder, key, left, mid);
    else
        return BinarySearch_Func(func, descendingOrder, key, mid, right);
}

static float BinarySearch_Func_Wrapper(Func<float, float> func, float key, float left, float right)
{
    if (left > right)
        return float.NaN;

    bool descendingOrder = func(left) > func(right);
    bool isOk = true;

    if (!descendingOrder)
        isOk = func(left) <= key && key <= func(right);
    else
        isOk = func(right) <= key && key <= func(left);

    if (isOk)
        return BinarySearch_Func(func, descendingOrder, key, left, right);
    else
        return float.NaN;
}

. ? ? float'? ( , ?, , - ).

? left; right? [left, right], [left, right), (left, right], (left, right)? . :


//   x => x - -  f(x) = x
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.7f, 0.7f, 100.0f)); // : 0.7
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.8f, 0.8f, 100.0f)); // : 0,8000001
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.9f, 0.9f, 100.0f)); // : 0,9

Console.WriteLine("{0:0.00000000}",0.8f); // : 0,80000000

, left . right (). .. a b, a, b, - . .

, , , mid /. .

- , func(left) == key func(right) == key, .

, : , .

, , - . , - .

, - , : , — , a/b. : a b . -: O(lgn).

, : - — , // , , ?

P.S: , . ,

P.P.S: ?

UPD1: fox_anthony -(1 + left) ~left. : ~, msdn, c#

バイナリ検索を書くことができません

:

:

:

:

:

:

№3

:

:

:

№4

:

:

№5

More articles: