この記事の目的は、コンピューターゲーム（主に拮抗的 ）の「人工知能」を構築および最適化するための基本的な方法の本質を明らかにすることです。 うさぎとオオカミのゲームの例を使用して、Minimaxアルゴリズムとその最適化アルゴリズムAlpha Beta Cutoffを検討します。 テキストの説明に加えて、記事にはイラスト、表、ソースコード、既成のオープンソースのクロスプラットフォームゲームが含まれており、そこでインテリジェントエージェントと競うことができます。

ゲーム「ウサギとオオカミ」

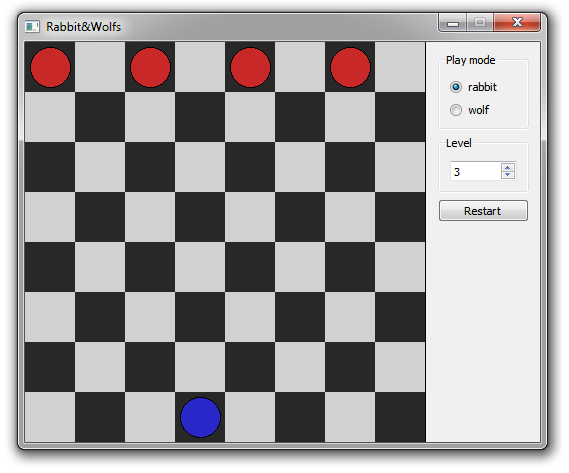
チェス盤には、上部に4匹のオオカミ（黒いセル）があり、下部に1匹のノウサギ（黒いセルの1つ）があります。 ウサギが最初に歩きます。 オオカミは下にしか行けず、ウサギはどの方向にでも行けますが、斜めに歩くことができるのは1マスだけです。 ノウサギが上部のセルの1つに到達すると勝利し、オオカミはウサギを囲んだり押したりした場合（ウサギに行く場所がない場合）に勝利します。

読み続ける前に、 演奏することをお勧めします。理解しやすいでしょう。

発見的

実用的な工学用語では、ミニマックス法は発見的手法に基づいており、アルゴリズムの本質に移る前に検討します。

ミニマックスのコンテキストでは、あらゆる州のプレイヤーの勝利の確率を評価するために、ヒューリスティックが必要です。 タスクはヒューリスティック評価関数を構築することです 。これは、選択されたメトリックで、プレーヤーがこの状態になった方法に依存することなく、特定の数字の配列で特定のプレーヤーが勝つ確率の推定値を迅速かつ正確に指定できるようにすることです。 私の例では、評価関数は0〜254の値を返します。0はうさぎの勝利、254はオオカミの勝利、中間値は上記の2つの推定値の補間です。 確率の推定は確率ではなく、制限する必要はありません、線形、連続。

評価関数の例1 。 ノウサギが高ければ高いほど、勝つチャンスが増えます。 このようなヒューリスティックは、速度の観点から効果的ですが（O（1））、アルゴリズム的には完全に不適切です。 ノウサギの「高さ」は勝利の確率と相関しますが、ノウサギの主な目標である「勝つ」を歪めます。 この評価関数は、ノウサギに上に移動するように伝えますが、計算の深さが浅い場合、障害に関係なくノウサギが上に移動し、トラップに陥ります。

評価関数の例2 。 うさぎは勝つ可能性が高く、凍ったオオカミで勝つための動きをする必要が少なくなります。 これは、複雑さO（n）のより扱いにくいアルゴリズムです。ここで、nはセルの数です。 移動数の計算は、幅優先検索になります。


ご注意 この記事で提供されるソースは、読者がメインアプリケーションのコンテキスト外でその本質を理解できるように変更されています。 記事の最後で信頼できるソースを探してください。

幅優先検索を実行するコード、またはむしろウサギから「距離」に等しい値でマップを埋めるコード：

this->queue.enqueue(this->rabbitPosition); while (!this->queue.empty()) { QPoint pos = this->queue.dequeue(); for (int i = 0; i < 4; i++) if (canMove(pos + this->possibleMoves[i])) { QPoint n = pos + this->possibleMoves[i]; this->map[ny()][nx()] = this->map[pos.y()][pos.x()] + 1; this->queue.enqueue(n); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

評価関数の結果は、最も近い上位セルまでの「距離」に等しい値、または到達できない場合は254でなければなりません。 以下で説明する欠点にもかかわらず、ゲームで使用されるのはこの経験則です。

ソースを見て理解する人のために-注意！ アプリケーションアーキテクチャは、コードの他の部分に影響を与えることなく評価関数をやり直すことができるように設計されています。 ただし、以前に選択したメトリックを使用する必要があります。そうしないと、アルゴリズムは評価関数の指示を理解しません。

ミニマックス

いくつかの概念と表記法を紹介します。

• 状態、それは決定木のノードでもあります-ボード上の数字の位置。
• 最終状態とは、それ以上の動きがない状態です（誰かが勝った/引く）。
  
• Viはi番目の状態です。
• Vikは、Vi状態から1回の移動で到達できるk番目の状態です。 決定木のコンテキストでは、これはViの子ノードです。
• f（Vi）は、州Viの勝利確率の計算された推定値です。
• g（Vi） -州Viの勝利確率の発見的推定値。

f（Vi）はg （Vi）とは異なり、 g（Vi）はViに関する情報のみを使用し、 f（Vi）はVikおよびその他の状態も再帰的に使用します。

この方法は、 Vi状態からの移動を選択する問題を解決するように設計されています。 確率推定が歩行しているプレーヤーにとって最も有益である動きを選択することは論理的です。 メトリックでは、オオカミの場合-最大評価、ノウサギの場合-最小。 そして、評価は次のように考慮されます。

• f（Vi）= g（Vi） 、 Viが最終状態の場合、または計算の深さの限界に達した場合。
• f（Vi）= max（f（Vi1）、f（Vi2）... f（Vik）） 、 Viがプレーヤーが最大スコアを探しに行く状態である場合。
• f（Vi）= min（f（Vi1）、f（Vi2）... f（Vik）） Viがプレイヤーが最小スコアを見つけるために歩く状態である場合。

この方法は常識に基づいています。 私たちは自分の勝利Pの評価を最大化するように歩きますが、少なくとも何かを計算するためには、敵の歩き方を知る必要があり、敵は彼の勝利の評価を最大化するように歩きます（P評価を最小化するため）。 言い換えれば、敵がどのように歩くかを知っており、この方法で確率推定を構築できます。 敵が同じ評価関数を持っている場合、アルゴリズムが最適であり、最適に動作することを示す時です。 この場合、インテリジェンスは誤算の深さと評価関数の品質に依存します。

例を挙げましょう。


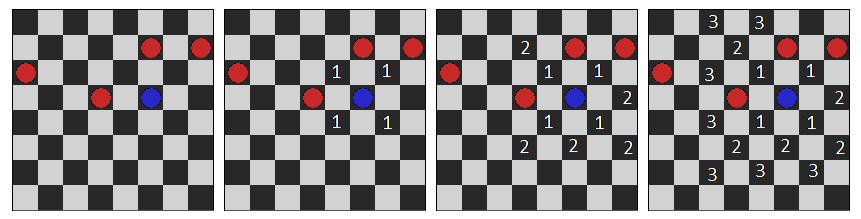
この例では、プレーヤーは野ウサギで、コンピューターはオオカミで遊んでいます。 野ウサギが歩き回った後、コンピューターはミニマックスアルゴリズムを実行します。この例では、深さ1でアルゴリズムは何をしますか？ そして誰が知っていますか？ アルゴリズムはオオカミのすべての可能な動きを通過し、彼らのために勝利の確率の推定値を受け取ります。 前述のように、この評価は、同じミニマックスアルゴリズムの起動で構成されますが、他の状態では、すでに別のプレーヤーの動きがあり、既に最大化ではなく最小化が行われています。 これはすでに2番目のレベルで、指定された深さ1の最後のレベルになります。それ以降、ミニマックスアルゴリズムは開始されませんが、ヒューリスティック評価関数を返します。

この例は、下から見ると理解しやすくなります。 2番目のレベルでは、ヒューリスティック推定値を取得する状態があります（数値で記述されています）。 2番目のレベルでは、最初のレベルがそれぞれ等級を取得し、次のレベルでチェックされるものから最小値を選択します。 まあ、ゼロレベルは、最初のレベルによって彼に与えられたものから、最大評価を選択します。

すべての評価が得られたので、どうすればよいですか？ 喜ぶ。 移動を選択する必要があります。 ここではすべてが明らかです。オオカミにとっては最高のスコアを示すものが動きを選択し、ノウサギにとっては最低のスコアを示すものが選択されます。 しかし、異なる動きの推定値は等しくなる可能性があり、理想的にはランダムに選択する必要がありますが、ここで微妙な違いが始まります。 私は、オオカミに対しては最大のマークを持つリストからの最初の動きが取られ、ウサギにとっては、最も低いマークを持つリストからの最後の動きが取られるとすぐに言わなければなりません。 かなり深刻な最適化は、目的のリストからの最初の移動が常に選択されるという事実に依存しているため、これは悲しいことです。 しかし、うさぎにとっては、これはまったく不適切です。 事実は、オオカミは非常に頻繁に（可能な限り）歩き、スコアが無限（254）に等しくなるため、うさぎの動きが「意味のない」ものになり、動きを選択した場合、彼は下に移動します。 、そして我々は彼を前進させ、狼の前線を壊さなければなりません。 ヒューリスティック関数にノウサギの高さを考慮させるのは正しいことですが、メインヒューリスティックよりも低い係数ですが、既に説明したようにそれを行いませんでした。 したがって、リストから最後の動きが選択され、ウサギに上昇するよう指示されます。

アルゴリズムの実装例：

  //    f(Vi) int Game::runMinMax(MonsterType monster, int recursiveLevel) { int test = NOT_INITIALIZED; //    ( )     if (recursiveLevel >= this->AILevel * 2) return getHeuristicEvaluation(); //  . 0-7 -   , 8-11 -    int bestMove = NOT_INITIALIZED; bool isWolf = (monster == MT_WOLF); int MinMax = isWolf ? MIN_VALUE : MAX_VALUE; //      for (int i = (isWolf ? 0 : 8); i < (isWolf ? 8 : 12); i++) { int curMonster = isWolf ? i / 2 + 1 : 0; QPoint curMonsterPos = curMonster == 0 ? rabbit : wolfs[curMonster - 1]; QPoint curMove = possibleMoves[isWolf ? i % 2 : i % 4]; if (canMove(curMonsterPos + curMove)) { //...,     temporaryMonsterMovement(curMonster, curMove); //,   ,    test = runMinMax(isWolf ? MT_RABBIT : MT_WOLF, recursiveLevel + 1); //   ,     - ,    if ((test > MinMax && monster == MT_WOLF) || (test <= MinMax && monster == MT_RABBIT)) { MinMax = test; bestMove = i; } //...     temporaryMonsterMovement(curMonster, -curMove); } } if (bestMove == NOT_INITIALIZED) return getHeuristicEvaluation(); //  , ,      if (recursiveLevel == 0 && bestMove != NOT_INITIALIZED) { if (monster == MT_WOLF) wolfs[bestMove / 2] += possibleMoves[bestMove % 2]; else rabbit += possibleMoves[bestMove % 4]; } return MinMax; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

注意！ ここで、bestMove変数は多くの意味をカプセル化しています（要求に応じて指定します）。すべてを正しく実行していることがわからない場合は、4ビットにあまり意味を投資しないことをお勧めします。

リテラシーと教育を受けた人々であるあなたは、決定木がある場所には最適化のための宝物もあることをすでに推測しました。 この例も例外ではありません。

アルファベータクリッピング

アルファベータクリッピングは、一部の動きの分析を予定より早く停止できるという考えに基づいており、証言の結果を無視します。 アルファベータクリッピングは、しばしば別のアルゴリズムとして説明されますが、これは受け入れられないと考え、最適化の修正として説明します。 アルファベータは、ブランチメソッドおよびバインドメソッドのクラスに属します。

大まかに言えば、最適化は2つの追加変数alphaおよびbetaを導入します。alphaは、最大化プレーヤー（オオカミ）が選択しない現在の最大値であり、 betaは最小化プレーヤー（うさぎ）が選択しない現在の最小値です。 最初は、それぞれ-∞、+∞に設定され、推定値を取得するとf（Vi）が変更されます。

• alpha = max（alpha、f（Vi））; 最大化のレベル。
• beta = min（ベータ、f（Vi））; 最小化のレベル。

条件alpha> betaが真になり、それが期待の矛盾を意味するとすぐに、Vikの分析を中断し、このレベルの最後に受け取った推定値を返します。

この例の2番目の図では、アルファとベータのカットオフを使用して、下の3行が完全に切り取られていますが、左端の列はありません。 これは説明の良い例ではないと思うので、ウィキペディアの例を取り上げます。


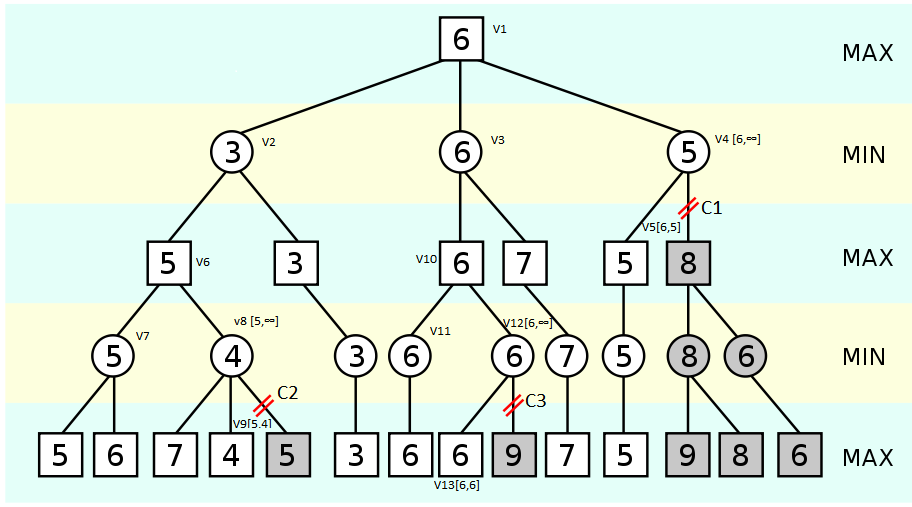
例の指定：

• Viは決定ツリーのノードであり、iはツリートラバーサルの順序とはまったく関係ありません。
• Vi [アルファ、ベータ]-アルファ、ベータの指定された現在値を持つノード。
• Ciはi-alphaアルファクリッピングです。
• MIN、MAX-それぞれ最大化と最小化のレベル。 最大レベルの状態は、MINが示されている次のレベルの状態から最大値を選択することに注意してください。逆も同様です。 つまり、最大値はMINが書き込まれたものから選択され、MAXが書き込まれたもののうちの最小値は混同しないでください。

クリッピング1を検討します。ノードV3のバリアントがノードV1に対して完全に処理され、その推定値f（V3）= 6が取得された後、アルゴリズムはこのノード（V1） 。 ここで、V4のすべての子ノードの最小アルファ=6。V4ノードがV5ノードでバリアントを処理し、推定f（V5）= 5を受け取った後、アルゴリズムはV4ノードのベータ値を調整します。 更新後、V4ノードの場合、alpha> betaという状況が発生したため、V4ノードの他のオプションは不要です。 そして、カットオフノードのグレードは関係ありません。

• クリップされたノードの値が5（ベータ）以下の場合、ノードV4で5以下の推定値が選択されます。したがって、ノードV3の評価が優れているため、ノードV4のオプションはノードV1で選択されることはありません。
• クリップされたノードの値が6（ベータ+ 1）以上の場合、V4ノードは評価が低い（より良い）ため、V5ノードのオプションを選択するため、ノードはそれ以上考慮されません。

Clipping 2の構造はまったく同じです。自分で分解することをお勧めします。 クリッピング3は、はるかに興味深い注意です 。Wikipediaの例は明らかに間違っています。 （alpha> = beta）の場合、彼はクリッピングを実行できますが、alpha-betaは最適化であり、パスの選択には影響しません。 実際には、一般的なケースではalpha> betaの場合にのみ、alpha> = betaの場合にクリッピングが機能するはずであると書いています。

ある決定木について、すべての子供が同じスコアを表示するとします。 その後、ランダムにそれらのいずれかを選択できますが、それは正しいでしょう。 ただし、alpha> = betaの条件を使用してこれを行うことはできません。これは、最初の評価の後、他のすべてを遮断できるためです。 しかし、それは重要ではありません。たとえば、アルゴリズムは確率的動作を実装しません。これはそれほど重要ではありませんが、アルゴリズムで同じ評価の最適な値の選択が重要である場合、このクリッピング条件によりアルゴリズムが単純に壊れてしまいます最適ではありません。 警戒してください！

アルファベータクリッピングは、実装するのが非常に簡単なアルゴリズムであり、その本質は、ミニマックス関数では、推定を受け取った直後に、ミニマックスプロシージャのインターフェイスに2つの変数alphaとbetaを追加し、その本体に小さなコードを追加する必要があるという事実に要約されます

アルファベータクリッピングを使用してミニマックスアルゴリズムを変更する例（明確にするために、変更はコメント化されていますが、これは重要なコードであり、コメントではないことに注意してください）：

 int Game::runMinMax(MonsterType monster, int recursiveLevel/*, int alpha, int beta*/) { int test = NOT_INITIALIZED; if (recursiveLevel >= this->AILevel * 2) return getHeuristicEvaluation(); int bestMove = NOT_INITIALIZED; bool isWolf = (monster == MT_WOLF); int MinMax = isWolf ? MIN_VALUE : MAX_VALUE; for (int i = (isWolf ? 0 : 8); i < (isWolf ? 8 : 12); i++) { int curMonster = isWolf ? i / 2 + 1 : 0; QPoint curMonsterPos = curMonster == 0 ? this->rabbit : this->wolfs[curMonster - 1]; QPoint curMove = this->possibleMoves[isWolf ? i % 2 : i % 4]; if (canMove(curMonsterPos + curMove)) { temporaryMonsterMovement(curMonster, curMove); test = runMinMax(isWolf ? MT_RABBIT : MT_WOLF, recursiveLevel + 1, alpha, beta); temporaryMonsterMovement(curMonster, -curMove); if ((test > MinMax && monster == MT_WOLF) || (test <= MinMax && monster == MT_RABBIT)) { MinMax = test; bestMove = i; } /* if (isWolf) alpha = qMax(alpha, test); else beta = qMin(beta, test); if (beta < alpha) break; */ } } if (bestMove == NOT_INITIALIZED) return getHeuristicEvaluation(); if (recursiveLevel == 0 && bestMove != NOT_INITIALIZED) { if (monster == MT_WOLF) this->wolfs[bestMove / 2] += this->possibleMoves[bestMove % 2]; else this->rabbit += this->possibleMoves[bestMove % 4]; } return MinMax; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

前に言ったように、アルファベータクリッピングは非常に効果的であり、次の指標がこれを証明しています。 それぞれの場合について、計算の深さの3つの異なるレベルで、ヒューリスティック評価関数への入力の数を測定しました（少ない方が良い）。

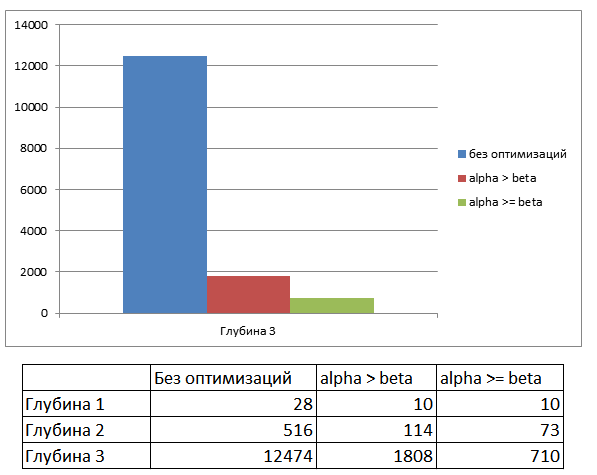
結論として、このクリッピングアルゴリズムの使用は、知性の仕事を加速するだけでなく、そのレベルも向上させると言えます。

ニュアンス

アルゴリズムは、相手が最適に考える場合にのみ最適な動きをします。 ストロークの品質は、主に再帰の深さとヒューリスティックの品質に依存します。 ただし、このアルゴリズムは移動の品質を非常に深く評価し、（ヒューリスティックで明示的に記述されていない限り）移動の数に結び付けられないことに注意してください。 言い換えれば、このアルゴリズムを追加の変更なしでチェスに適用すると、チェックメイトが遅くなります。 そしてこの例では、オオカミの最適な戦略で勝つ方法がないことをノウサギが理解した場合、損失を遅らせることができるという事実にもかかわらず、彼は自殺することができます。

繰り返しますが、alpha> = betaをalpha betaのクリッピング条件にしないでください。これが実装に受け入れられることを100％確信していない限り。 それ以外の場合、アルファベータ版は、アルゴリズム全体の知能を高い確率で低下させます。

このアルゴリズムは、多数の異なる変更の基盤であるという意味で基本的です。 ここに示されている形式では、チェッカー、チェス、ゴーには使用できません。 ほとんどの変更は以下を求めます：

• 計算を再利用します。
• 深さの異なるさまざまな状況を分析する
• 特定のゲームの一般的な原則と経験則により、カットオフの数を増やします。
• 移動パターンを実装します。 たとえば、チェスでは、最初のいくつかの動きはオープニングであり、ミニマックス作業ではありません。
• 移動のサードパーティの品質尺度を実装します。 たとえば、1回の移動で勝つことができるかどうかを確認し、可能であれば、ミニマックスを起動せずに勝つことです。
• はるかに。

膨大な数の変更により、コンピューターでチェスをしたり、人を倒したりすることができます。 そのような変更がなければ、ミニマックスは、現代のスーパーコンピューターであっても、チェスには実際には適用できません。 最適化なしでは、3つの動きのチェスでは、約30 ^ 6の動き（729億）をチェックする必要があり、より深い計算の深さが必要です...

ハッピーエンド

約束どおり- ソース 、 Windows用バージョン （つるで動作するはずです）。 チェッカー、チェスにも同じように書くことをお勧めします-便利です。