インターネットとゲームがブラウザで結合され始めたときが来ました(フラッシュはカウントされません)。
ブラウザゲームには多くの例がありますが、そのほとんどはカジュアルゲームですが、オタクにとってアクション、RTSおよびRPGのジャンルはより興味深いものであり、開発者にとってはその実装です。
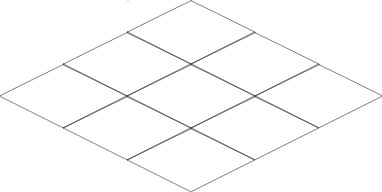
RTS、RPGジャンル、ターンベースの戦略では、マトリックスはユニットの移動、テクスチャの描画などの主要なメカニズムです。 しかし、マトリックスとアイソメトリックテクスチャを組み合わせようとすると、地獄になってしまいます。このマトリックスを制御して影響を与えるレイヤーを書くまで、そこから抜け出すことはできません。
カットの下で私は言います:
- 等尺性マトリックスの描画方法
- フルスクリーン等尺性マトリックスを描画する方法
はじめに
通常の正方行列を描くのは非常に簡単で、対称的であり、座標の検索は一般に難しい作業ではありませんが、等尺性行列は作業に2つの修正を導入します。
- マトリックスの描画は、キャンバスの中央から行う必要があります。
- レンダリングの錯視。
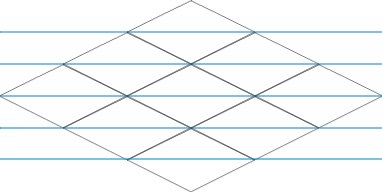
これらの問題はすべて、実装中に考慮する必要があります。
マトリックスレンダリング
等尺性マトリックスの機能の最初の段落で述べたように、レンダリングはキャンバスの中央から行われる必要があります。 そのため、キャンバスの中央が必要です。
2番目の段落では、視覚的な欺ceptionに注意を払う必要があります。 脳は画像を見て、それを水平に描きたいのですが、次の画像に示すように、斜めに描く必要があります。
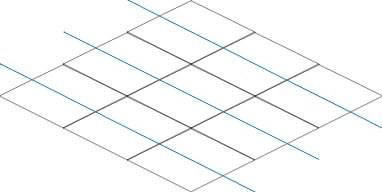
すでに最も基本的な問題を検討しましたので、実装を見てみましょう。
すべてコメント化されており、実用的な例がありますので、自分ですべてを見ることができます。
レンダリングの実装
var element = document.getElementById('canvas'); element.width = 1024; element.height = 512; var ctx = element.getContext('2d'); var image = new Image(); image.src = 'http://habrastorage.org/storage2/e61/42d/5b2/e6142d5b26d171611d60d5941e390398.png'; // var width = 128; var height = 64; image.onload = function() { function draw(x, y) { ctx.drawImage(image, x - width / 2, y - height / 2, width, height); } // X Y . // , // , . var Xo = 0; var Yo = 0; // var C = Math.floor(element.width / 2); // X, // Y var Xc = 0; var matrixHeight = 8; var matrixWidth = 8; for(var y = 0; y < matrixHeight; y++) { // , Yo = (height / 2) * y; // . Xc = C - (width / 2 * y); for(var x = 0; x < matrixWidth; x++) { // X . // , . // Xo = Xc + (x * (width / 2)); // Y. // X, // X, Y. Yo += height / 2; draw(Xo, Yo); } } }
これが既製の例です
フルスクリーンマトリックスレンダリング
さて、アイソメトリックマトリックスを描画できましたが、今度はフルスクリーンで描画する必要があります。
それをもう少し複雑に、またはむしろ:
- 総マトリックスシフト高さを計算する
- 空の領域を埋めるために、マトリックスの追加の高さと幅を計算する必要があります。
- 不可視領域のレンダリングに制限を設定する
総マトリックスシフト高さの計算の理論と実践
実際には、標準マトリックスを描画するとき、三角形の形の空の領域が得られます。
つまり、未知の辺を計算し、その高さでシフトを行うことができ、穴が残らないようにします。
私たちは片足の長さを知っており、低血圧の長さを簡単に見つけることができます。
辺Aは既知の脚の長さです(レンダリング領域全体の幅を2で割った値)。 つまり 1024px / 2 = 512px、脚の長さA
サイドB-この区間はわかりません。計算する必要があります。
Side C-Hypotenuse、その長さを調べるには、小さな菱形の辺の1つの長さを計算する必要があります。
これを行うには、ひし形の幅と高さの半分を取り、それらを正方形にまとめて集計し、結果の平方根を計算します。
... var width = 128; var height = 64; var grainLength = Math.sqrt((width / 2) * (width / 2) + (height / 2) * (height / 2)); // 71.554 // , 64px 128px image.onload = function() { ...
菱形の1つのファセットの長さを計算したら、キャンバスの幅の半分を32で除算し、結果に菱形のファセットの長さを掛ける必要があります。
... var grainLength = Math.sqrt((width / 2) * (width / 2) + (height / 2) * (height / 2)); var center = Math.floor(element.width / 2); var hypotenuse = center / (width / 2) * grainLength; image.onload = function() { ...
次に、有名な脚と斜辺を正方形に入れます。 斜辺から脚を引き、結果の平方根を計算します。
... var hypotenuse = center / (width / 2) * grainLength; var catheusA = center * center; hypotenuse *= hypotenuse; // , . var catheusB = Math.sqrt(hypotenyse - catheusA); image.onload = function() { ...
それだけです、方程式は解かれましたが、レンダリング計算に結果を適用するために残っています。
... for(var y = 0; y < matrixHeight; y++) { Yo = (height / 2) * y; Xc = C - (64 * y); ...
この例からわかるように 、今度は菱形を描画して、上部に穴がないようにします。
しかし今、問題番号2があります。 領域の追加の高さと幅を計算する必要があります。
これを行うのは難しくありませんが、今度は静的に指定されたマトリックスの幅または高さを放棄します。
幅が高さよりも大きい場合は、幅を32で除算する必要があります。それ以外の場合は高さ
... var matrixHeight = (element.width > element.height ? element.width : element.height) / 32; var matrixWidth = (element.width > element.height ? element.width : element.height) / 32; ...
さて、私が言ったように、3つ目の問題があります。 キャンバスの外側の領域を描画しようとしています。
キャンバスの幅と高さの通常の条件によってこれを制限できますが、画像の幅と高さをさらに増やすと、
空の領域がないように。
... Xo = Xc + (x * 64); Yo += 32; if(Xo < (width / -1) || Xo > element.width + width || Yo < (height / -1) || Yo > element.height + height) continue; draw(Xo, Yo); ...
以上です。 完全な例です。 これで、本格的な等尺性マトリックスの描画方法を学習しましたが、これはストーリーの半分にすぎません。
マトリックス内のエントリを見つけることはより困難になります。 クリックされたマトリックス座標を計算し、座標が呼び出された場合、この座標の中心がどこにあるかを計算します。 しかし、それについては次の記事で詳しく説明します。